Significado de fracciones equivalentes Definición, ejemplos, amplificación, simplificación y fracción irreducible

Licenciada en Física
Definición formal
Una fracción equivalente es el contraste de dos o más fracciones que representan una misma cantidad.
Por ejemplo, al dividir una pizza en cuatro partes iguales, \(\frac{1}{2}\) de ella equivale exactamente a sus \(\frac{2}{4}\) partes, por lo tanto las fracciones \(\frac{1}{2}\) y \(\frac{2}{4}\) son equivalentes.

Del mismo modo, \(\frac{3}{4}\) partes de pizza equivalen a \(\frac{6}{8}\) partes de la misma, por lo tanto ambas fracciones también son equivalentes y expresan la misma cantidad de pizza.
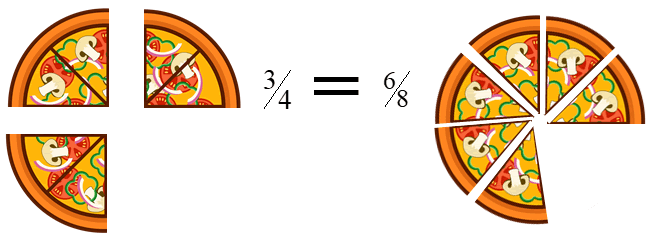
Por su parte, se pueden obtener fracciones equivalentes a una determinada fracción mediante amplificación o simplificación, tal como se ejemplifica en las línes de este texto.
¿Cómo saber si dos fracciones son equivalentes?
Siempre se expresa la misma cantidad. Como una fracción \(\frac{a}{b}\) es la manera de expresar el cociente entre a y b sin resolverlo explícitamente, una manera de averiguar si dos fracciones son equivalentes es mostrar el valor de este cociente en números decimales.
Por ejemplo: \(\frac{1}{2}=0.5\) y \(\frac{2}{4}=0.5\). De esta forma se puede asegurar que las fracciones son equivalentes.
Pero hay un procedimiento para verificar la equivalencia de fracciones en el que no es necesario dividir numerador y denominador.
Se trata de los productos cruzados o multiplicación en cruz, en los cuales el numerador de una de las fracciones se multiplica con el denominador de la otra, y luego el denominador de la primera se multiplica con el numerador de la otra. Si los productos cruzados dan igual resultado, se puede asegurar que las fracciones son equivalentes.
Esto se puede expresar abreviadamente, suponiendo que se tienen dos fracciones cualesquiera \(\frac{a}{b}\) y \(\frac{c}{d}\). Se afirma que son equivalentes si:
a×d = b×c
Por ejemplo, las fracciones \(\frac{3}{4}\)y \(\frac{6}{8}\) son equivalentes, ya que:
3×8 = 6×4 = 24
En cambio, las fracciones \(\frac{2}{5}\) y \(\frac{3}{7}\) no son equivalentes, puesto que:
2×7=14
3×5=15
Ejemplo 1: Indicar si los siguientes pares de fracciones son equivalentes o no
a) \(\frac{3}{4}\)y \(\frac{{21}}{{28}}\)
b) \(\frac{2}{9}\)y \(\frac{9}{{22}}\)
Respuestas
a) Se resuelven los productos cruzados:
3×28 = 84
4×21 = 84
Como son iguales, se concluye que las fracciones son equivalentes.
b) Con el mismo procedimiento:
2×22 = 44
9×9 = 81
Dado que los productos son diferentes, las fracciones no son equivalentes.
Amplificación de fracciones
Consiste en multiplicar el numerador y el denominador de una fracción por un mismo número diferente de 0 y de 1, de esta manera, variando el número, se obtienen fracciones equivalentes a la fracción dada.
Ejemplo 2: Obtener tres fracciones equivalentes a la fracción \(\frac{2}{5}\) por amplificación.
Respuesta. Se multiplican numerador y denominador de la fracción dada por un número escogido arbitrariamente:
-Multiplicando por 2:
\(\frac{2}{5}=\frac{{2\times 2}}{{5\times 2}}=\frac{4}{{10}}\)
-Por 3:
\(\frac{2}{5}=\frac{{2\times 3}}{{5\times 3}}=\frac{6}{{15}}\)
-Y por 4:
\(\frac{2}{5}=\frac{{2\times 4}}{{5\times 4}}=\frac{8}{{20}}\)
De manera que las fracciones \(\frac{\text{2}}{\text{5}}\text{, }\frac{\text{4}}{{\text{10}}}\text{, }\frac{\text{6}}{{\text{15}}}\text{y }\frac{\text{8}}{{\text{20}}}\)son todas equivalentes.
Simplificación de fracciones
Dada una fracción cualquiera, si se divide numerador y denominador por un mismo número diferente de 0 y de 1, se obtiene una fracción equivalente a la fracción dada, siempre y cuando el numerador y el denominador sean múltiplos del número seleccionado.
Ejemplo 3: Obtener 3 fracciones equivalentes a \(\frac{{40}}{{100}}\) mediante simplificación
Respuesta. Los números 40 y 100 son múltiplos de 2 (por ser pares ambos) y de 5 y de 10 (porque los dos terminan en 0), así que se pueden obtener tres fracciones equivalentes dividiendo numerador y denominador por dichos números:
\(\frac{{40}}{{100}}=\frac{{40\div 2}}{{100\div 2}}=\frac{{20}}{{50}}\)
\(\frac{{40}}{{100}}=\frac{{40\div 5}}{{100\div 5}}=\frac{8}{{20}}\)
\(\frac{{40}}{{100}}=\frac{{40\div 10}}{{100\div 10}}=\frac{4}{{10}}\)
De esta manera, las fracciones \(\frac{{\text{40}}}{{\text{100}}}\text{, }\frac{{\text{20}}}{{\text{50}}}\text{, }\frac{\text{8}}{{\text{20}}}\text{ y }\frac{\text{4}}{{\text{10}}}\), son todas equivalentes.
La fracción irreducible
Supone la fracción equivalente más simple de todas a una fracción dada. En el ejemplo anterior, se encontraron tres fracciones equivalentes a \(\frac{{40}}{{100}}\), de las cuales \(\frac{4}{{10}}\) tiene los números más pequeños, pero no es la más simple de todas, puesto que 4 y 10 son números pares y aún se admite otra fracción equivalente, dividiendo numerador y denominador entre 2:
\(\frac{4}{{10}}=\frac{{4\div 2}}{{10\div 2}}=\frac{2}{5}\)
El numerador y el denominador de esta fracción son números primos entre sí, de modo que no hay otro número, aparte del 1, que los divida a ambos exactamente. Por lo tanto, esta es la fracción más simple de todas las fracciones equivalentes a \(\frac{{40}}{{100}}\).
Trabajar con las fracciones irreducibles es muy conveniente, ya que de este modo se trabaja con números más pequeños, los cuales resultan siempre más manejables.
Pasos para hallar la fracción irreducible
Para hallar la fracción irreducible de una fracción dada se procede del siguiente modo:
-Descomponer el numerador y el denominador en sus factores primos.
-Hallar el máximo común divisor (MCD), que es el producto de los factores que tengan en común, tomados con su menor exponente.
-Dividir numerador y denominador entre este divisor.
Ejemplo 4: Hallar la fracción irreducible de \(\frac{{54}}{{204}}\)
Respuesta. En términos de sus factores primos, el numerador y el denominador de la fracción se expresan mediante:
54 = 33×2
204 = 17×22×3
Los factores comunes en ambos números son el 2 y el 3, que al ser tomados con su menor exponente y multiplicados resulta:
2×3 = 6
Por lo tanto:
\(\frac{{54}}{{204}}=\frac{{54\div 6\,}}{{204\div 6}}=\frac{9}{{34}}\)
La fracción irreducible buscada es \(\frac{9}{{34}}\).

Trabajo publicado en: Ene., 2021.