Definición de Función Exponencial

Maestría en Matemáticas, Dr. en Ciencias
La función exponencial modela varios fenómenos naturales y situaciones sociales y económicas, es por lo que es importante identificar las funciones exponenciales en diversos contextos.
Recordemos que para un número se define \({a^1} = a,{a^2} = aa,\;{a^3} = aaa\), en general se tiene que para cualquier \(n\) número natural:
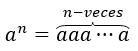
En caso de que \(a \ne 0\), se tiene que: \({a^0} = 1,\;\) en efecto, cuando \(a \ne 0,\) tiene sentido hacer la operación \(\frac{a}{a} = 1;\) al aplicar la ley de los exponentes, se tiene:
\(\frac{a}{a} = 1\)
\({a^{1 – 1}} = 1\)
\({a^0} = 1.\)
Cuando \(a = 0\), el razonamiento anterior no tiene sentido, por lo cual, la expresión \({0^0},\) carece de interpretación matemática.
En caso de que \(b > 0\) y se cumpla que \({b^n} = a,\) se dice que \(b\) es la enésima raíz de \(a\) y suele denotarse como \(b = {a^{\frac{1}{n}}},\;\) o \(b = \sqrt[n]{a}\).
Cuando \(a < 0\), no existe un número real \(b\) tal que \({b^2} = a;\) debido a que \({b^2} \ge 0;\;\) así que expresiones de la forma \({a^{\frac{m}{n}}}\), no serán consideradas para \(a < 0.\) En la siguiente expresión algebraica: \({a^n}\) \(a\) es llamado base, y \(n\) es llamado exponente, \({a^n}\)es llamada la potencia\(\;n\) de \(a\) o también es llamada \(a\) a la potencia \(n,\;\)se cumplen las siguientes leyes de los exponentes:
| \({a^n}{a^m} = {a^{n + m}}\) | \(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\) | \({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\) |
|---|---|---|
| \(\frac{1}{{{a^n}}} = {a^{ – n}}\) | \({a^n} = \frac{1}{{{a^{ – n}}}}\) | \({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\) |
| \({\left( {ab} \right)^n} = {a^n}{b^n}\) | \({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1}{n}}} = {a^{\frac{m}{n}}}\) | \({a^0} = 1\) para cada \(a \ne 0\) |
La función exponencial es de la forma:
\(f\left( x \right) = {a^x}\)
donde \(a > 0\) es una constante y la variable independiente es el exponente \(x\).
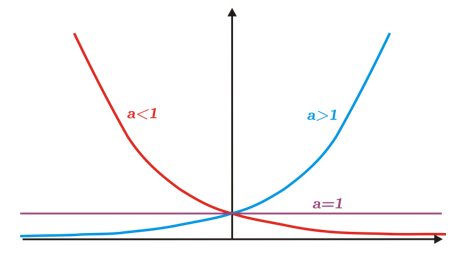
Para hacer un análisis de la función exponencial, consideraremos tres casos
Caso 1 Cuando la base \(a = 1.\)
En este cas0, \(a = 1,\) la función \(f\left( x \right) = {a^x}\) es una función constante.
Caso 2 Cuando la base \(a > 1\)
En este caso, se tiene lo siguiente:
| Valor de \(x\) | |
|---|---|
| \(x < 0\) | \(0 < {a^x} < 1\) |
| \(x = 0\) | \({a^0} = 1\) |
| \(0 < x < 1\) | \(1 < {a^x} < a\) |
| \(x = 1\) | \({a^x} = 1\) |
| \(x > 1\) | \(a < {a^x}\) |
La función \(f\left( x \right) = {a^x}\) es una función estrictamente creciente, es decir, si \({x_2} > {x_1}\), entonces:
\({a^{{x_2}}} > a_{}^{{x_2}}\)
\(f\left( {{x_2}} \right) > f\left( {{x_1}} \right)\)
Cuando un fenómeno se modela con una función exponencial, con \(a > 1\), decimos que presenta un crecimiento exponencial.
Caso 2 Cuando la base \(a < 1\).
| Valor de \(x\) | |
|---|---|
| \(x < 0\) | \({a^x} > 1\) |
| \(x = 0\) | \({a^0} = 1\) |
| \(0 < x < 1\) | \(0 < {a^x} < 1\) |
| \(x = 0\) | \({a^x} = 1\) |
| \(x > 1\) | \(0 < {a^x} < a < 1\) |
Cuando \(a < 1\), la función \(f\left( x \right) = {a^x}\) es una función estrictamente de decreciente, es decir, si \({x_2} > {x_1}\), entonces:
\({a^{{x_2}}} < a_{}^{{x_1}}\)
\(f\left( {{x_2}} \right) < f\left( {{x_1}} \right)\)
Cuando un fenómeno se modela con una función exponencial, con \(a < 1\), decimos que presenta un decaimiento o decrecimiento exponencial.
La siguiente gráfica ilustra el comportamiento de \({a^x}\), en sus tres diferentes casos.
Aplicaciones de la función exponencial
Ejemplo 1 Crecimiento Poblacional
Denotaremos con \({P_0}\) es la población inicial y con \(r \ge 0\) a la tasa de crecimiento de población, si la tasa de población se mantiene constante durante el tiempo; la función
\(P\left( t \right) = {P_0}{\left( {1 + r} \right)^t};\)
calcula la población que hay en el tiempo t.
Ejemplo práctico 1
La población de México, en el año 2021 es de 126 millones y presentó un crecimiento anual del 1.1%, en caso de mantenerse dicho crecimiento, ¿Qué población habrá en México en el año 2031, en el año 2021?
Solución
En este caso \({P_o} = 126\) y \(r = \frac{{1.1}}{{100}} = 0.011\), por lo cual se debe de usar:
\(P\left( t \right) = {P_0}{\left( {1 + .0011} \right)^t}\)
La tabla siguiente muestra los resultados
| Año | Tiempo transc. (\(t\)) | Cálculo | Población (Millones) |
|---|---|---|---|
| 2021 | 0 | \(P\left( t \right) = 126{\left( {1.0011} \right)^0}\) | 126 |
| 2031 | 10 | \(P\left( t \right) = 126{\left( {1.0011} \right)^{10}}\) | 140.57 |
| 2051 | 30 | \(P\left( t \right) = 126{\left( {1.0011} \right)^{30}}\) | 174.95 |
Ejemplo 2 Cálculo de intereses compuestos
Los bancos ofrecen una tasa de interés anual, pero la tasa real, depende a cuántos meses lo inviertas; por ejemplo, si te ofrecen la tasa de interés de r% anual, la tasa real mensual es de \(\frac{r}{{12}}\)%, la bimestral es de \(\frac{r}{6}\)%, la trimestral es \(\frac{r}{4}\)%, la cuatrimestral es del \(\frac{r}{3}\)%, y la semestral es de \(\frac{r}{2}\)%.
Ejemplo práctico 2
Supongamos que inviertes 10,000 en un banco y te ofrecen las siguientes tasas de interés anuales:
| Depósitos a plazo fijo | Tasa anual | Períodos en un año | Tasa real | Dinero acumulado en \(k\) meses |
|---|---|---|---|---|
| De dos meses | 0.55% | 6 | \(\frac{{0.55\% }}{6} = 0.091667{\rm{\% }}\) | \(10000{\left( {1 + 0.00091667} \right)^{\frac{k}{2}}}\) |
| De tres meses | 1.87% | 4 | \(\frac{{1.87\% }}{4} = 0.4675{\rm{\% }}\) | \(10000{\left( {1 + 0.00461667} \right)^{\frac{k}{3}}}\) |
| De seis meses | 1.56% | 2 | \(\frac{{1.56\% }}{4} = 0.78{\rm{\% }}\) | \(10000{\left( {1 + 0.0078} \right)^{\frac{k}{6}}}\) |
El número \(e\), constante de Euler y el interés continuo.
Ahora supongamos que tenemos un capital inicial \(C\) y lo invertimos una tasa fija \(r > 0\), y dividimos el año en \(n\) períodos; el capital acumulado en un año es igual a:
\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)
Para analizar cómo se comporta el capital acumulado cuando \(n\),crece, para ello reescribiremos el capital acumulado, en un año:
\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)\(A = \;C{\left( {1 + \frac{1}{{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right)r}},\)
haciendo \(m = \frac{n}{r}\), se obtiene:
\(A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}\)\(A = C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r}.\)
A medida que \(n\) crece también lo hace \(m = \frac{n}{r}.\)
A medida que \(m = \frac{n}{r},\) crece la expresión \({\left( {1 + \frac{1}{m}} \right)^m}\)se aproxima a lo que se llama la constante o número de Euler:
\(e \approx 2.718281828 \ldots .\)
La constante de Euler no tiene expresión decimal finita, ni periódica.
Tenemos las siguientes aproximaciones
\(C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \approx C{e^r},\)\(C{\left( {1 + \frac{r}{n}} \right)^{ns}} \approx C{e^{rs}}.\)
A la expresión:
\(A = \;C{e^r},\)
la podemos interpretar de dos maneras:
1.- Como la cantidad máxima que podemos acumular en un año cuando invertimos un capital \(C,\;\)a una tasa anual \(r.\)
2.- Como la cantidad que acumularíamos, en un año, si nuestro capital se reinvirtiera de manera continua a una tasa anual \(r.\)
\(T\left( s \right) = \;C{e^{rs}},\)
es la cantidad acumulada si se invierte \(s\) años con interés continuo.
Ejemplo concreto 3
Ahora retomaremos una parte del ejemplo concreto 2, donde la tasa anual es 0.55% a plazos bimestrales. Calcular el capital que se acumula si se el capital inicial es del 10000 y se reinvierte medio año, dos años, 28 meses.
\(10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525\)
como muestra la siguiente tabla, el valor de \(m = \frac{n}{r},\) no es “pequeño” y la tabla anterior indica que \({\left( {1 + \frac{1}{m}} \right)^m}\) es cercano a la constante de Euler.
| Tiempo | Número de periodos (\(k\)) | Capital acumulado, en miles, reinvertido cada dos meses |
|---|---|---|
| Medio año | 3 | \(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\) |
| Dos años | 12 | \(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\) |
| 38 meses | 19 | \(10{\left( {1.00091667} \right)^{19}} = 10.\;175612\) |
| Tiempo | Tiempo de años (\(s\)) | Capital acumulado, en miles, invertirlo con interés continuo |
|---|---|---|
| Medio año | \(s = \frac{1}{2}\) | \(10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\) |
| Dos años | \(s = 2\) | \(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\) |
| 38 meses | \(s = \frac{{19}}{6}\) | \(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\) |
Ejemplo 2 Depreciación
Ejemplo práctico 1
Una computadora se deprecia un 30% cada año, si una computadora costó $20000 pesos, determina el precio de la computadora para \(t = 1,12,\;14,\;38\) meses.
En este caso, se tiene:
\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0.30} \right)^t}\)
Con \(t\) en años, al sustituir \(t\) en la siguiente tabla se obtiene
| Tiempo en meses | Tiempo en años | Cálculos | Valor numérico |
|---|---|---|---|
| 1 | \(\frac{1}{{12}}\) | \(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\) | 19414.289 |
| 12 | 1 | \(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\) | 14000 |
| 14 | \(\frac{7}{6}\) | \(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\) | 13192.012 |
| 38 | \(\frac{{19}}{6}\) | \(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\) | 6464.0859 |

Trabajo publicado en: Nov., 2022.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.