Definición de Logaritmo

Maestría en Matemáticas, Dr. en Ciencias
1. Expresión matemática que representa el número de veces que se debe multiplicar un número A (base) por un número B (exponente) para obtener el número C, formulando la ecuación: Aᴮ = C.
Etimología: por el latín científico logarithmus, definido como tal en 1614 por el matemático escocés John Napier (1550-1617), en su trabajo Mirifici logarithmorum canonis descriptio (que se puede traducir a Descripción del maravilloso canon de los logaritmos). Construido sobre las referencias del griego λόγος (lógos), utilizado de forma recurrente como sufijo -λογία (-logía), en cuanto ‘ciencia’, ‘palabra’, y en este caso en particular ‘razón’, y ἀριθμός (arithmós), para remitir a ‘número’, como en artitética, en el latín arithmetĭca, respecto del griego ἀριθμητική (arithmētikḗ).
Cat. gramatical: Sustantivo masc.
En sílabas: lo-ga-rit-mo.
Logaritmo
A instancias de las matemáticas, un logaritmo es el exponente al cual es necesario elevar a una determinada cantidad positiva para que resulte un número determinado. También se lo conoce como la función inversa a la función exponencial. En tanto, se denomina logaritmación a la operación matemática a través de la cual, dando un número resultante y una base de potenciación se tendrá que hallar el exponente al cual habrá que elevar la base para así conseguir el mencionado resultado. Tal como sucede con la suma y la multiplicación que tienen sus operaciones opuestas, la división y la resta, la logaritmación tiene a la exponenciación como su función inversa. Ejemplo: 102 = 100, el logaritmo de 100 en base 10 será el 2 y se lo escribirá de la siguiente forma: log100 = 2.
Este método de cálculo a través de los denominados logaritmos fue impulsado por John Napier a comienzos del siglo XVII. El método logarítmico no solamente contribuyó en cuanto al avance de la ciencia sino que además se convirtió en una herramienta fundamental en el ámbito de la Astronomía haciendo más simples cálculos realmente muy complejos. A los logaritmos se los usó muchísimo en la geodesia, en algunas ramas de la matemática aplicada y en la navegación marítima cuando las calculadoras y las computadoras todavía no eran el hecho concreto que son hoy en día.
Avanzamos sobre situaciones que se pueden observar en la vida real para comprender la relevancia de los logaritmos, y luego analizamos los principios sobre los cuales se rigen y los modos de graficarlos.
Ejemplo práctico 1 en finanzas
Un Banco ofrece una tasa anual al 7% de interés anual compuesto, capitalizable cada mes. ¿En cuántos años el capital invertido se triplica?
Solución: En este caso la tasa real es \(r = \frac{{7\% }}{{12}}\) y \(n\)
\(C\left( n \right) = {C_0}{\left( {1 + \frac{{0.07}}{{12}}} \right)^n}\)
Donde \({C_0}\) es el capital para invertir y \(n\) es el número, sustituyendo los datos obtenemos:
\(3{C_0} = {C_0}{\left( {1 + 0.0058} \right)^n}\)
\(3 = {\left( {1.005833} \right)^n}\)
Al aplicar logaritmo a cada miembro de la expresión anterior:
\(\log 3 = \log \left( {{{\left( {1.005833} \right)}^n}} \right)\)
\(0.47712 = n\log \left( {{{\left( {1.0058} \right)}^{}}} \right)\)
\(\frac{{0.47712}}{{0.0025259}} = n\)
\(n = 188.89\)
La respuesta es 188.89 meses se triplicará el capital, en años es equivalente a \(15.741\).
\(0.02551 = \log {C_0} + \left( {0.002526} \right)\)
Solución alternativa.
Cabe aclarar que, en esta solución, es una aproximación, y el modelo es factible porque la capitalización es mensual; en caso de que fuera semanal o diaria el resultado sería mejor.
Asumiremos que se invierte a interés continuo, es decir:
\(A\left( t \right) = {C_0}{e^{rt}}\)
Donde \({C_0}\) es el capital por invertir, \(r\) es la tasa anual y \(t\) es el tiempo en años. Al sustituir los datos se tiene la ecuación:
\(3{C_0} = {C_0}{e^{0.07t}}\)
\(3 = {e^{0.07t}}\)
Al aplicar logaritmo natural:
\(\ln 3 = \ln {e^{0.07t}}\)
\(\ln 3 = 0.07t\ln {e^{}}\)
\(\ln 3 = 0.07t\)
\(t = \frac{{\ln 3}}{{0.07}} = \frac{{1.0986}}{{0.07}} = 15.694\)
El resultado anterior es equivalente a 188.33 meses
Ejemplo práctico 2
A una persona le ofrecen una tasa de interés de tal manera que, si reinvierte su capital inicial mensualmente, al igual que los intereses generados; su capital sería duplicado en 10 años. Calcule la tasa de interés que ofrece el banco y determine en cuántos meses el capital será triplicado.
Solución: Se debe considerar que 10 años equivale a 120 meses
Para resolver el problema usaremos el modelo:
\(C\left( n \right) = {C_0}{2^{\frac{n}{{120}}}}\)
Notemos que para \(n = 120:\)
\(C\left( {120} \right) = {C_0}{2^{\frac{{120}}{{120}}}} = 2{C_0}\)
Como
\({2^{\frac{n}{{120}}}} = {\left( {{2^{\frac{1}{{120}}}}} \right)^n}\)
Se tiene
\({2^{\frac{1}{{120}}}} = 1.00579294 = 1 + 0.00579294\)
Lo anterior nos indica que la tasa mensual es de \(0.579294\% \) mensual lo cual equivale a \(12.070\% \) anual.
Para saber en cuantos meses se triplicará plantearemos la ecuación:
\(3{C_0} = {C_0}{2^{\frac{n}{{120}}}}\)
\(3 = {2^{\frac{n}{{120}}}}\)
\({\log _2}3 = \frac{n}{{120}}{\log _2}2\)
\(n = 120\left( {{{\log }_2}3} \right)\)
\(n = 120\left( {1.\;5850} \right) = 190.2\)
Nota: En caso de que tu calculadora no tenga la opción para calcular \({\log _2}3\), puedes usar:
\({\log _b}c = \frac{{{{\log }_a}c}}{{{{\log }_a}b}}\)
\({\log _2}3 = \frac{{{{\log }_{}}3}}{{{{\log }_{}}2}}\)
Ejemplo práctico en arqueología
¿Qué antigüedad tiene una figura de madera que tiene la tercera de su contenido original de carbono 14, si la vida media del material es de 5900 años?
Solución: Para resolver el problema usaremos el modelo
\(A = {A_0}{\left( {\frac{1}{2}} \right)^{\left( {\frac{t}{{5900}}} \right)}}\)
Donde: \(A\) es la cantidad de material al tiempo t y \({A_0}\) es el material inicial.
Cuando \(A = 0.14{A_0}\)
Se tiene la ecuación:
\(0.14{A_0} = {A_0}{\left( {\frac{1}{2}} \right)^{\left( {\frac{t}{{5900}}} \right)}}\)
\(0.14 = {2^{ – \frac{t}{{5900}}}}\)
\({\log _2}0.14 = – \frac{t}{{5900}}{\log _2}2\)
\({\log _2}0.14 = – \frac{t}{{5900}}\)
\( – 2.\;8365 = = – \frac{t}{{5900}}\)
\(t = \left( { – 2.\;8365} \right)\left( { – 5900} \right)\)
\(t = 16735\)
Constitución de los logaritmos
Dada la base \(b > 0,\) distinta de 1, y el número \(a > 0,\;\)podemos encontrar un número \(t\), tal que:
\(a = {b^t},\)
En tal caso se dice que \(t\), es el logaritmo de \(a\) en base \(b\), lo anterior se denota como:
\(t = {\log _b}a,\)
de inmediato se obtiene la igualdad:
\(a = {b^t} = {b^{{{\log }_b}a}},\)
Cuando la base \(b = 10\), los logaritmos se llaman logaritmos decimales y por simplicidad se usa la siguiente notación:
\({\log _{10}}a = \log a\)
Tabla de logaritmos en base 2 de las primeras potencias de dos.
| \(a\) | \({\log _b}a\) |
|---|---|
| \(1 = {2^0}\) | \({\log _2}1 = 0\) |
| \(2 = {2^1}\) | \({\log _2}2 = 1\) |
| \(4 = {2^2}\) | \({\log _2}4 = 2\) |
| \(8 = {2^3}\) | \({\log _2}8 = 3\) |
| \(16 = {2^4}\) | \({\log _2}16 = 4\) |
| \(32 = {2^5}\) | \({\log _2}32 = 5\) |
| \(64 = {2^6}\) | \({\log _2}64 = 6\) |
| \(128 = {2^7}\) | \({\log _2}128 = 7\) |
Tabla de logaritmos en base 2 de las primeras potencias de un medio.
| \(a\) | \({\log _b}a\) |
|---|---|
| \(0.5 = \frac{1}{2}\) | \({\log _2}0.5 = – 1\) |
| \(0.25 = \frac{1}{{{2^2}}}\) | \({\log _2}0.25 = – 2\)\ |
| \(0.125 = \frac{1}{{{2^3}}}\) | \({\log _2}0.125 = – 3\) |
| \(0.0625 = \frac{1}{{{2^4}}}\) | \({\log _2}0.0625 = – 4\) |
| \(0.03125 = \frac{1}{{{2^5}}}\) | \({\log _2}0.03125 = – 5\) |
| \(0.015625 = \frac{1}{{{2^6}}}\) | \({\log _2}0.015625 = – 6\) |
El sistema decimal que usamos para escribir los números favorece a los logaritmos en base diez, es por eso por lo que suelen ser los más usados para los cálculos y para la comodidad de éstos se tiene la siguiente convención:
\(\log a = {\rm{lo}}{{\rm{g}}_{10}}a\)
Tabla de logaritmos en base 10 de las primeras potencias de 10.
| \(a\) | \({\log _b}a\) |
|---|---|
| \(1 = {10^0}\) | \(\log 1 = 0\) |
| \(10 = {10^1}\) | \(\log 10 = 1\) |
| \(100 = {10^2}\) | \(\log 100 = 2\) |
| \(1000 = {10^3}\) | \(\log 1000 = 3\) |
| \(10000 = {10^4}\) | \(\log 10000 = 4\) |
| \(100000 = {10^5}\) | \(\log 100000 = 5\) |
Tabla de logaritmos en base 10 de las primeras potencias de un décimo.
| \(a\) | \({\log _b}a\) |
|---|---|
| \(0.1 = {10^{ – 1}}\) | \({\rm{log\;}}0.1 = – 1\) |
| \(0.01 = {10^{ – 2}}\) | \(\log 0.01 = – 2\) |
| \(0.001 = {10^{ – 3}}\) | \(\log 0.001 = – 3\) |
| \(0.0001 = {10^{ – 4}}\) | \(\log 0.0001 = – 4\) |
| \(0.00001 = {10^{ – 5}}\) | \(\log 0.00001 = – 5\) |
| \(0.000001 = {10^{ – 6}}\) | \(\log 0.000001 = – 6\) |
En las investigaciones de matemáticas y de otros fenómenos de física, de química, finanzas, etc., es común que aparezca el número de Euler ( \(e \approx 2.718281828 \ldots .\;\) ) elevado a una potencia y por ende es importante el cálculo de logaritmos en base \(e,\;\)los cuales son llamados logaritmos naturales (\(\ln \)) o neperianos, para simplicidad, se tiene la siguiente notación:
\(\ln a = {\log _e}a.\)
A partir de las leyes de los exponentes, se establece, las siguientes propiedades de los logaritmos en una base \(b > 0\)
\({\log _b}ac = {\log _b}a + {\log _b}c,\)\({\log _b}\frac{a}{c} = {\log _b}a – {\log _b}c,\)\({\log _b}{a^n} = n{\log _b}a.\)
No todas las calculadoras de bolsillo pueden calcular el logaritmo en cualquier base, pero sí están programadas para calcular logaritmos en base 10, las siguientes propiedades de los logaritmos permite relacionar logaritmos en diferentes bases.
\({\log _b}a{\log _a}b = 1,\)\({\log _b}c = {\log _a}c{\log _b}a.\)\({\log _b}c = \frac{{{{\log }_a}c}}{{{{\log }_a}b}}\)
De la última igualdad, al despejar\({\log _b}a.\)y sustituirlo en \({\log _b}c = {\log _a}c{\log _b}a,\) se obtiene:
\({\log _b}c = \frac{{{{\log }_a}c}}{{{{\log }_a}b}}\)
Gráfica de una función logarítmica
La función exponencial y la función logarítmica están fuertemente relacionadas. De hecho, se tienen las siguientes relaciones:
\({\log _b}{b^x} = x,\)
\({b^{{{\log }_b}x}} = x.\)
Analicemos el caso cuando \(a > 1:\)
En este caso ya sabemos que si \(p > q,\) entonces: \({a^p} > {a^q};\;\)
Sea \(0 < x < 1;\) como \({a^0} = 1,\;\) en consecuencia, \({\rm{lo}}{{\rm{g}}_a}x < 0.\) Sea \(1 < x < a;\) como \({a^1} = a,\;\) en consecuencia, \(0 < {\rm{lo}}{{\rm{g}}_a}x < 1.\) Sea \(a < x;\) como \({a^1} = a,\;\) en consecuencia, \(1 < {\log _a}x\) La gráfica de logaritmo en base \(a\), cuando \(a > 1\), se muestra a continuación
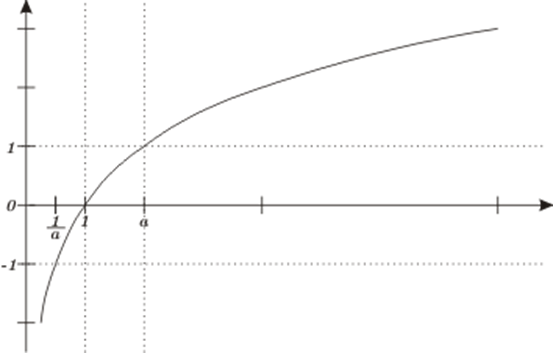
Gráfica de \({\log _a}x\) cuando \(a > 1\)
Analicemos el caso cuando \(0 < a < 1:\) En este caso ya sabemos que si \(p > q,\) entonces: \({a^p} < {a^q};\;\) Sea \(0 < x < a;\) como \({a^1} = a,\;\) entonces \({\rm{lo}}{{\rm{g}}_a}x > 1.\)
Sea \(a < x < 1;\) como \({a^1} = a < x < {a^0}\) entonces \(0 < {\rm{lo}}{{\rm{g}}_a}x < .1\)
Sea \(1 < x;\) como \({a^0} = a,\;\) entonces \({\rm{lo}}{{\rm{g}}_a}x < 0.\)
La gráfica de logaritmo en base \(a\), cuando \(a < 1\), se muestra a continuación
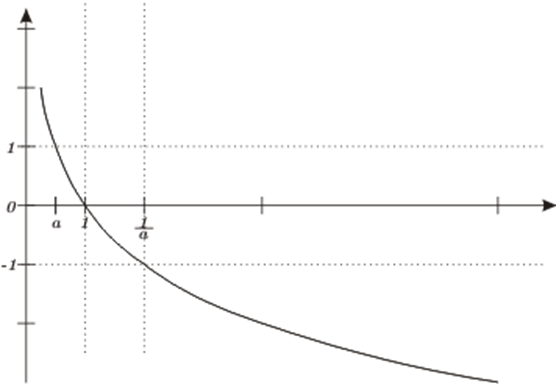
Gráfica de \({\log _a}x\) cuando \(a < 1\)
Siga en Logaritmo (parte 2)

Art. actualizado: Nov. 2022; sobre el original de septiembre, 2010.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.