Significado de impedancia Definición, cálculo, y ejemplos (resistiva, acústica y circuito rlc)

Licenciada en Física
Definición formal
La impedancia es la medida de la oposición de un sistema ante una acción periódica ejercida sobre él, que puede tomar la forma de un voltaje, una fuerza o una onda de presión, entre muchas acciones posibles.
Por ejemplo, frecuentemente, el sistema es un circuito eléctrico, cuya impedancia mide la oposición de los elementos al aplicarse un voltaje, que permite el flujo de una corriente a través de ellos.
Otros ejemplos de impedancia, son la respuesta de un medio ante una onda de presión acústica, y la oposición al movimiento que ofrece un cuerpo sometido a una fuerza. En estos casos, se trata de impedancia acústica e impedancia mecánica, respectivamente.
Cómo se calcula la impedancia
En general, la impedancia Z se calcula como la razón entre la magnitud de la acción ejercida, llamada variable de esfuerzo E y la variable de flujo del sistema F:
\(Z=\frac{Varable~de~esfuerzo}{Variable~de~flujo}=\frac{E}{F}\)
La fuerza, el voltaje, la presión, el torque y la temperatura, pueden ser variables de esfuerzo, mientras que sus contrapartes, las variables de flujo, serían la velocidad, la corriente eléctrica, el flujo de un fluido, la velocidad angular y la cantidad de calor.
En ocasiones, variables como la fuerza y la velocidad intercambian los roles, según la configuración del sistema.
En cuanto a Z, puede ser una cantidad real, pero con frecuencia, Z es una cantidad compleja o incluso vectorial.
Ejemplos dados por la impedancia resistiva, acústica y sobre un circuito RLC serie
Impedancia resistiva
Una variable de esfuerzo típica es un voltaje alterno V, aplicado entre los terminales de un circuito resistivo, siendo la correspondiente variable de flujo la corriente eléctrica I, también alterna. En un circuito como este, la impedancia equivale a la resistencia eléctrica total.
Si la impedancia es grande, se produce un flujo menor de corriente, y, por el contrario, una impedancia pequeña implica una corriente más grande. La ecuación anterior para este caso, es la familiar ley de Ohm:
V = I∙R
Donde Z es la resistencia equivalente del circuito:
\(Z={{R}_{equivalente}}\)
De manera que:
\(Z=\frac{V}{I}\)
En este caso, la unidad para la impedancia en el Sistema Internacional SI es el ohm (Ω), la misma unidad que se usa para medir la resistencia eléctrica.
Impedancia acústica
Las ondas sonoras requieren de medios materiales para propagarse, y estos ofrecen siempre alguna resistencia al paso de la onda. Esta resistencia es la impedancia acústica, declarada como el cociente dado entre la presión acústica «p» y la velocidad «v«:
\(Z=\frac{p}{v}\)
Esta expresión es análoga a la impedancia resistiva, con la presión como la variable de esfuerzo, y la velocidad como la variable de flujo.
Para la impedancia acústica Z, la unidad en SI es Pa∙s /m o N∙s/m3, pero Z también se define como el producto entre la densidad del medio ρ y la velocidad de la onda sonora en él:
Z = ρ∙v
Por lo que Z también se expresa como kg/m2∙s.
La impedancia acústica tiene importantes aplicaciones para caracterizar distintos medios, a través de las ondas sonoras.
Por ejemplo, es posible obtener una imagen del subsuelo, o del interior de una persona, si es el caso, observando el comportamiento de un pulso sonoro en cada estrato rocoso, o en cada capa de tejido, ya que cada uno tiene una impedancia diferente.
Para ilustrar la idea, la impedancia del tejido graso es diferente a la del músculo, pues la densidad, así como la velocidad del sonido, son distintas en cada uno. La impedancia del músculo resulta ser mayor a la del tejido graso.
Cuando una onda sonora incide en la interfaz entre dos medios, una parte de ella se transmite y la otra se refleja. Las componentes de la onda original, al pasar por los distintos medios, caracterizados por diferente impedancia, recogen información acerca de los mismos. Este es el fundamento de la ecografía, una técnica no invasiva para obtener imágenes médicas.
Impedancia de un circuito RLC serie
En general, un circuito eléctrico contiene diversos elementos, cuya oposición combinada al paso de corriente, representa la impedancia. Se habla de impedancia resistiva, capacitiva e inductiva, para las resistencias, capacitores e inductancias, respectivamente. Se trata de un concepto muy importante en los circuitos de corriente alterna.
Supóngase un voltaje sinusoidal de frecuencia ω constante y amplitud Vm, aplicado sobre un circuito en serie que contiene una resistencia R, un capacitor C y una inductancia L. Un circuito así se conoce como circuito RLC serie:
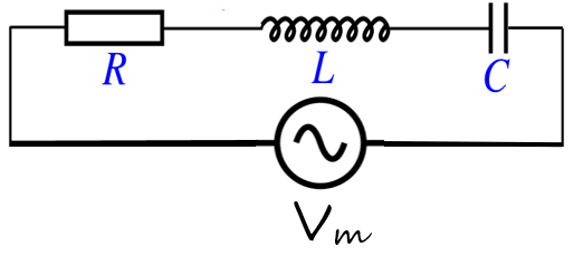
En este circuito, la impedancia Z es una cantidad compleja, es decir, tiene una parte real y una parte imaginaria. La parte real es la resistencia R del circuito, mientras que la parte compleja depende de los valores de la inductancia, la capacitancia y la frecuencia de oscilación de la fuente.
El módulo de la impedancia compleja Z, llamada simplemente “impedancia del circuito”, viene dada por la siguiente ecuación:
\(\left| Z \right|=\sqrt{~{{R}^{2}}+{{\left( \omega L-\frac{1}{\omega C} \right)}^{2}}}\)
Aquí Z también se mide en ohmios y es una cantidad muy interesante, porque permite escribir la ley de Ohm generalizada a circuitos de corriente alterna, en los casos en que el voltaje y la corriente se puedan tratar como funciones exponenciales complejas:
\({{V}_{m}}={{I}_{m}}\cdot Z\)

Trabajo publicado en: Jul., 2021.