Significado de la ley de Coulomb Definición, fórmula, fuerza eléctrica, y ejercicios

Licenciada en Física
Definición formal
La ley de Coulomb establece cuantitativamente la fuerza de atracción o repulsión que existe entre dos cargas eléctricas puntuales, consideradas tan pequeñas, que su interacción gravitatoria es despreciable.
Supone una idealización, sin embargo, las partículas cargadas que forman el átomo, como protones y electrones, se aproximan mucho a este ideal. Pero no hay que llegar tan lejos en cuanto al tamaño de las cargas: si este es muy pequeño comparado con la distancia que las separa, la fuerza entre ellas se describe acertadamente a través de la ley de Coulomb.
Esta afirma que la magnitud F de dicha fuerza es:
\(\text{F}\propto \frac{{{{\text{q}}_{\text{1}}}\text{.}{{\text{q}}_{\text{2}}}}}{{{{\text{r}}^{\text{2}}}}}\)
El símbolo “ ∝” significa “proporcional a”y en este caso se refiere a que la intensidad de la fuerza es proporcional al producto de las dos cargas que interactúan: q1 y q2, entre el cuadrado de la distancia que las separa: r2.
La forma matemática de la ley de Coulomb se parece mucho a la de la gravitación universal de Newton, pero con una diferencia importante: la fuerza entre cargas eléctricas puntuales puede ser de atracción o de repulsión, mientras que entre la fuerza de gravitación entre masas es siempre atractiva.
La constante de proporcionalidad necesaria para escribir la igualdad es la constante electrostática llamada ke o simplemente k:
\(\text{F}=\text{k}\frac{{{{\text{q}}_{\text{1}}}\text{.}{{\text{q}}_{\text{2}}}}}{{{{\text{r}}^{\text{2}}}}}\)
Y su valor depende de las unidades seleccionadas. En el Sistema Internacional de unidades este valor es 8.99 × 109 N∙m2/C2, y expresa la fuerza en newton (N), la carga en coulomb (C) y la distancia en metros (m).
El valor numérico de la constante electrostática se ha determinado experimentalmente.
Vector fuerza eléctrica
Como todas las fuerzas, la fuerza eléctrica entre cargas puntuales es un vector y está dirigido a lo largo de la línea que une las cargas. Si esta dirección se denota mediante el vector unitario \(\hat{r}\), el vector fuerza eléctrica es:
\(\vec{F}=k\frac{{{q}_{1}}.{{q}_{2}}}{{{r}^{2}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{r}\)
El principio de superposición
Cuando se tienen varias cargas eléctricas y se requiere calcular la fuerza neta que actúa sobre una sola, se aplica el principio de superposición de fuerzas, según el cual la fuerza neta es la suma vectorial de todas las fuerzas, calculadas por separado.
Por ejemplo, sea la fuerza neta que actúa sobre la carga i-ésima, debida a las cargas restantes, numeradas como j =1, 2, 3, 4…. Entonces:
\({{\text{\vec{F}}}_{\text{n}}}={{\text{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}}}_{\text{i1}}}+{{\text{\vec{F}}}_{\text{i2}}}+{{\text{\vec{F}}}_{\text{i3}}}+…=\sum{{{{\text{\vec{F}}}}_{\text{ij}}}}\)
Ejercicios de cargas
Hay tres cargas puntuales dispuestas en los vértices de un triángulo rectángulo, como se muestra en la figura. Calcular:
a) La fuerza eléctrica neta sobre la carga q2 debida a las cargas restantes.
b) E igualmente la fuerza eléctrica neta sobre la carga q3

Respuestas
a) Para calcular la fuerza neta sobre cualquiera de las cargas, es conveniente seleccionar un sistema de coordenadas cartesianas con el origen sobre la carga de interés y hacer un dibujo de las fuerzas que las restantes cargas ejercen sobre ella.
Por ejemplo, sobre la carga q2 del ejemplo actúan las fuerzas F12 y F32, ejercidas respectivamente por q1 y q3. Ahora bien, como q1 y q2 son de signos contrarios, la fuerza entre ellas es atractiva, y de igual forma, la fuerza entre q2 y q3 también es atractiva, por la misma razón.
El diagrama de cuerpo libre sobre q2 queda así:

Antes de aplicar la ley de Coulomb conviene verificar que las unidades, por ejemplo, las distancias en centímetros deben pasarse a metros y las cargas que están en micro-coulombs (μC) se deben expresar en coulombios.
Se tiene la siguiente equivalencia:
1 μC = 1 x 10-6 C
Por lo tanto, las cargas en colombios quedan así:
q1 = + 0.80 x 10-6 C; q2 = − 0.60 x 10-6 C; q3 = + 1.0 x 10-6 C
En cuanto a las distancias, 1 cm = 1 ∙ 10-2 m, entonces:
r12 = 8.0 ∙ 10-2 m= 0.08 m
Falta conocer r23, que no aparece en el dibujo provisto por el enunciado, pero que se puede encontrar a través del teorema de Pitágoras, válido para triángulos rectángulos:
\({{\text{r}}_{\text{23}}}=\sqrt{{{\left( 0.1m \right)}^{2}}-{{\left( 0.08m \right)}^{2}}}=\text{0}\text{.06 m}\)
Ahora se puede proceder a calcular las fuerzas con la ley de Coulomb:
\({{\text{\vec{F}}}_{\text{12}}}=\text{8}\text{.99}\times \text{1}{{\text{0}}^{\text{9}}}\cdot \left[ \frac{\text{0}\text{.8}\times \text{1}{{\text{0}}^{-\text{6}}}\cdot \text{0}\text{.6}\times \text{1}{{\text{0}}^{-\text{6}}}}{{{\left( 0.08m \right)}^{2}}} \right]\text{N \hat{y}}=\text{0}\text{.674 N \hat{y}}\)
\({{\text{\vec{F}}}_{\text{32}}}=\text{8}\text{.99}\times \text{1}{{\text{0}}^{\text{9}}}\cdot \left[ \frac{\text{1}.0\times \text{1}{{\text{0}}^{-\text{6}}}\cdot \text{0}\text{.6}\times \text{1}{{\text{0}}^{-\text{6}}}}{{{\left( 0.06 \right)}^{2}}} \right]\text{N \hat{x}}=\text{1}.50\text{ N \hat{x}}\)
Finalmente, aplicando el principio de superposición, la fuerza neta es:
\({{\text{\vec{F}}}_{\text{neta}}}={{\text{\vec{F}}}_{\text{32}}}+{{\text{\vec{F}}}_{\text{12}}}=\text{ 1}\text{.50 \hat{x} }+\text{ 0}\text{.674 \hat{y} N}\)
b) El procedimiento anterior es válido para calcular la fuerza resultante sobre la carga q3, solo que el diagrama de cuerpo libre difiere un poco, ya que la fuerza F13 es de repulsión y no coincide con alguno de los ejes coordenados, por lo tanto hay que descomponerla en sus componentes cartesianas, como paso previo:
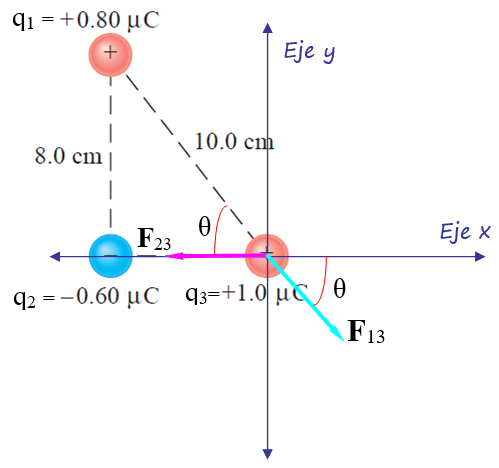
El seno y el coseno del ángulo θ son:
cos θ = 0.06 / 0.1 = 0.6
sen θ = 0.08 / 0.1 = 0.8
La fuerza F13 es:
\({{\text{\vec{F}}}_{\text{13}}}=\text{8}\text{.99}\times \text{1}{{\text{0}}^{\text{9}}}\cdot \left[ \frac{\text{0}\text{.8}\times \text{1}{{\text{0}}^{-\text{6}}}\cdot \text{1}.0\times \text{1}{{\text{0}}^{-\text{6}}}}{{{\left( 0.1m \right)}^{2}}} \right]\text{(}0.\text{6}\hat{x}-0.8\hat{y}\text{)}=\text{ }\left( \text{0}\text{.432 \hat{x}-0}\text{.575 \hat{y}} \right)N\)
Por su parte, la fuerza F23 tiene la misma magnitud y dirección que F32, pero sentido contrario. Esta última ya se calculó en el apartado anterior:
\({{\text{\vec{F}}}_{\text{32}}}=\text{1}.50\text{ N \hat{x}}\)
Por lo tanto:
\({{\text{\vec{F}}}_{\text{23}}}=-\text{1}.50\text{ N \hat{x}}\)
Por último, se aplica la superposición para encontrar la fuerza resultante sobre la carga q3:
\({{\text{\vec{F}}}_{\text{neta}}}={{\text{\vec{F}}}_{\text{13}}}+{{\text{\vec{F}}}_{\text{23}}}=\left[ \text{ }\left( \text{0}\text{.432 \hat{x}-0}\text{.575 \hat{y}} \right)\text{-1}\text{.50 \hat{x}} \right]\text{ N}=\left[ \text{-1}\text{.068 \hat{x} -0}\text{.575 \hat{y}} \right]\text{ N}\)

Trabajo publicado en: Ene., 2021.