Significado de ley de Ohm Definición, resistencias en serie y paralelo, circuitos Óhmicos y no-Óhmicos, y ejercicios

Licenciada en Física
Definición formal
La ley de Ohm establece la relación que hay entre tres importantes magnitudes de los circuitos eléctricos: voltaje, representado por la sigla V, intensidad de corriente, expresado por la sigla I, y resistencia eléctrica, declarado por la sigla R, configurando la ecuación que las relaciona, en un circuito de corriente directa, como V = I∙R.
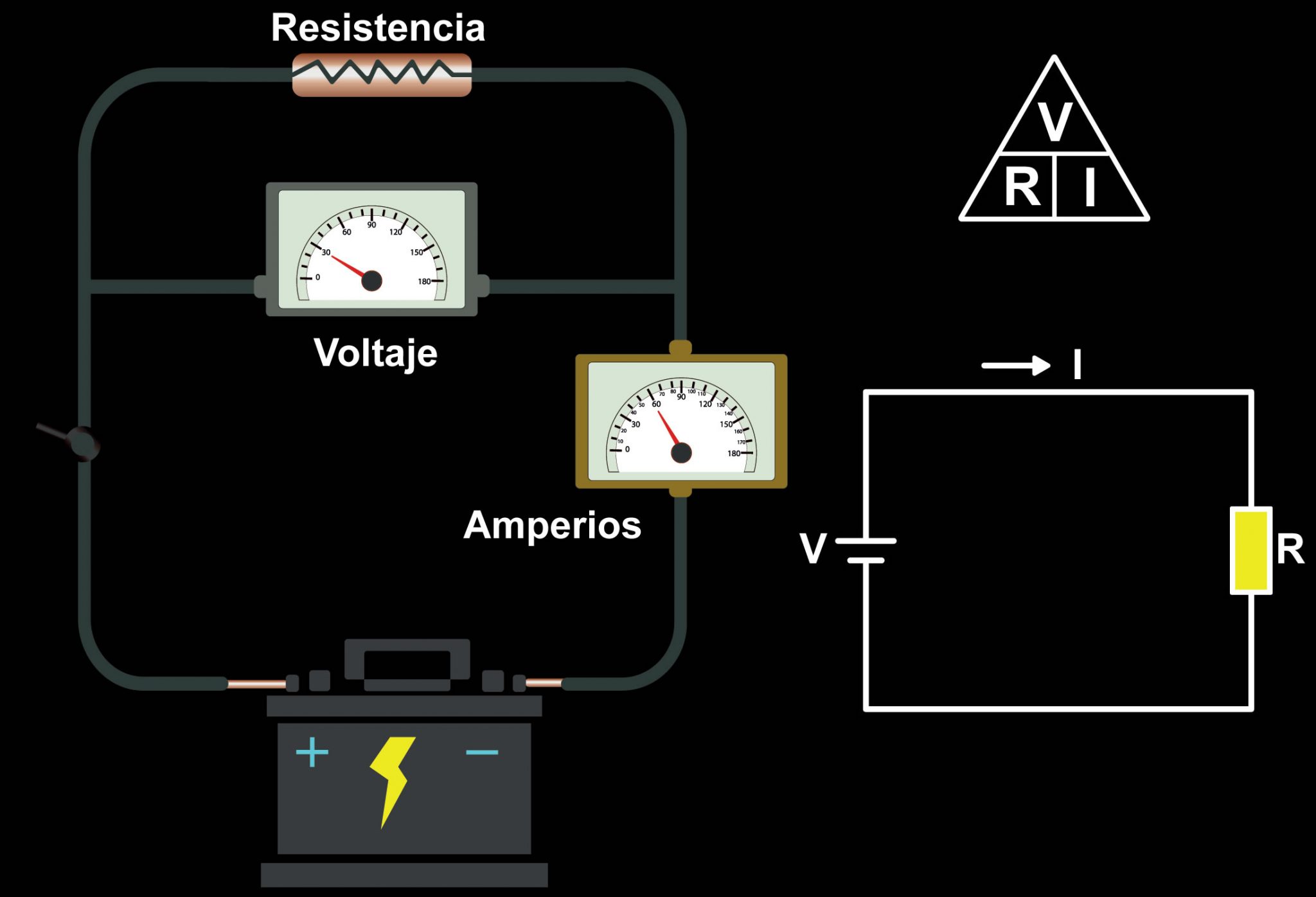
El voltaje (en voltios, V) se vincula al trabajo que hay que hacer para mover las cargas eléctricas, la corriente eléctrica (en amperios, A) es el paso de las mismas a través del material y la resistencia (en ohmios, Ω) se define como la oposición que presenta el elemento del circuito a la corriente.
La ley de Ohm pauta que entre voltaje y corriente, al menos para una gran cantidad de materiales, existe una relación lineal. Esto significa que el voltaje es directamente proporcional a la corriente, de modo tal que si aquel aumenta, esta lo hará también.
Por lo tanto, al graficar el voltaje en función de la corriente, se obtiene una línea recta que pasa por el origen, cuya pendiente es la resistencia del elemento atravesado por la corriente.
Si se grafica la corriente en función de la resistencia, igualmente se obtiene una línea recta que también pasa por el origen, con la diferencia de que en este caso la pendiente es el inverso de la resistencia 1/R, una magnitud conocida como conductancia.
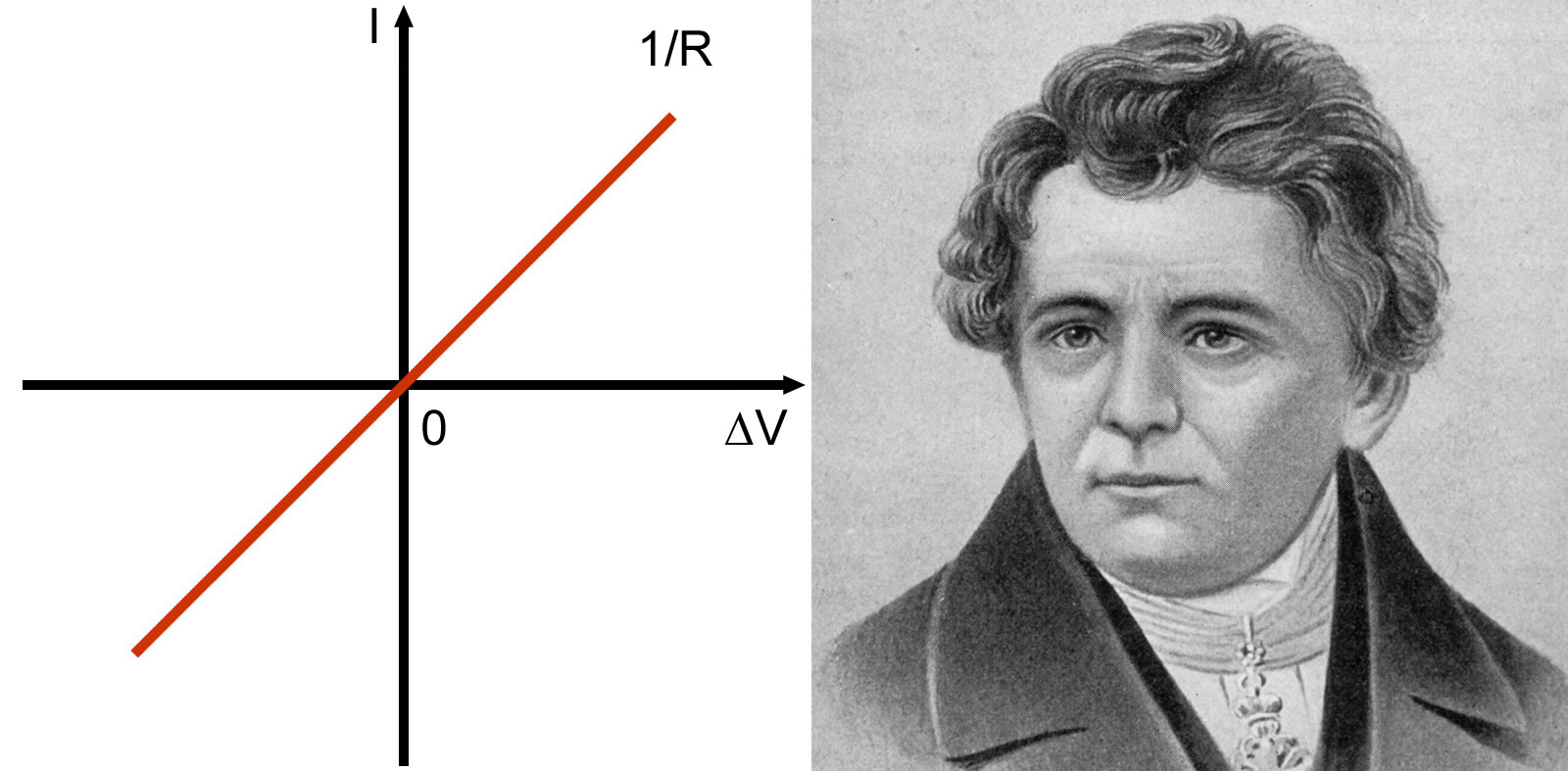
La ley de Ohm debe su nombre al físico alemán Georg S. Ohm (1789-1854), quien la determinó en forma experimental y la dio a conocer por primera vez en un artículo publicado en 1827.
Materiales y circuitos óhmicos y no-óhmicos
No todos los materiales ni elementos de circuito cumplen con la ley de Ohm, a aquellos que sí lo hacen se denominan óhmicos. Las resistencias eléctricas comerciales son un buen ejemplo de elementos que sí cumplen la ley de Ohm, pero los diodos no, ni tampoco todos los materiales conductores.
Para distinguir experimentalmente los elementos óhmicos de los no óhmicos hay que examinar su gráfica corriente versus voltaje, de modo que si esta es una línea recta, el elemento sigue la ley de Ohm y su resistencia es constante; en cambio, si se obtiene otra curva, el elemento es no-óhmico.
La ley de Ohm no es una ley física en sentido estricto, ya que es válida únicamente para ciertos materiales, sin embargo se cumple para una gran cantidad de ellos, cuya resistencia se mantiene constante. Esto es importante al momento de anticipar cuánta corriente pasa por determinado elemento en circuito óhmico y saber cómo se va a comportar. Así por ejemplo, la ley de Ohm se cumple en numerosos artefactos de uso común, como por ejemplo, las resistencias en las cocinas eléctricas o los calentadores de agua.
Resistencias en serie y en paralelo
Antes de aplicar la ley de Ohm a un caso concreto, se examinan dos formas simples de conectar resistencias, que aparecen frecuentemente en los circuitos eléctricos. Estas formas son:
– Conexiones en serie
– Conexiones en paralelo.
Cuando las resistencias se conectan en serie, la misma corriente pasa por todas, en cambio, cuando se conectan en paralelo, la corriente de entrada se divide según la ley de Ohm: por una resistencia grande pasará menos corriente que por una resistencia pequeña.

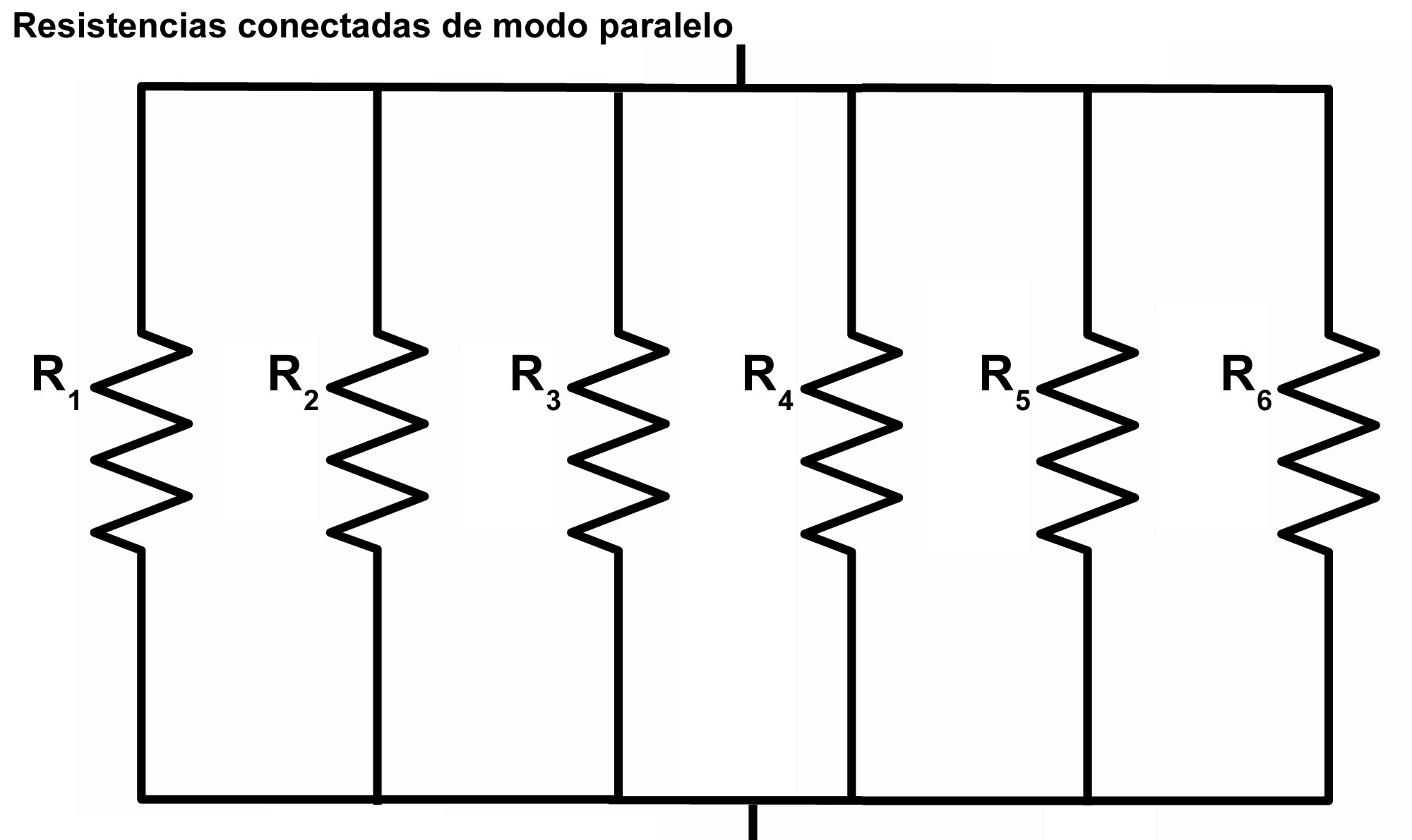
Las resistencias en serie pueden sustituirse por una sola resistencia que representa el mismo papel dentro del circuito, llamada resistencia equivalente. Lo mismo ocurre con dos o más resistencias en paralelo, que igualmente pueden ser sustituidas por su resistencia equivalente.
Para encontrar la resistencia equivalente de un conjunto de resistencias en serie se aplica la ecuación:
\(R_{eq} = R_{1} + R_{2} + R_{3}+… = \sum\limits_{i=1}^{n}{{{R}_{i}}}\)
Y para las resistencias en paralelo se tiene:
\(\frac{1}{{{R}_{eq}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}+…=\sum\limits_{i=1}^{n}{\frac{1}{{{R}_{i}}}}\)
Ejercicios: La ley de Ohm en la resolución de circuitos
En el circuito mostrado en la siguiente figura determinar:
A) La resistencia equivalente.
B) El valor de la corriente que pasa por la batería.
C) La corriente que pasa por la resistencia de 12 ohmios.
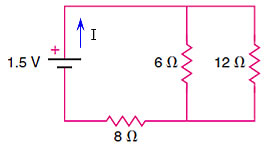
Nota: la corriente se supone siempre que sale del terminal + y entra al terminal – de l batería.
Respuesta A
Las resistencias de 6 Ω y 12 Ω están en paralelo, ya que la corriente I suministrada por la batería se divide cuando llega a ellas. Al aplicar la fórmula para resistencias en paralelo, se obtiene una resistencia equivalente que las sustituye:
\(\frac{1}{{{R}_{eq}}}=\frac{1}{6\Omega }+\frac{1}{12\Omega }=\frac{1}{4\Omega }\)
Por lo tanto:
\(R_{eq} = 4 \Omega\)
Esta resistencia quedaría a su vez en serie con la resistencia de 8 Ω, por lo tanto la resistencia equivalente definitiva es:
\(R_{eq} = 4 \Omega + 8 \Omega = 12 \Omega\)
El circuito mostrado se puede sustituir por uno que tenga la batería de 1.5 V en serie con una resistencia de 12 Ω.
Respuesta B
Aplicando la ley de Ohm al circuito reducido en a), la corriente es:
\(I=\frac{V}{R}=\frac{1.5V}{12 \Omega }=0.125A\)
Respuesta C
La corriente que sale de la batería se divide al llegar al paralelo:
\(I = I_{6 \Omega} + I_{12 \Omega} = 0.125 A\)
Pero antes hay que notar que como ambas están en paralelo, se encuentran al mismo voltaje, pero este no es el mismo que el de la batería, pues esta tensión se divide entre el paralelo y la resistencia de 8Ω así:
\(V = V_{8\Omega} + V_{paralelo} = (IR)_{8\Omega} + V_{paralelo}\)
Por lo tanto:
\(V_{paralelo} = 1.5 V – (0.125 A x 8 Ω) = 0.5 V\)
Las resistencias del paralelo están a 0.5 V. Sabiendo el voltaje, la corriente en la resistencia de 6 Ω se calcula directamente:
\(I=\frac{V}{R}=\frac{0.5V}{6\Omega }=0.0833A\)

Trabajo publicado en: Oct., 2020.
Ilustraciones: Umaruchan, Fridas, Archivist, Narayana, Luisrftc