Significado de magnitudes escalares y vectoriales Definición, y características

Licenciada en Física
Definición formal
Las magnitudes escalares y vectoriales se distinguen porque las primeras solo tienen valor numérico, mientras que las segundas tienen, además de valor numérico, dirección y sentido. Esto da como resultado que los vectores reciban un tratamiento matemático muy distinto al de los escalares, pues es necesario tomar en cuenta estos tres atributos a la vez.
La Física asocia escalares o vectores a determinadas magnitudes, según su naturaleza. Como ejemplos, se pueden citar el tiempo, la temperatura, el volumen y la capacidad de un recipiente.
Para especificar del todo una temperatura, basta con el valor numérico y la unidad apropiada. Lo mismo se puede afirmar de un intervalo de tiempo o el caudal de un río.
Sin embargo, el efecto de una fuerza depende de la dirección y el sentido en que se aplique. Por ejemplo, el resultado de ejercer una fuerza vertical sobre un objeto, es muy diferente al que se obtiene a través de una fuerza de igual magnitud, actuando en dirección horizontal.
Simplemente, no es posible alzar un objeto sobre el suelo empujándolo hacia un lado. La dirección y el sentido cuentan mucho a la hora de obtener un resultado en particular.
Características de las magnitudes escalares
Para especificar una magnitud escalar hace falta un valor numérico y una unidad apropiada. El tiempo es un escalar usado con mucha frecuencia, su valor siempre es positivo y hay muchas unidades para medirlo, dependiendo de la duración del suceso.
El Sistema Internacional de Unidades SI es el estándar en ciencia e ingeniería. En este sistema, el tiempo se mide en segundos, pero por supuesto se manejan otras unidades, como minutos, segundos, horas, días, años y muchas más. Y si el evento es muy breve, se usan los submúltiplos del segundo, como el milisegundo, el microsegundo y otros.
La distancia es otro escalar muy familiar, que también es positivo y se mide en unidades de longitud. No debe confundirse con el desplazamiento, que es un vector cuyas características se estudiarán en breve.
Para las distancias, la unidad SI es el metro, pero, al igual que sucede con el tiempo, hay muchos patrones para medirla: centímetros, kilómetros, pies, pulgadas, millas y más.
Los escalares se pueden sumar o restar según convenga, y también son posibles otras operaciones combinadas entre diferentes magnitudes. En todo caso, la suma o resta debe hacerse exclusivamente entre magnitudes de similar naturaleza.
Esto quiere decir que los tiempos solo se pueden sumar o restar con otros tiempos, las distancias con otras distancias, y así sucesivamente.
Pero se puede dividir una distancia entre un tiempo para obtener una rapidez o celeridad, que también es un escalar y no se debe confundir con la velocidad.
Otros escalares significativos en la vida diaria son la masa, la temperatura, la densidad, la energía (de todo tipo, incluida la de los alimentos), la capacidad de un recipiente, la resistencia eléctrica y el voltaje, por mencionar solo algunos.
Características de las magnitudes vectoriales
Poseen cualidades direccionales o geométricas, por lo que, aparte de un valor numérico y una unidad, hay que especificar dirección y sentido. Esta información direccional es tan relevante como el valor numérico.
Supóngase que el perrito de la imagen se mueve una distancia de 4 metros partiendo del origen. Con esta información, la posición final del perrito podría ser cualquier punto de una circunferencia de radio 4m, centrada en el punto de partida.
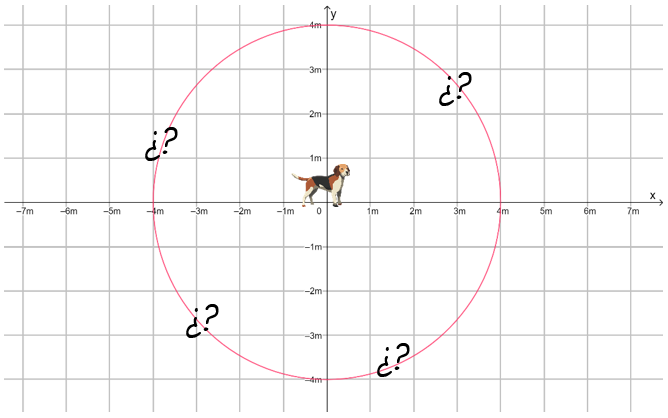
La distancia recorrida, que es un escalar, no ofrece información suficiente acerca del movimiento. Ahora bien, sabiendo que el perrito se movió 4m horizontalmente, su posición final sigue siendo ambigua, ya que pudo haber viajado a la izquierda o a la derecha.
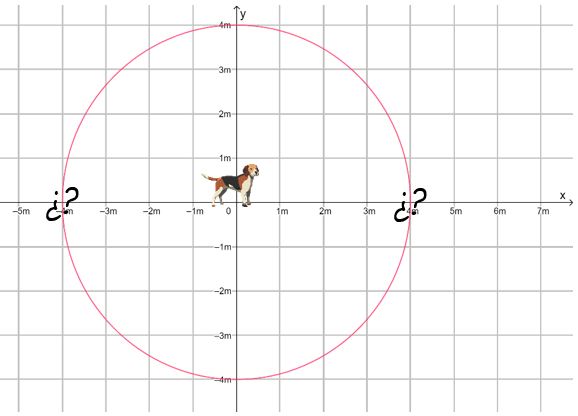
Solo cuando se especifica que el perrito se movió 4 m en dirección horizontal hacia la derecha, es que se tiene la información completa sobre su desplazamiento.
Por lo tanto, el desplazamiento es una magnitud vectorial, y en este ejemplo sus tres características son:
• Magnitud o módulo: 4m
• Dirección: horizontal
• Sentido: hacia la derecha
Todos estos atributos se indican mediante la flecha de color azul, que va desde el punto de partida hasta el de llegada. Por eso los vectores se representan geométricamente mediante flechas. Cuya longitud iguala la del módulo del vector.
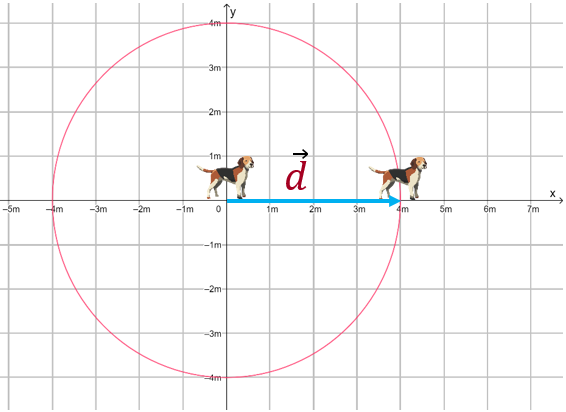
El vector desplazamiento del perrito se denota con una letra mayúscula o minúscula, y una flechita por encima. Si esta opción no está disponible en texto impreso, también se puede emplear la letra negrita. De esta manera:
\(\vec{d}=d\)
En todo caso, es necesario distinguir siempre el vector de su magnitud, que en este caso es la distancia recorrida. Esta última se puede escribir con una letra normal, simplemente “d”, o bien añadiendo al vector las barras de valor absoluto: \(~~\left| {\vec{d}} \right|\), para enfatizar que se trata del módulo del vector.
Aparte del vector desplazamiento, otros vectores importantes son la velocidad, la aceleración, la fuerza, el momentum, el momento angular, el campo eléctrico y el campo magnético.
Con los vectores se pueden llevar a cabo sumas y restas, siempre que se trate de vectores que representen la misma magnitud física. La suma vectorial se realiza siguiendo unas reglas particulares que toman en cuenta la dirección y el sentido de los sumandos. El resultado también es un vector.
Asimismo, entre vectores se definen dos clases de productos, y también es posible multiplicar un escalar por un vector. Tales productos describen matemáticamente diferentes magnitudes físicas, como la fuerza, el torque, el campo magnético, el flujo del campo eléctrico y muchas más.

Trabajo publicado en: Jul., 2021.