Definición de Paralaje Estelar

Ángel Zamora Ramírez
Licenciado en Física

Se le llama Paralaje Estelar al cambio de posición aparente que sufren las estrellas cercanas cuando son observadas desde dos puntos opuestos de la órbita terrestre. Este fenómeno sirve para saber qué tan lejos están las estrellas cercanas de nosotros debido a que midiendo el cambio aparente de posición de estas se puede calcular la distancia a la que se encuentran.

Principios y ejemplos del paralaje estelar

Te propongo el siguiente experimento: Estira por completo uno de tus brazos de tal manera que tu mano quede justo frente a tus ojos, después levanta tu dedo índice. Una vez hecho esto mira directamente tu dedo y tapa uno de tus ojos, ahora destapa tu ojo y tapa el otro. Al hacer esto podrás percatarte que tu dedo parece cambiar de posición. Esto es así debido a que estamos mirando nuestro dedo desde dos puntos de referencia separados entre sí (nuestros ojos) frente a un fondo estático. Esta simple observación es la idea principal detrás del paralaje estelar.

En el ejemplo vimos nuestro dedo con cada uno de nuestros ojos y hemos observado cómo parece cambiar de posición, pero, ¿cómo podríamos hacer algo así con las estrellas que se aprecian en la noche? Bueno, pues nuestra mejor aliada en esto será la órbita terrestre.

Para poder observar este mismo fenómeno con las estrellas basta con tomar una imagen del cielo nocturno un día y volver a sacar una imagen del mismo punto del cielo 6 meses después. De este modo tendremos dos imágenes de las mismas estrellas vistas desde dos puntos opuestos de la órbita terrestre, de la misma manera en que observamos nuestro dedo desde dos ojos distintos. Al sobreponer ambas imágenes podremos ver cómo algunas estrellas parecen encontrarse en posiciones distintas.

Ahora bien, ¿cómo es que esto nos puede ser útil para calcular la distancia a la que se encuentran dichas estrellas? Resulta que el cambio de posición aparente que sufren las estrellas es inversamente proporcional a la distancia a la cual se encuentran, es decir, entre más lejanas estén menor es su cambio de posición. Para ver esto consideremos la imagen inferior.

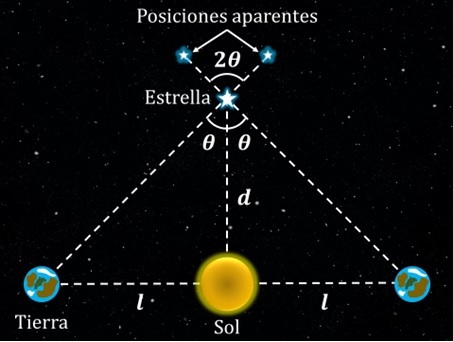
Aquí tenemos a la Tierra en dos posiciones opuestas de su órbita alrededor del Sol, vamos a olvidarnos por este momento de la excentricidad de la órbita y consideramos que en ambas posiciones la Tierra se encuentra a una distancia l del Sol cuyo valor es de l=1 AU. Esta unidad se llama “Unidad Astronómica” y es la distancia promedio entre la Tierra y el Sol, el valor de esta unidad es de aproximadamente \(1 AU≈1.49×10^11 m\).

Consideremos a una estrella cualquiera vista desde estos dos puntos de referencia, donde d es la distancia entre dicha estrella y el Sol. Podemos apreciar las posiciones aparentes de la estrella vista desde puntos opuestos de la órbita terrestre, por definición vamos a decir que la distancia angular entre estas dos posiciones aparentes es de 2θ.

Lo que se forma en este esquema es un triángulo rectángulo cuyos catetos son las distancias l y d, y cuyo ángulo superior es θ. Por lo tanto, podemos calcular la distancia d simplemente utilizando las razones trigonométricas de toda la vida. Tenemos que:

\(tan⁡θ=\frac{1}{d}\)

Los ángulos de paralaje en realidad son muy pequeños, tan sólo para darnos una idea, Próxima Centauri es la estrella más cercana a nuestro Sistema Solar y se encuentra a una distancia de aproximadamente 4.22 años luz (ly). Esta estrella sufre un paralaje de apenas unos 0.77” (segundos de arco), lo cuál equivale a 0.0002°. En este límite podemos hacer una aproximación que nos facilita el cálculo, cuando θ es muy pequeño \(tan⁡θ≈θ\), por lo tanto, en la ecuación anterior podemos decir que:

\(θ= \frac{1}{d}\)

Resolviendo para d obtenemos:

\(d= \frac{1}{θ}\)

De esta manera, se puede calcular la distancia a la que se encuentra una estrella con su paralaje. Como podemos observar, entre menor sea el ángulo de paralaje mayor es la distancia a la que se encuentra dicha estrella. No obstante, vamos a modificar un poco esta expresión para obtener una que sea más útil en el contexto astronómico. Primero vamos a sustituir el valor de l de tal manera que:

\(d= \frac{1}{θ} AU\)

En este caso el ángulo θ está medido en radianes, no obstante, como hemos visto anteriormente es más conveniente utilizar segundos de arco (“) en estas mediciones. Considerando que \(1 rad≈206265”\) tenemos que:

\(d= \frac{206265}{θ”} AU\)

Donde θ” indica que el ángulo está medido en segundos de arco. Vamos a definir una nueva unidad para medir distancia llamada “pársec (pc)” que equivale a \(1 pc=206265 AU\). Esto nos permite finalmente expresar la ecuación anterior como:

\(d= \frac{1}{θ”} pc\)

Donde la distancia obtenida tendrá unidades de pársecs (pc). Por definición 1 pc es la distancia a la cual un objeto astronómico presentará un paralaje de 1” y equivale a \(1 pc≈3.26 ly≈3.09×10^13 km\).

Cómo mencionamos anteriormente, la estrella más cercana a nosotros presenta un paralaje de 0.77”, por consiguiente, las estrellas que se encuentren más lejos presentarán paralajes cada vez más pequeños hasta que sean imperceptibles. Es por ello que el método de Paralaje Estelar sirve solamente para calcular la distancia de estrellas que se encuentren cercanas a nosotros.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Ene., 2024.

Datos para citar en modelo APA: Zamora Ramírez, A. (enero, 2024). Definición de Paralaje Estelar. Significado.com. Desde https://significado.com/paralaje-estelar/