Significado de plano cartesiano Definición, ejemplos, puntos y regiones

Licenciada en Física
1. Marco de espacio bidimensional formado por dos rectas numéricas infinitas (el eje X, de modo horizontal, y el eje Y, de modo vertical) que se encuentran perpendicularmente en el origen (0,0). La ubicación de un punto (X,Y) dentro del plano se denomina coordenada numérica y se expresa como un par ordenado entre distancia y altura.
Etimología: En homenaje al filósofo-matemático francés Descartes (1596-1650), adaptado su nombre en la forma del latín Cartesianus, respecto de Cartesius, manifestando el planus cartesianus.
Cat. gramatical: Sustantivo masc.
En sílabas: pla-no + car-te-sia-no.
Plano Cartesiano
Definición formal
El plano cartesiano es una construcción geométrica que permite trabajar curvas y figuras sobre dos rectas posicionadas de modo perpendicular entre sí; una horizontal (denominado eje x o eje de las abscisas) y otra vertical (eje y o eje de las ordenadas). De esta manera, el plano queda dividido en cuatro regiones segmentadas como cuadrantes, los cuales se denotan con números romanos y se cuentan en sentido antihorario.
Los ejes x e y, llamados ejes cartesianos, se cortan en un punto O llamado el origen del sistema de coordenadas. Sobre los ejes coordenados se toma una escala que servirá para ubicar un punto P especificando sus coordenadas x e y, siempre en ese orden: primero la coordenada x y luego la y. Este par de coordenadas es único para cada punto y de esta manera P queda totalmente especificado. En dicha escala, los valores ubicados del 0 hacia la derecha y del 0 hacia arriba son positivos, y negativos si se localizan a la izquierda y hacia abajo del 0.

El nombre responde al matemático y filósofo francés René Descartes (1596-1650), aunque la idea en sí no fue invento suyo, ya que había comenzado a gestarse tiempo atrás, gracias al trabajo de numerosos pensadores y científicos. El gran matemático y contemporáneo de Descartes, Pierre de Fermat (1601-1665) llegó por su cuenta también a desarrollar los mismos principios que combinaban la geometría con el álgebra en una nueva disciplina: geometría analítica.
Trazado de puntos en el plano cartesiano
Para encontrar un punto P cuyas coordenadas (x,y) se conocen, se sigue el siguiente procedimiento:
-Se comienza por la coordenada x o por la y, es indiferente. Comenzando por la coordenada x, se desplaza la punta del lápiz sobre el eje horizontal hacia la derecha, si la coordenada es positiva, o hacia la izquierda si es negativa.
-Una vez localizada la coordenada x, se debe mover el lápiz verticalmente hacia arriba si la coordenada y es positiva o hacia abajo si es negativa. Si la coordenada y es 0, ya queda localizado el punto de una vez.
-Como último paso, dibujar el punto.
Ejemplos de puntos en el plano cartesiano
Graficar los siguientes puntos en el plano cartesiano:
.P1(3,4)
.P1(-2,7)
.P3(-4,-6)
.P4(3,-5)
El plano cartesiano se puede dibujar a mano sobre un papel cuadriculado, con ayuda de una regla milimetrada. La escala se mide con la regla o dividiendo los ejes mediante la cuadrícula ya impresa. Existen programas en línea gratuitos para graficar puntos y otras curvas y figuras en el plano cartesiano, por ejemplo Geogebra es una calculadora gráfica en línea muy conocida y con muchas funciones. Con esta calculadora online los puntos indicados son:
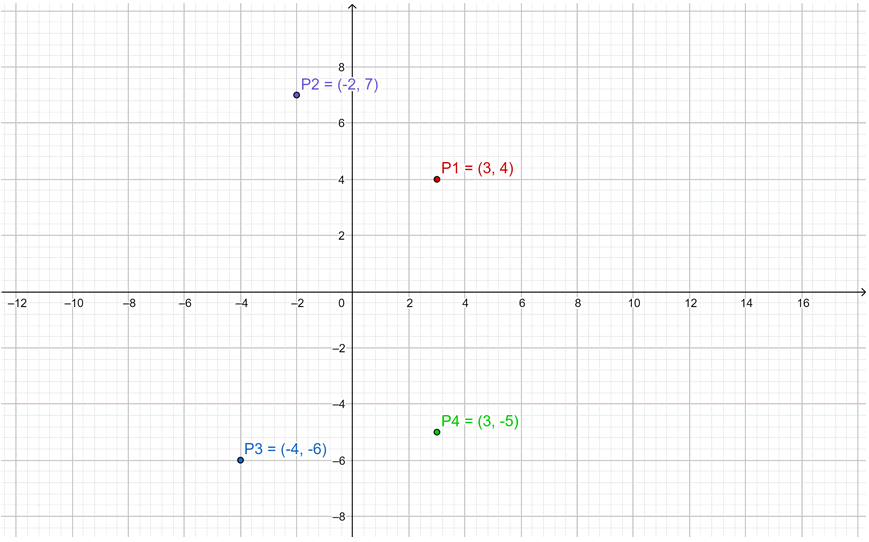
Obsérvese que el punto P1 está en el primer cuadrante (ambas coordenadas positivas), el punto P2 pertenece al segundo cuadrante (coordenada x negativa, coordenada y positiva), el P3 está en el tercer cuadrante (las dos coordenadas son negativas) y P4 se ubica en el cuarto cuadrante 8coordenada x positiva, coordenada y negativa).
Regiones en el plano cartesiano
En el plano cartesiano no solamente se pueden ubicar puntos, sino también regiones o conjuntos de puntos, por ejemplo están las regiones:
a) x + y < 3
b) x2 − 9 > 0
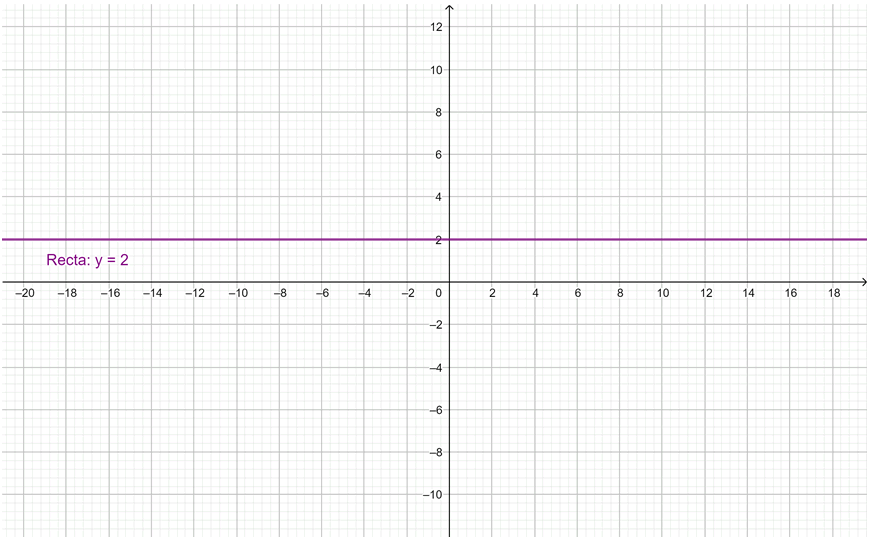
c) y =2
Sus respectivas gráficas aparecen a continuación, la región de interés coloreada;
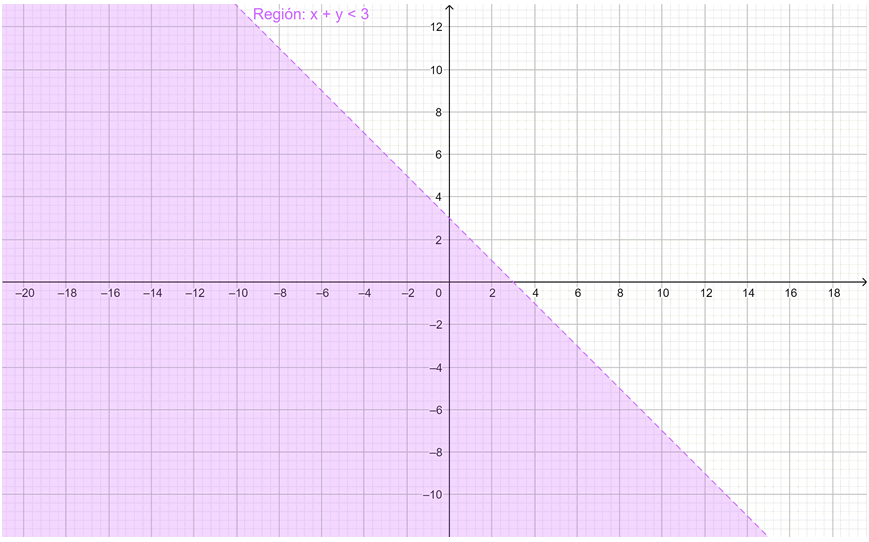
a) La región x + y < 3 corresponde a los puntos tales que y < -x + 3, es decir, son los puntos por debajo de la recta y = -x + 3 que sirve de límite a la región.
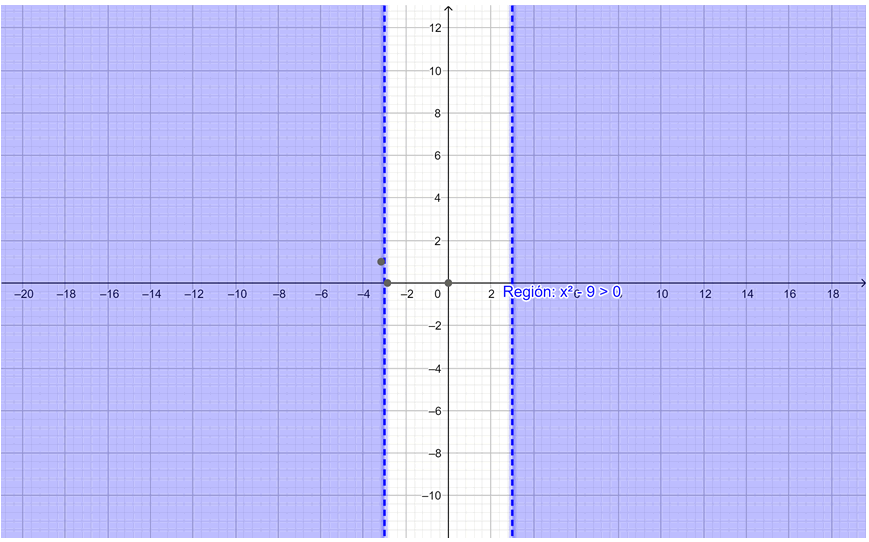
b) La región x2 – 9 > 0 corresponde a los puntos que cumplen:
x2 > 9
Lo cual significa que:
c) Finalmente, los puntos que cumplen la condición y = 2 caen sobre la recta horizontal que pasa por y =2.
Ejemplo de aplicación
Los vértices de un rectángulo se encuentran en los puntos:
.A(8,10)
.B(-10,10)
.C(-10,-4)
.D(8,-4)
¿Cuál es el perímetro del rectángulo y cuál es su área?
Respuesta
El primer paso es marcar los puntos en el plano cartesiano y luego unirlos para formar el rectángulo. El perímetro se calcula sumando las longitudes de todos sus lados, en la gráfica, el lado que une los puntos A y B mide 18 unidades, lo cual se calcula fácilmente contando los cuadrados: hay 9 cuadrados de diferencia, pero nótese que cada uno vale 2 unidades según la escala.
La distancia también se puede encontrar fácilmente calculando el valor absoluto de la diferencia entre las coordenadas horizontales de cada punto. El valor absoluto es necesario, pues la distancia siempre es una cantidad positiva:
\({{d}_{AB}}=\left| {{x}_{B}}-{{x}_{A}} \right|=\left| -10-8 \right|=\left| -18 \right|=18\)
De forma análoga se encuentra la distancia entre los puntos B y C, pero como esta distancia es vertical, se halla el valor absoluto de la resta de las coordenadas:
\({{d}_{BC}}=\left| {{y}_{C}}-{{y}_{B}} \right|=\left| -4-10 \right|=\left| -14 \right|=14\)
El perímetro P del rectángulo es:
P = 2dAB + 2dBC = (2 ∙ 18) + (2 ∙ 14) = 64 unidades
El área A del rectángulo es el producto de su base por la altura:
A = 18 ∙ 14 unidades de área = 252 unidades de área.


Trabajo publicado en: Ene., 2021.