Significado de poliedros (regulares e irregulares, convexos y cóncavos) Definición, teorema de Euler

Licenciada en Física
Definición formal
Los poliedros son modelos geométricos cuya construcción tridimensional está formada por caras que remiten a un polígono. No necesariamente se trata de objetos sólidos o macizos, lo que implica que, por ejemplo, una caja de base rectangular es también un poliedro, al que se le conoce como paralelepípedo, pero hay muchos más, como pirámides, prismas y poliedros estrellados. En cambio, cilindros y conos no son poliedros.
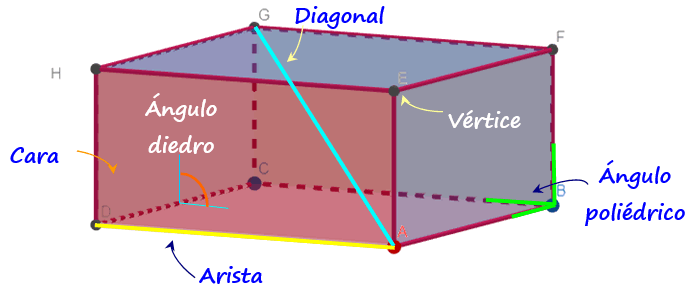
Elementos constitutivos
Básicamente un poliedro está conformado por los siguientes elementos, que a modo de ejemplo se muestran en el paralelepípedo de la imagen arriba, uno de los poliedros más sencillos y conocidos:
– Caras, de forma poligonal, que en el paralelepípedo son 6 rectángulos.
– Aristas, lados que se forman por la unión de dos caras. Hay 12 en la figura.
– Vértices o esquinas, en los que se conectan las aristas, denotados con letras mayúsculas A, B, C… en la imagen. El paralelepípedo tiene 8 vértices.
– Ángulo diedro, es el que se forma entre caras contiguas del poliedro, que son las que tienen una arista en común. El paralelepípedo tiene 12 ángulos diedros.
– Ángulo poliédrico, formado por las caras que concurren en un mismo vértice, por lo que el paralelepípedo tiene 8 ángulos poliédricos, que en este caso son triedros ya que se forman por la concurrencia de tres caras, pero eso depende de la figura.
– Diagonales, segmentos que unen vértices enfrentados.
Tipos de poliedros a base de tres criterios
I) Por el número de caras

De acuerdo al número de sus caras, hay poliedros de 4, 5, 6 y más caras. Algunos tienen nombres especiales derivados del griego:
– Tetraedro (4 caras)
– Pentaedro (5 caras)
– Hexaedro (6 caras)
– Heptaedro (7 caras)
– Octaedro (8 caras)
– Icosaedro (20 caras)
II) Por la medida del ángulo diedro: convexos y cóncavos
El ángulo diedro es el ángulo que se forma entre dos caras del poliedro, las cuales se intersectan. Para encontrarlo hay que ubicarse sobre la arista común a las dos caras, luego trazar segmentos perpendiculares a la arista sobre cada cara, partiendo de un punto común sobre ella, tal como se observa en la figura del comienzo. La medida del ángulo entre estos segmentos corresponde a la del ángulo diedro, que en el caso del paralelepípedo o el cubo mide 90º.
Poliedros convexos
Son aquellos cuyos ángulos diedros miden menos de 180º. En tal caso, el segmento que une a dos puntos cualesquiera del interior del poliedro, queda siempre dentro de la figura.
Los poliedros mostrados en las figuras anteriores son convexos.
Poliedros cóncavos
Son los poliedros que tienen al menos un ángulo diedro mayor de 180º, lo cual quiere decir que presentan salientes. Los poliedros estrellados son ejemplos de poliedros cóncavos.
III) Por la congruencia de sus caras y de sus ángulos diedros: regulares e irregulares
El tercer criterio para clasificar los poliedros contempla la congruencia (igualdad de medidas) de sus caras y ángulos diedros. De acuerdo a ello se tienen poliedros regulares o poliedros irregulares.
Poliedros regulares
Son aquellos cuyas caras son polígonos regulares y congruentes entre sí, y además sus ángulos diedros tienen la misma medida. Existen únicamente cinco poliedros regulares:
– Tetraedro, poliedro de 4 caras con forma de triángulo equilátero
– Hexaedro regular o cubo, que posee 6 caras cuadradas
– Octaedro, lo conforman 8 triángulos equiláteros
– Dodecaedro, constituido por 12 pentágonos (polígono de 5 lados)
– Icosaedro, su superficie consta de 20 triángulos equiláteros.
A estos poliedros se les llama sólidos pitagóricos, ya que los antiguos matemáticos griegos los habían identificado y asociado a los cuatro elementos que consideraban relevantes para la vida: fuego (tetraedro), tierra (cubo), aire (octaedro) y agua (icosaedro). Más tarde Platón asoció el dodecaedro con el universo, por ello también se habla de sólidos platónicos.
Poliedros irregulares
Son los poliedros cuyas caras no son congruentes o no lo son sus ángulos diedros. Por ejemplo:
– Prismas (como el de la figura)
– Pirámides de base cuadrada
– Pentaedros y heptaedros
Teorema de Euler para los poliedros
El teorema relativo a los poliedros convexos y enunciado por el gran matemático suizo Leonhard Euler (1707-1783) establece una curiosa relación entre el número de caras (C), el de las aristas (A) y el de los vértices (V), de la siguiente manera:
C + V − A = 2
Por ejemplo, en el caso del paralelepípedo, se sabe que tiene 6 caras y 8 vértices, por lo tanto, C = 6 y V = 8, de allí que el número de aristas sea:
A = C + V − 2 = 6 + 8 − 2 = 12
Puede verificarse que el teorema se cumple para cualquier poliedro convexo, por ejemplo, imaginando que se hace un corte rasante en una esquina del paralelepípedo, queda una esquina truncada, dando lugar a un poliedro que tiene 7 caras y 10 vértices, en cuyo caso el número de aristas es, de acuerdo al teorema de Euler para poliedros:
A = C + V − 2 = 7 + 10 − 2 = 15

Trabajo publicado en: Mar., 2021.