Definición de Polinomios

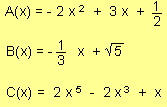A Instancias de las matemáticas se designa con el término de polinomio a la suma de varios monomios (expresiones algebraicas), porque un polinomio es una expresión algebraica, constituida por una o más variables, utilizando únicamente las operaciones aritméticas de suma, resta, multiplicación y exponentes numéricos positivos. El polinomio que presenta un único término se denomina monomio, el de dos, binomios y el de tres, trinomios.

Si bien desde la antigüedad, tanto la resolución de ecuaciones algebraicas asimismo como la determinación de las raíces de los polinomios fueron las máximas preocupaciones a resolver por la matemática, la práctica notación de los mismos y que se usa actualmente, recién aparecería para establecerse hasta nuestros días durante el siglo XV.

Se denomina funciones polinómicas a aquellas que surgirán de evaluar los polinomios sobre las variables a partir de las cuales fueron definidos y así nos encontramos con las siguientes funciones polinómicas: función polinomica de grado 0, función polinómica de grado 1, función polinómica de grado 2, función polinómica de grado 3, y función polinómica de grado 4.

En la práctica ya, los polinomios pueden ser sumados y restados agrupando los términos y simplificando los monomios que presentan semejanzas. En tanto, para multiplicar los polinomios, la metodología será multiplicar cada término de monomio por el otro monomio y nuevamente se simplificarán los monomios semejantes, en un paso posterior.