Definición de Potencia

Ingeniera Industrial, MSc en Física, y EdD
En Matemática, el término potencia indica una forma de expresa un valor, formado por una base y un exponente, el cual indica la cantidad de veces que se debe multiplicar la base por sí misma. La potencia, en Física, expresa la capacidad que posee un cuerpo o sistema físico para consumir o disipar energía por cada unidad de tiempo, y dicha energía puede ser en forma de calor, de sonido, luminosidad, energía nuclear, etc. No se debe confundir el término potencia con el de fuerza, ya que si bien es cierto que para producir un trabajo se requiere la aplicación de una fuerza, estos conceptos no son sinónimos.
Desde el punto de vista físico, la potencia es una cantidad escalar que representa el trabajo realizado por un cuerpo o una carga en una unidad de tiempo. Sus unidades en el Sistema Internacional son watts o Vatios (W), que equivale a Joule sobre segundo (1 W = 1 J/s).
\(P = \frac{T}{t}\)
Donde:
P: potencia (w)
T: trabajo (J)
t: tiempo (s)
La potencia acústica se refiere a la energía que puede emitir un equipo de sonido en forma de ondas sonoras, por cada unidad de tiempo, determinándose a partir del cáclculo de la presión que ejercen las ondas sonoras en el medio de propagación en un instante de tiempo.

Potencia mecánica
La potencia mecánica se determina cuando el trabajo realizado por el cuerpo es de tipo mecánico, por ejemplo, el trabajo realizado por el motor de un vehículo, o el que ejerce una grúa para izar una carga, o el trabajo que realiza una persona al empujar una caja a lo largo de una superficie.
En ocasiones, no se conoce el trabajo mecánico que realiza el cuerpo, pero sí la fuerza que aplica y la velocidad que desarrolla como consecuencia de esa fuerza; en ese caso, la potencia mecánica se determina a partir de la fuerza y la velocidad, partiendo del cálculo de la potencia promedio (Pprom) en un intervalo de tiempo pequeño:
\({P_{prom}} = \frac{T}{{Δt}}\)
Para obtener la potencia instantánea, se evalúa en esta ecuación el límite cuando Δt tiende a cero:
\(P = \mathop {\lim }\limits_{Δt \to o} \frac{T}{{Δt}} = \frac{{dT}}{{dt}}\)
Como el trabajo T efectuado por una fuerza constante se obtiene multiplicando escalarmente la fuerza por el desplazamiento, se tiene:
\(P = \vec F \cdot \frac{{d\vec r}}{{dt}}\)
Donde:
\(d\vec r\): es el vector diferencial de desplazamiento
Finalmente, el cambio de posición con respecto al tiempo representa la velocidad, por lo tanto, la potencia mecánica se puede calcular a partir de los vectores fuerza y velocidad:
\(P = \vec F \cdot \vec v\)
Donde:
\(\vec F\): fuerza aplicada (N)
\(\vec v\): velocidad (m/s)
Ejemplo: Se desea conocer la potencia ejercida por el motor de un elevador que tiene una masa de 2,000 kg y que a su vez sube a unos pasajeros que poseen una masa en conjunto de 180 kg a una velocidad de 2 m/s. También se sabe que durante la trayectoria del elevador, actúa una fuerza de fricción constante equivalente a 2,200 N.
Solución: El primer paso consiste en realizar un análisis dinámico para determinar la fuerza que aplica el motor del ascensor a través de guayas que se encargan de subir y bajar al mismo; para esto, se parte del diagrama de cuerpo libre del elevador:
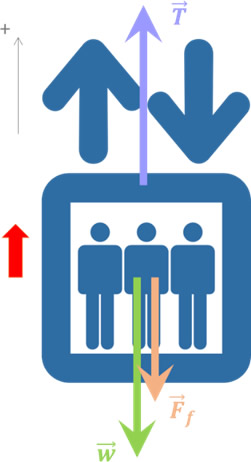
Las fuerzas que actúan sobre el elevador son el peso (del elevador más los pasajeros), la fuerza de fricción y la tensión.
Como el sistema sube a velocidad constante, se aplica la primera ley de Newton:
\(\sum {F_y} = 0\)
\(T – w – {F_f} = 0\)
Al despejar la tensión y sustituir los datos se tiene:
\(T = \left( {2,000 + 180} \right)9.8 + 2,200\)
\(T = 23,564\;N\)
Esta fuerza es vertical con sentido ascendente al igual que el vector velocidad. La potencia del motor resulta:
\(P = \left( {23,564\;N} \right)\hat j \cdot \left( {2\;{\raise0.7ex\hbox{$m$} \!\mathord{\left/
{\vphantom {m s}}\right.\kern-\nulldelimiterspace}
\!\lower0.7ex\hbox{$s$}}} \right)\hat j = 47,128\;W\)
Potencia eléctrica
Cuando se hace referencia a la potencia eléctrica, significa que es el trabajo realizado por la energía eléctrica por cada unidad de tiempo.
Esta definición se puede aplicar a circuitos eléctricos, en los equipos electrónicos, las líneas de transporte y distribución eléctrica, subestaciones eléctricas o cualquier dispositivo que opere con electricidad. Uno de los circuitos más básicos y sencillos de analizar son los circuitos eléctricos resistivos, en los cuales se conozca la intensidad de corriente (i), el voltaje (V) y la resistencia (R). Las expresiones que permiten calcular la potencia a partir de estos parámetros son:
\(P = V \cdot i\)
\(P = {i^2} \cdot R\)
\(P = \frac{{{V^2}}}{R}\)
Donde:
R: resistencia eléctrica ()
i: intensidad de corriente (A)
V: voltaje (V)
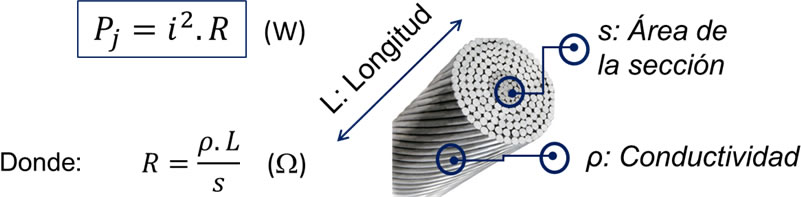
Debido a la circulación de corriente por un conductor que presenta una determinada resistencia (R), se presentan pérdidas por calor Pj (Efecto Joule).
En sistemas eléctricos más complejos donde existen motores eléctricos y máquinas con bobinas, aparecen efectos de inducción, los cuales ocasionan que la potencia que se suministra al sistema (potencia aparente “S”), no se encuentra disponible en su totalidad para el funcionamiento de los elementos del sistema. En esos casos, la potencia se divide en sus componentes, los cuales se muestran en el siguiente triángulo de potencias:
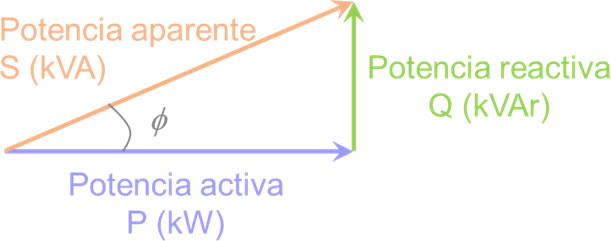
La potencia activa “P” representa la potencia útil del sistema.
El factor de potencia (f.d.p.), es un parámetro adimensional que indica la capacidad de un dispositivo o sistema para convertir la potencia de entrada en potencia útil, por lo tanto, cuanto más se aproxime a la unidad el factor de potencia, más eficiente será el sistema (Φ ⟶ 0).
\(f.d.p. = \frac{P}{S} = cos\;\;\left( {\frac{{kW}}{{kVA}}} \right)\)

Art. actualizado: Nov. 2022; sobre el original de junio, 2009.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.