Significado de potencial eléctrico Definición, ejemplos, carga puntual, y ejercicio

Licenciada en Física
Definición formal
El potencial eléctrico constituye una propiedad del campo eléctrico que se define como la energía potencial por unidad de carga en un determinado punto.

Sea una carga eléctrica de prueba de signo positivo, llamada qo, cuando esta carga se encuentra en el campo, experimenta un potencial eléctrico V dado por
\(V=\frac{{{U}_{E}}}{{{q}_{o}}}\)
Donde UE es la energía potencial electrostática. La unidad de V en el Sistema Internacional de Unidades es el J/C (joule por coulomb), llamada voltio o volt, en honor a Alessandro Volta (1745-1827), inventor de la pila eléctrica. Por este motivo, al potencial eléctrico se le conoce simplemente como voltaje.
Es importante destacar que el potencial eléctrico, al ser energía por unidad de carga, no depende del valor de la carga de prueba, sino que es una propiedad del campo. Tiene la ventaja de ser una cantidad escalar, a diferencia del campo eléctrico, que es vectorial, y esto significa que el potencial eléctrico no tiene dirección ni sentido, lo que facilita los cálculos.
Otro detalle muy importante es que, aunque se habla de potencial eléctrico, en realidad lo que importa desde el punto de vista físico es su variación, relacionada a su vez con la energía potencial eléctrica. Esta siempre se mide respecto a un punto de referencia, tal como se hace con la energía potencial gravitatoria cuando se afirma que en el suelo la energía potencial es 0.
Al hablar de potencial eléctrico, usualmente se define el potencial cero en algún lugar determinado, como por ejemplo el infinito u otro punto específico, dependiendo de la configuración.
Ejemplos de potenciales eléctricos
Pilas
En las pilas o baterías existe un potencial eléctrico que impulsa las cargas eléctricas a través de un circuito cuando este se cierra, de esta forma, la corriente eléctrica produce algún efecto de interés, como encender una linterna, mover un juguete, prender un automóvil o cargar un dispositivo.
El cuerpo humano
Los músculos en el cuerpo humano, incluyendo al corazón, se contraen gracias a pequeños potenciales eléctricos que se producen en células especializadas. Las señales eléctricas viajan a través de los nervios hasta el centro de comando que es el cerebro, y este envía señales eléctricas al resto del cuerpo para que se produzca la acción.
Potencial eléctrico de una carga puntual
Una carga puntual Q es el caso más simple de calcular, la cual produce un campo eléctrico que depende de la distancia radial a la carga, llamada “r”. Sea una carga de prueba qo, que se mueve en este campo, desde un punto arbitrario A hasta otro punto B. La fuerza que ejerce Q sobre qo depende de “r” y de repulsión si las cargas tienen el mismo signo, o de atracción si tienen signos contrarios (la carga de prueba es positiva siempre).
De acuerdo a la ley de Coulomb, la magnitud de esta fuerza es
\(F=k\frac{Q{{q}_{o}}}{{{r}^{2}}}\)
Donde k es la constante electrostática cuyo valor es ≈ 9×109 N∙m2/C2.
Esta fuerza es variable, ya que “r” toma cualquier valor, pero el trabajo solo depende de los desplazamientos radiales rA y rB, ya que la fuerza electrostática es conservativa.
Por lo tanto, el trabajo realizado para ir desde rA hasta rB es
\(W=\underset{{{r}_{A}}}{\overset{{{r}_{B}}}{\mathop \int }}\,k\frac{Q{{q}_{o}}}{{{r}^{2}}}dr=kQ{{q}_{o}}\underset{{{r}_{A}}}{\overset{{{r}_{B}}}{\mathop \int }}\,\frac{dr}{{{r}^{2}}}=~kQ{{q}_{o}}\left( -\frac{1}{r} \right)_{{{r}_{A}}}^{{{r}_{B}}}=-kQ{{q}_{o}}\left( \frac{1}{{{r}_{B}}}-\frac{1}{{{r}_{A}}} \right)\)
Como W = −ΔU, entonces
\(\text{ }\!\!\Delta\!\!\text{ }U=kQ{{q}_{o}}\left( \frac{1}{{{r}_{B}}}-\frac{1}{{{r}_{A}}} \right)\)
Escogiendo UA = 0, cuando rA →∞, y UB = U cuando rB = r, queda
\(U=\frac{kQ{{q}_{o}}}{r}\)
Esta es la energía potencial del sistema de dos cargas Q y qo cuando esta se encuentra a una distancia radial “r” de la carga Q. Para tener el potencial producido por Q en el punto r, basta con dividir el resultado anterior por qo
\(V=\frac{kQ}{r}\)
Obsérvese que el potencial solamente depende de Q y por supuesto, de la distancia radial “r” a la que se encuentre el punto donde se lo quiere hallar.
Potencial producido por una distribución de cargas puntuales
El resultado anterior es una cantidad escalar, que puede ser positiva o negativa según el signo de Q.
Si se tienen “n” cargas puntuales, el potencial neto en un determinado punto es la suma algebraica de los potenciales producidos por cada una de ellas
\(V=\underset{i=1}{\overset{n}{\mathop \sum }}\,\frac{k{{q}_{i}}}{{{r}_{i}}}\)
Ejercicio práctico
Se tiene la distribución de cargas puntuales mostrada en la figura. ¿Cuál es el potencial eléctrico en el punto P?
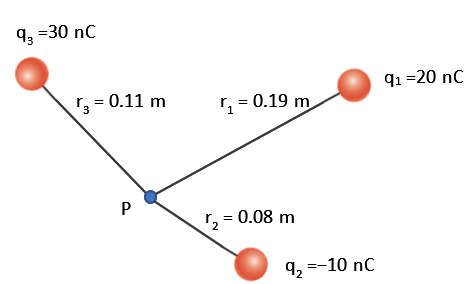
Respuesta
Se trata de una distribución de cargas puntuales, por lo que el potencial en el punto P es
\(V=\underset{i=1}{\overset{n}{\mathop \sum }}\,\frac{k{{q}_{i}}}{{{r}_{i}}}\)
Sustituyendo valores numéricos
\(V=k\left( \frac{{{q}_{1}}}{{{r}_{1}}}+\frac{{{q}_{2}}}{{{r}_{2}}}+\frac{{{q}_{3}}}{{{r}_{2}}} \right)=9\times {{10}^{9}}\left( \frac{20\times {{10}^{-9}}}{0.19}-\frac{10\times {{10}^{-9}}}{0.08}+\frac{30\times {{10}^{-9}}}{0.11} \right)V=2277~V\)

Trabajo publicado en: May., 2021.
Ilustraciones: amnarj2006