Significado de campo eléctrico Definición, fórmula, y ejercicio

Licenciada en Física
Definición formal
El campo eléctrico es la influencia que ejercen los objetos con carga sobre el espacio que los rodea y que perciben otros objetos asimismo cargados.
Surge de la mente del físico inglés Michael Faraday para explicar la interacción entre las cargas eléctricas, la cual es de acción a distancia y no precisa de un medio material para que ocurra.
Fórmula: Explicación de la composición
Para representar el campo eléctrico originado por una carga puntual q, se necesita de una carga de prueba positiva qo, la cual se va colocando en varios puntos alrededor de q. La carga q ejerce una fuerza de repulsión Fo sobre la carga de prueba, como se muestra en la siguiente figura:
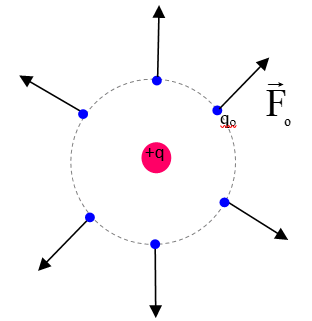
La intensidad o magnitud del campo eléctrico \(\vec{E}\)se define como el límite cuando qo tiende a 0, del cociente entre la magnitud de \({{\vec{F}}_{o}}\)y la carga de prueba qo:
\(E=\underset{{{q}_{o}}\to 0}{\mathop \lim }\,\frac{{{F}_{o}}}{{{q}_{o}}}\)
La idea de tomar el límite es hacer que la carga de prueba sea lo suficientemente pequeña como para no alterar apreciablemente el campo eléctrico propio de q, el cual se busca determinar. Ahora bien, la ley de Coulomb para las cargas puntuales dice que la fuerza entre las cargas q y qo, separadas una distancia r, viene dada por:
\(\vec{F}=k\frac{q{{q}_{o}}}{{{r}^{2}}}\hat{r}\)
Donde k es la constante electrostática, cuyo valor es aproximadamente 9 × 109 N.m2/C2.
La fuerza está dirigida a lo largo de la línea que une a las cargas, lo que se indica mediante \(\hat{r}\), es repulsiva cuando estas son del mismo signo y atractiva cuando son de signos contrarios.
Sustituyendo la magnitud de la fuerza en la definición de campo se obtiene:
\(E=\underset{{{q}_{o}}\to 0}{\mathop \lim }\,\frac{{{F}_{o}}}{{{q}_{o}}}=\underset{{{q}_{o}}\to 0}{\mathop \lim }\,\frac{k\frac{q{{q}_{o}}}{{{r}^{2}}}}{{{q}_{o}}}=k\frac{q}{{{r}^{2}}}\)
El resultado establece que el campo eléctrico producido por una carga puntual positiva, a una distancia r, es directamente proporcional a la magnitud de la carga q e inversamente proporcional al cuadrado de r, la distancia que hay entre la carga y el punto donde se quiere calcular el campo. La dirección del campo es radial con la carga y el sentido es saliente a la carga.
En cuanto al campo eléctrico de una carga negativa, el procedimiento se repite usando la carga de prueba positiva. En este caso la fuerza es de atracción y el campo eléctrico tiene sentido entrante a la carga negativa, como se ve en el siguiente diagrama:
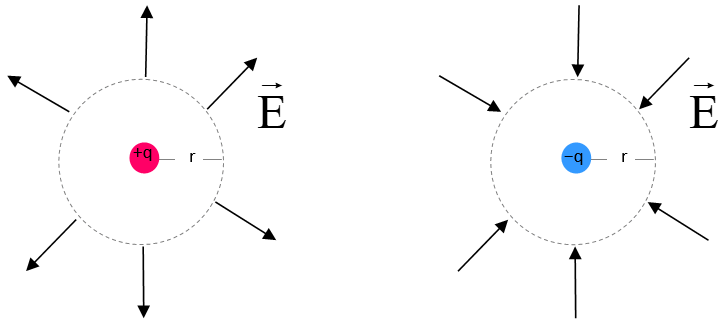
El vector campo eléctrico y sus unidades
En forma vectorial y de acuerdo a lo antes dicho, el campo eléctrico \(\vec{E}\)se escribe como:
\(\vec{E}=k\frac{q}{{{r}^{2}}}\hat{r}\)
Donde q es la carga puntual que lo produce, r es la distancia entre la carga y el punto P de interés, k es la constante electrostática y \(\hat{r}\) el vector unitario (de módulo igual a 1) en la dirección de la línea que une a la carga con P.
Y dado que el campo se define como fuerza por unidad de carga, su unidad en el Sistema Internacional de unidades SI es newton/coulomb o N/C en forma abreviada. Otra unidad que también es de uso frecuente y que lo relaciona con el potencial eléctrico es el voltio/metro o V/m.
Campo eléctrico de distribuciones de cargas puntuales
La expresión anterior es válida para el campo producido por una sola carga puntual en una ubicación determinada.
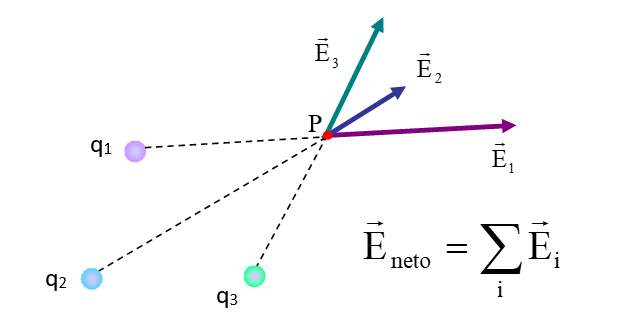
Si se tiene un conjunto de cargas puntuales o distribución, el campo eléctrico resultante es la suma vectorial del campo producido por cada una de las cargas:
\(\,{{\vec{E}}_{neto}}={{\vec{E}}_{1}}+{{\vec{E}}_{2}}+{{\vec{E}}_{3}}+…\)
Caso de Ejercicio
Hallar el vector campo eléctrico en el centro del cuadrado de lado a = 5 cm mostrado en la figura, si
q =2.5 × 10-3 C.
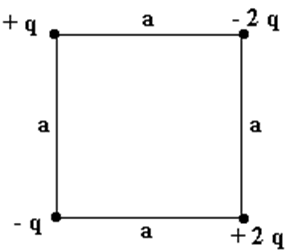
Respuesta
Esta es una distribución de cargas discretas, es decir, cada carga contribuye al campo eléctrico en el punto de interés. Pero antes de aplicar la ecuación para calcular el campo de cada una, es necesario hacer un esquema de los campos en el punto de interés, que es el centro del cuadrado O.
El diagrama se dibuja recordando que el campo producido por una carga positiva es saliente a ella en el punto, mientras que el de una carga negativa es entrante. Además, la longitud del vector es proporcional a la magnitud de la carga, por lo tanto, en la figura se ha procurado dibujarlos a escala, al menos en lo que respecta a la proporción entre ellos.
Asimismo las cargas se numeraron en sentido horario para identificar fácilmente los campos que cada una produce. Como hay algunas tienen el doble de magnitud, su campo se dibuja con una flecha del doble de largo. El esquema que resulta es como sigue:

Se adjunta también un sistema de referencia que es necesario establecer al resolver problemas de campo eléctrico, ya que este es un vector y hay que especificar no solamente magnitud, sino dirección y sentido.
El dibujo muestra simetrías que se pueden aprovechar para simplificar los cálculos. Por ejemplo, al sumar vectorialmente los vectores \({{\vec{E}}_{1}}\) y \({{\vec{E}}_{4}}\), que tienen el mismo módulo, sus componentes horizontales se cancelan por ser opuestas, y se suman únicamente las componentes verticales, que se dirigen hacia abajo y por ellos se distinguen con signo negativo.
Algo parecido sucede al sumar vectorialmente \({{\vec{E}}_{2}}\)y \({{\vec{E}}_{3}}\), las respectivas componentes horizontales se cancelan mientras que las verticales, dirigidas hacia arriba (con signo positivo), se suman. Por este motivo, solamente se calcularán componentes verticales de cada campo, que se obtienen multiplicando por cos 45º (ver el ángulo en la figura y el sistema de referencia adjunto a la derecha).
En cuanto a la distancia entre las cargas y el centro del cuadrado, es la misma para todas: la mitad de la diagonal D, que se calcula con teorema de Pitágoras:
\(D=\sqrt{2\times {{\left( {{5.10}^{-2}}m \right)}^{2}}}=0.0707m\)
\({{d}_{1}}={{d}_{2}}={{d}_{3}}={{d}_{4}}=\frac{D}{2}=0.035m\)
Las respectivas componentes de cada campo son:
\({{E}_{1y}}={{E}_{4y}}=\frac{k{{q}_{1}}}{d_{1}^{2}}(-\cos 45{}^\text{o})=9\times {{10}^{9}}\frac{2.5\times {{10}^{-3}}}{{{\left( 0.035 \right)}^{2}}}(-\frac{\sqrt{2}}{2})\frac{N}{C}=-1.04\times {{10}^{10}}\frac{N}{C}\)
\({{E}_{2y}}={{E}_{3y}}=\frac{k{{q}_{2}}}{d_{1}^{2}}(+\cos 45{}^\text{o})=9\times {{10}^{9}}\frac{2\times 2.5\times {{10}^{-3}}}{{{\left( 0.035 \right)}^{2}}}(+\frac{\sqrt{2}}{2})\frac{N}{C}=+2.08\times {{10}^{10}}\frac{N}{C}\)
Finalmente, la magnitud del campo neto es la suma algebraica:
Eneto = E1y + E2y +E3y + E4y =
= −1.04 × 1010 −1.04 × 1010 + 2.08 × 1010+ 2.08 × 1010 N/C = +2.08 × 1010 N/C
Y en forma vectorial, el resultado es:
\({{\vec{E}}_{neto}}=2.08\times {{10}^{10}}\frac{N}{C}(\hat{y})\)

Trabajo publicado en: Ene., 2021.