¿Qué son las Ecuaciones de Maxwell, y cómo se definen?

Ángel Zamora Ramírez
Licenciado en Física

Las ecuaciones de Maxwell son un conjunto de expresiones matemáticas que logran unificar los fenómenos eléctricos y magnéticos en uno solo llamado “electromagnetismo”. Estas elegantes y sofisticadas ecuaciones fueron publicadas por el matemático James Clerk Maxwell en 1864.

Anterior a estas ecuaciones se decía que las fuerzas eléctricas y magnéticas eran “fuerzas a distancia”, no se conocía ningún medio físico por medio del cual se dieran este tipo de interacciones. Después de muchos años de investigación sobre electricidad y magnetismo, Michael Faraday intuía que tendría que existir algo físico en el espacio entre las cargas y las corrientes eléctricas que les permitiera interactuar entre sí y manifestar todos los fenómenos eléctricos y magnéticos que se conocían, él en un principio se refirió a esto como “líneas de fuerza”, lo cual llevó a la idea de la existencia de un campo electromagnético.

Basándose en la idea de Faraday, James Clerk Maxwell desarrolla una teoría de campos representada por cuatro ecuaciones diferenciales parciales. Maxwell se refirió a esto como “teoría electromagnética” y fue el primero en incorporar este tipo de lenguaje matemático en una teoría física. Las ecuaciones de Maxwell en su forma diferencial para el vacío (Es decir, en ausencia de materiales dieléctricos y/o polarizables) son las siguientes:

\(\nabla \cdot \vec{E}=\frac{\rho }{{{\epsilon }_{0}}}\)
\(\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\)
\(\nabla \cdot \vec{B}=0\)
\(\nabla \times \vec{B}={{\mu }_{0}}\vec{J}+{{\mu }_{0}}{{\epsilon }_{0}}\frac{\partial \vec{E}}{\partial t}\)
Ecuaciones de Maxwell para el vacío en su forma diferencial

Donde \(\vec{E}~\)es el campo eléctrico, \(\vec{B}~\)es el campo magnético, \(\rho ~\)es la densidad de carga eléctrica, \(\vec{J}~~\)es un vector asociado a una corriente eléctrica, \({{\epsilon }_{0}}~\)es la permitividad eléctrica del vacío y \({{\mu }_{0}}~~\)es la permeabilidad magnética del vacío. Cada una de estas ecuaciones corresponde a una ley del electromagnetismo y tiene un significado. A continuación, explicaré brevemente cada una de ellas.

Ley de Gauss

\(\nabla \cdot \vec{E}=\frac{\rho }{{{\epsilon }_{0}}}\)
Ley de Gauss para el campo eléctrico

Esta primera ecuación lo que nos dice es que las cargas eléctricas son las fuentes del campo eléctrico, este campo eléctrico “diverge” directamente de las cargas. Además, la dirección del campo eléctrico está dictada por el signo de la carga eléctrica que lo produce y el qué tan juntas están las líneas de campo indica la magnitud del campo en sí. La imagen de abajo resume de cierta manera lo que se acaba de mencionar.

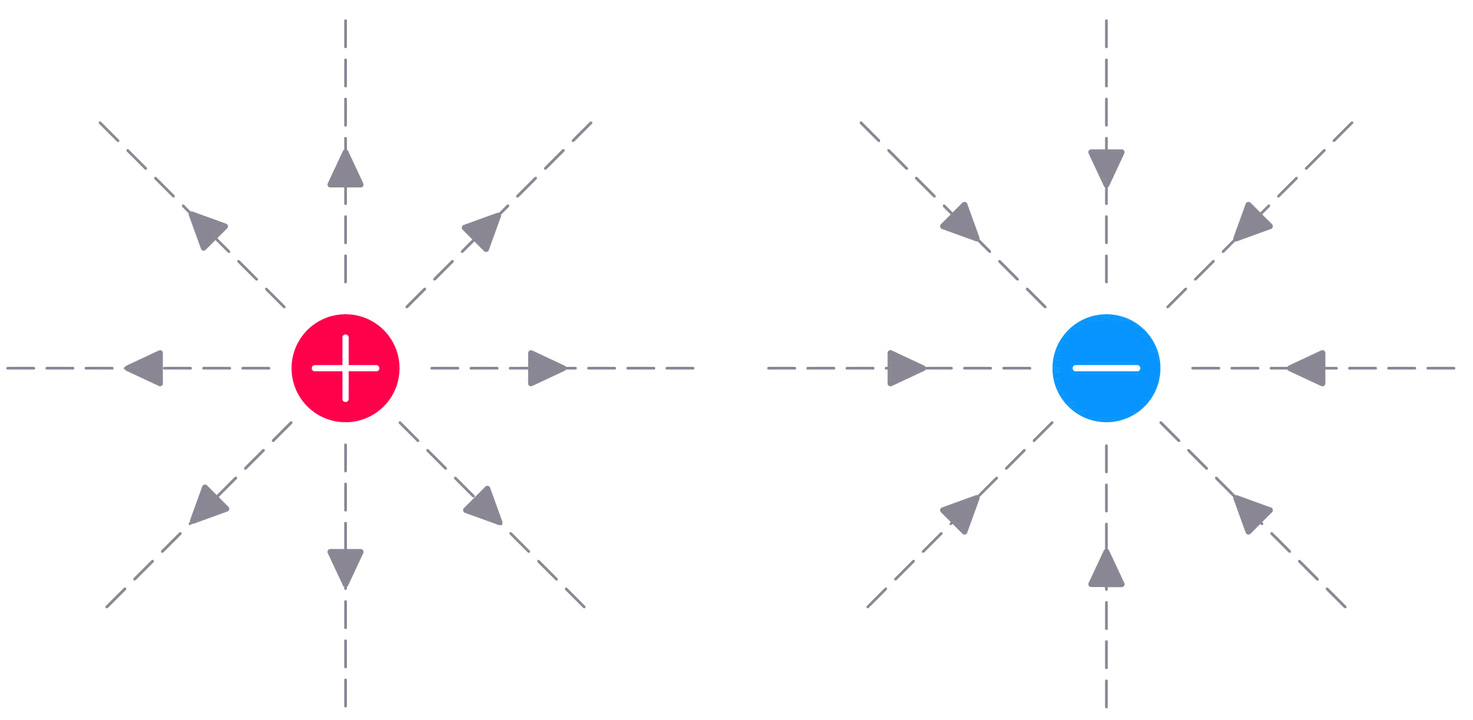
Ilustración 1.De Studiowork.- Esquema de los campos eléctricos generados por dos cargas puntuales, una positiva y otra negativa.

Esta ley debe su nombre al matemático Johann Carl Friedrich Gauss quién la formuló basándose en su teorema de divergencia.

Ley de Gauss para el campo magnético

\(\nabla \cdot \vec{B}=0\)

Esta ley no tiene un nombre en específico, pero se le llama así por su similitud con la ecuación anterior. El significado de esta expresión es que no hay una “carga magnética” análoga a la “carga eléctrica”, es decir, no existen monopolos magnéticos que sean la fuente del campo magnético. Esta es la razón por la cual si partimos un imán a la mitad seguiremos teniendo dos imanes similares, ambos con un polo norte y un polo sur.

Ley de Faraday

\(\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\)
Ley de inducción de Faraday

Esta es la famosa ley de inducción formulada por Faraday cuando en 1831 descubrió que campos magnéticos variables eran capaces de inducir corrientes eléctricas. Lo que significa esta ecuación es que un campo magnético que cambia con el tiempo es capaz de inducir alrededor de este un campo eléctrico, el cual a su vez puede hacer que cargas eléctricas se muevan y crear una corriente. Aunque en un principio esto puede sonar muy abstracto, la ley de Faraday está detrás del funcionamiento de los motores, las guitarras eléctricas y las parrillas de inducción.

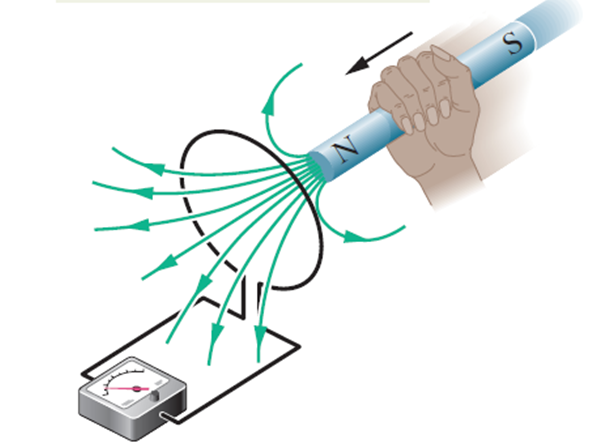
Ilustración 2.- Manifestación de la Ley de Faraday. Un amperímetro registra una corriente eléctrica en un circuito cerrado cuando un imán se mueve respecto a este.

Ley de Ampère – Maxwell

\(\nabla \times \vec{B}={{\mu }_{0}}\vec{J}+{{\mu }_{0}}{{\epsilon }_{0}}\frac{\partial \vec{E}}{\partial t}\)

Lo primero que nos dice esta ecuación es que las corrientes eléctricas generan campos magnéticos alrededor de la dirección de la corriente y que de la magnitud de esta depende la magnitud del campo magnético generado, esto fue lo que observó Oersted y que posteriormente Ampère pudo formular. Sin embargo, hay algo curioso detrás de esta ecuación, y es que, el segundo término que se encuentra del lado derecho de la ecuación fue introducido por Maxwell debido a que esta expresión originalmente era inconsistente con las demás, particularmente, llevaba a una violación de la ley de conservación de la carga eléctrica. Para evitar esto Maxwell simplemente introdujo este segundo término para que toda su teoría fuera consistente, este término recibió el nombre de “corriente de desplazamiento” y en su momento no había ninguna evidencia experimental que lo respaldara.

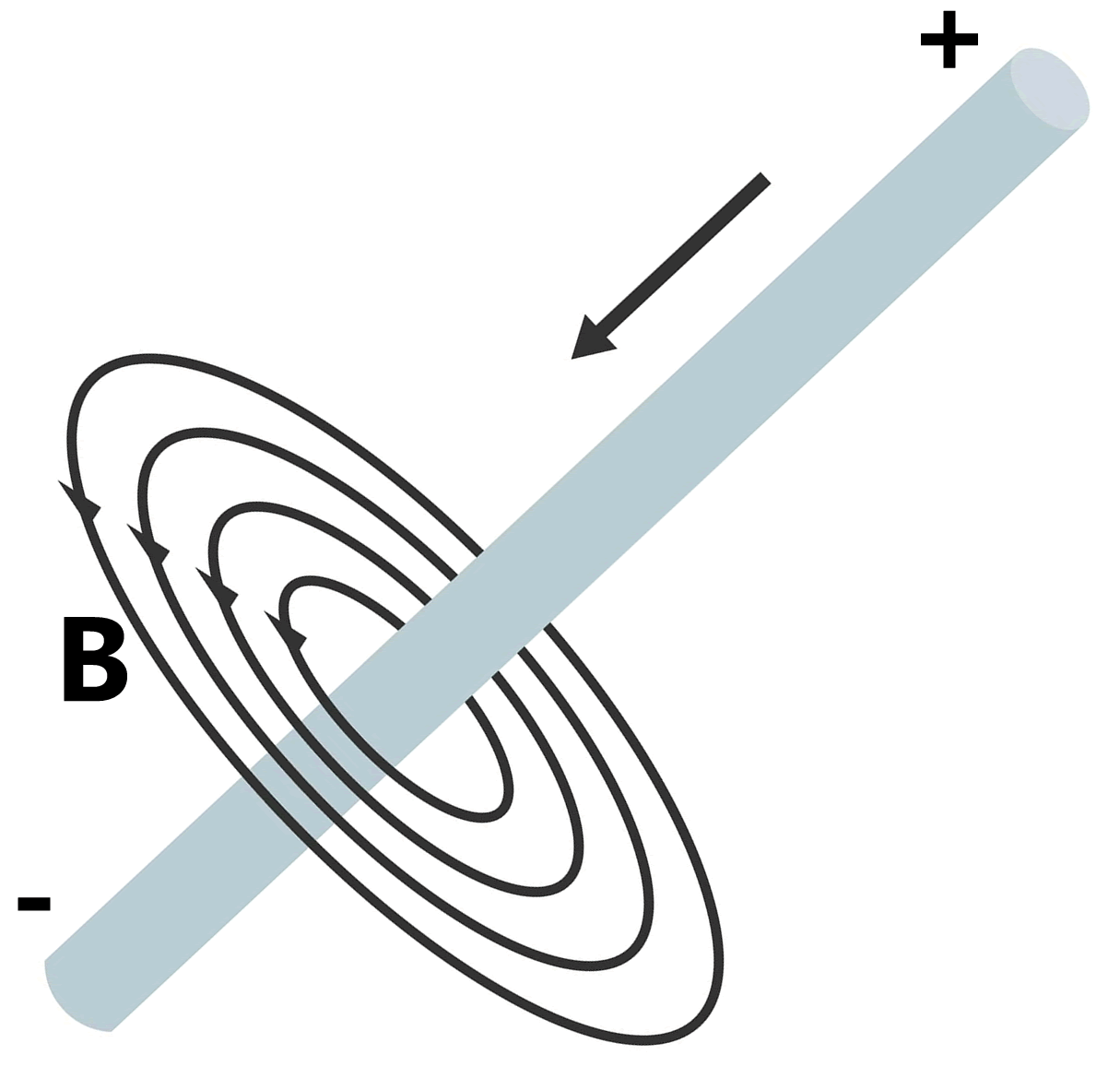
Ilustración 3. De Rumruay.- Una corriente eléctrica circulando por un cable genera un campo magnético alrededor de este de acuerdo a la Ley de Ampère.

El significado de la corriente de desplazamiento es que, de la misma manera en que un campo magnético variable induce un campo eléctrico, un campo eléctrico que cambia con el tiempo es capaz de generar un campo magnético. La primera confirmación experimental de la corriente de desplazamiento fue la demostración de la existencia de ondas electromagnéticas por Heinrich Hertz en 1887, más de 20 años después de la publicación de la teoría de Maxwell. No obstante, la primera medición directa de la corriente de desplazamiento fue hecha por M. R. Van Cauwenberghe en 1929.

La luz es una onda electromagnética

Una de las primeras predicciones alucinantes hecha por las ecuaciones de Maxwell es la existencia de ondas electromagnéticas, pero no sólo eso, también revelaron que la luz tenía que ser una onda de este tipo. Para ver de alguna manera esto jugaremos un poco con las ecuaciones de Maxwell, pero antes de eso, a continuación, se presenta la forma de una ecuación de onda cualquiera:

\({{\nabla }^{2}}u=\frac{1}{{{v}^{2}}}\frac{{{\partial }^{2}}u}{\partial {{t}^{2}}}\)
Forma general de una ecuación de onda en tres dimensiones.

Donde \({{\nabla }^{2}}\) es el operador laplaciano, \(u\) es una función de onda y \(v\) es la velocidad de la onda. También trabajaremos con las ecuaciones de Maxwell en el espacio vacío, es decir, en ausencia de cargas eléctricas y corrientes eléctricas, sólo campos eléctricos y magnéticos:

\(\nabla \cdot \vec{E}=0\)

\(\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\)

\(\nabla \cdot \vec{B}=0\)

\(\nabla \times \vec{B}={{\mu }_{0}}{{\epsilon }_{0}}\frac{\partial \vec{E}}{\partial t}\)

Y también utilizaremos la siguiente identidad de cálculo vectorial:

\(\nabla \times \left( \nabla \times \vec{A} \right)=\nabla \left( \nabla \cdot \vec{A} \right)-{{\nabla }^{2}}\vec{A}\)

Si nosotros aplicamos esta identidad a los campos eléctricos y magnéticos utilizando las ecuaciones de Maxwell para el espacio vacío que están arriba, obtenemos los siguientes resultados:

\({{\nabla }^{2}}\vec{E}={{\mu }_{0}}{{\epsilon }_{0}}\frac{{{\partial }^{2}}\vec{E}}{\partial {{t}^{2}}}\)

\({{\nabla }^{2}}\vec{B}={{\mu }_{0}}{{\epsilon }_{0}}\frac{{{\partial }^{2}}\vec{B}}{\partial {{t}^{2}}}\)

Nótese la similitud de estas ecuaciones con la ecuación de onda de hasta arriba, en conclusión, los campos eléctricos y magnéticos pueden comportarse como ondas (ondas electromagnéticas). Si definimos la velocidad de estas ondas como \(c\) y comparamos estas ecuaciones con la ecuación de onda de arriba podemos decir que dicha velocidad es:

\(c=\frac{1}{\sqrt{{{\mu }_{0}}{{\epsilon }_{0}}}}\)

\({{\mu }_{0}}\) y \({{\epsilon }_{0}}\) son la permeabilidad magnética y la permitividad eléctrica del vacío, respectivamente, y ambas son constantes universales cuyos valores son \({{\mu }_{0}}=4\pi \times {{10}^{-7}}~~T\cdot m/A\) y \({{\epsilon }_{0}}=8.8542\times {{10}^{-12}}~{{C}^{2}}/N\cdot m~\), reemplazando estos valores se tiene que el valor de \(c\) es \(c=299,792,458\frac{m}{s}\approx 300,000~km/s\) lo cual es exactamente la velocidad de la luz.

Con este pequeño análisis podemos obtener tres conclusiones muy importantes:

1) Los campos eléctricos y magnéticos pueden comportarse como ondas, es decir, existen ondas electromagnéticas que además son capaces de propagarse por el vacío.

2) La luz es una onda electromagnética cuya velocidad depende de la permeabilidad magnética y la permitividad eléctrica del medio a través del cual se propaga, en el espacio vacío la luz tiene una velocidad aproximada de 300,000 km/s.

3) Como la permeabilidad magnética y la permitividad eléctrica son constantes universales, entonces la velocidad de la luz es también una constante universal, pero también esto implica que su valor no depende del marco de referencia desde el cuál se mida.

Esta última afirmación fue de gran polémica en aquel entonces, ¿Cómo es posible que la velocidad de la luz sea la misma independientemente del movimiento de quién la mide y del movimiento de la fuente de luz? La velocidad de algo tiene que ser relativa ¿No? Bueno, pues esto fue un parteaguas para la física de la época y este simple pero profundo hecho llevó al desarrollo de la Teoría de Relatividad Especial por Albert Einstein en 1905.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Jul., 2022.

Datos para citar en modelo APA: Zamora Ramírez, A. (julio, 2022). Definición de Ecuaciones de Maxwell. Significado.com. Desde https://significado.com/ecuaciones-maxwell/