Significado de sistemas de ecuaciones lineales Definición, y método (reducción, sustitución, igualación, gráfico)

Licenciada en Física
Definición formal
Los sistemas de ecuaciones lineales son agrupaciones de ecuaciones de primer grado con las mismas incógnitas, de los cuales se precisa hallar una solución común. El sistema puede contener m ecuaciones y n incógnitas, y su solución ser única, como también plantear infinitas posibilidades o no tener respuesta.
Los sistemas con solución se denominan sistemas consistentes. Si la solución es única, el sistema es compatible o consistente determinado, los que tienen infinitas soluciones son sistemas consistentes dependientes o compatibles indeterminados y los que no tienen solución son inconsistentes o incompatibles.
Una condición requerida para que exista una solución única es que el sistema tenga al menos n ecuaciones independientes con n incógnitas. Si se tienen menos ecuaciones que incógnitas (m Los sistemas de ecuaciones lineales son frecuentes en muchas aplicaciones, como por ejemplo hallar las corrientes eléctricas que circulan por un circuito resistivo de corriente directa, mezclas de soluciones con distinta concentración y algunas clases de inversiones monetarias, por citar algunas. En general, la forma de un sistema de m ecuaciones lineales y n incógnitas es: Donde los coeficientes a11, a12…, amn son números reales, así como los términos independientes c1, c2, …cm. Un ejemplo de sistema de dos ecuaciones lineales con dos incógnitas es: Tomando este sistema como ejemplo, a continuación se aplican distintos métodos de solución. En este método se busca eliminar una de las variables sumando o restando las ecuaciones. De ser necesario, se multiplican las ecuaciones por números reales apropiados, ya que una ecuación no se altera si se multiplica por la misma cantidad a ambos lados de la igualdad. Para resolver el sistema propuesto, se puede multiplicar la primera ecuación por −5, así: Que resulta en: \(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}} {\text{-5x-10y}=\text{-}35} \\ {\text{5x-y}=\text{2}} \end{array}} \right.\\\text{ }\end{array}\) Las dos ecuaciones se suman término a término, eliminando la incógnita x: \(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}} {\text{-5x-10y}=\text{-}35} \\ {\text{5x-y}=\text{2}} \end{array}} \right.\\\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ }\\\text{ -11y }=\text{ -33}\end{array}\) \(\text{y }=\frac{\text{-33}}{\text{-11}}\) y = 3 Este valor de y se sustituye en alguna de las ecuaciones originales para obtener el valor de x: \(\text{5x-3 }=2\) \(\text{x}=\frac{\text{2}+\text{3}}{\text{5}}\) \(\text{x}=\frac{\text{5}}{\text{5}}\) \(\text{x}= \text{1}\) También se hubiera podido eliminar la y al multiplicar la segunda ecuación por 2 y sumar con el resultado con la primera ecuación. Se deja como ejercicio para el lector comprobar que se obtiene la misma solución. Consiste en despejar una de las incógnitas de una de las ecuaciones y sustituir el despeje en la otra. Se puede escoger cualquiera de las variables y cualquiera de las ecuaciones. En el sistema: Se puede despejar la x de la primera ecuación y sustituirla en la segunda: \(\text{x}=\text{7-2y}\) \(\text{5}\times \text{(7-2y)-y}=\text{2}\) \(\text{35-10y-y }=\text{ 2}\) Como ha quedado una ecuación con una sola incógnita, esta se despeja de la manera habitual: \(\text{-10y-y }=\text{ 2-35}\) \(\text{-11y }=\text{ -33}\) \(\text{y }=\frac{\text{-33}}{\text{-11}}\) y = 3 Este valor de y se sustituye ahora en el despeje de la x que se tiene inicialmente: \(\text{x}=\text{7-2y}\) \(\text{x}=\text{7-2}\times \text{3}=\text{7-6}=\text{1}\) x = 1 El lector puede comprobar que despejando la incógnita y de una ecuación y sustituyendo en la otra se obtiene la misma solución. Para aplicar este método es necesario despejar la misma incógnita en cambas ecuaciones e igualar luego el resultado. Siguiendo con el mismo sistema de los ejemplos anteriores: Al despejar la x de la primera ecuación se tiene: \(\text{x}=\text{7-2y}\) Y la misma variable, despejada de la segunda ecuación es: \(x=\frac{y+2}{\text{5}}\) Ya que ambas son expresiones válidas para x, se pueden igualar sin problema: \(\text{7-2y}=\frac{y+2}{\text{5}}\) Se multiplica a ambos lados de la igualdad por 5 para eliminar el denominador: \(\text{5}\times \text{(7-2y)}=5\times \left( \frac{y+2}{\text{5}} \right)\) \(35-10y=y+2\) Los términos que contienen la incógnita se pasan a la derecha y los términos independientes a la izquierda: \(-10y-y=2-35\) \(\text{-11y }=\text{ -33}\) \(\text{y }=\frac{\text{-33}}{\text{-11}}\) \(y = 3\) El valor de x se encuentra sustituyendo y = 3 en alguna de las ecuaciones originales, por ejemplo: \(\text{x}+\text{2y}=\text{7}\) \(\text{x}+\text{2}\times \text{3}=\text{7}\) \(\text{x}+\text{6}=\text{7}\) \(\text{x}=\text{7-6}=\text{1}\) \(x=1\) Queda como ejercicio para el lector despejar e igualar la incógnita y de ambas ecuaciones para verificar que se obtiene la misma solución. Cada una de las ecuaciones del sistema propuesto corresponde a una recta en el plano, si se grafican ambas rectas se puede determinar su intersección, que es el punto común a ambas y la solución del sistema. De la primera ecuación en el sistema: Se tiene que: \(\text{y }=\text{ }\frac{\text{7}}{\text{2}}-\frac{\text{x}}{\text{2}}\) Y de la segunda: \(\text{y }=\text{ }5\text{x-2}\) La suma de los números que componen una cifra de dos dígitos es 7. Cuando los dígitos se invierten, la cifra aumenta en 27. Hallar la cifra. Solución Una cifra de dos dígitos está compuesta de dos números x e y en ese orden. El enunciado dice que la suma de ambos es 7, por lo tanto, la primera ecuación del sistema es: x + y = 7 Ahora bien, El número x puede tomar valores entre 1, 2, 3… hasta 9, ya que está en la posición de las decenas (la cifra tiene dos dígitos según el enunciado) mientras que y lo hace desde 0 hasta 9. Una cifra compuesta de dos dígitos se puede expresar como: 10x + y Si los dígitos se invierten, la incógnita y pasa a la posición de las decenas y el nuevo número es: 10y + x El enunciado dice que el número con los dígitos invertidos es igual al número original aumentado en 27, por lo tanto: 10y + x= (10x + y) + 27 Escribiendo las variables a la izquierda y los términos independientes a la derecha se tiene: 10y + x -10x-y = 27 -9x + 9y = 27 Que se simplifica a: -x + y = 3 Esta es la segunda de las ecuaciones del sistema, el cual queda: Al sumar las dos ecuaciones la incógnita x se elimina y queda: 2y = 10 y = 5 Despejando x de la primera ecuación y sustituyendo y = 5 queda: x = 7 – y La cifra buscada es 25. Si los números se invierten se obtiene 52 que es igual a la suma de 25 y 27.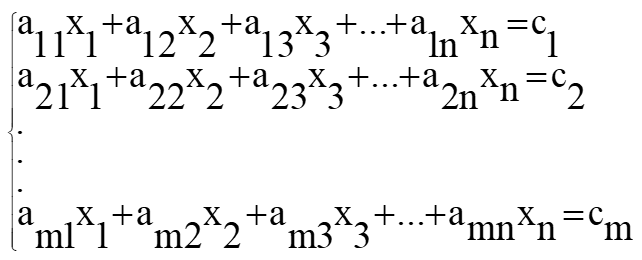
Las incógnitas son x1, x2, x3…xn. Nótese que las ecuaciones lineales no contienen raíces ni potencias de las variables, ni estas son argumento de alguna función trascendente como logaritmos, exponenciales o funciones trigonométricas. 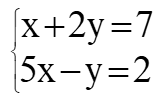
Método de reducción
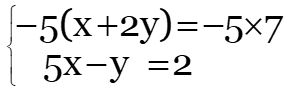
Método de sustitución
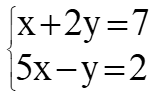
Método de igualación
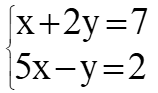
Método gráfico
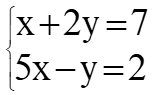
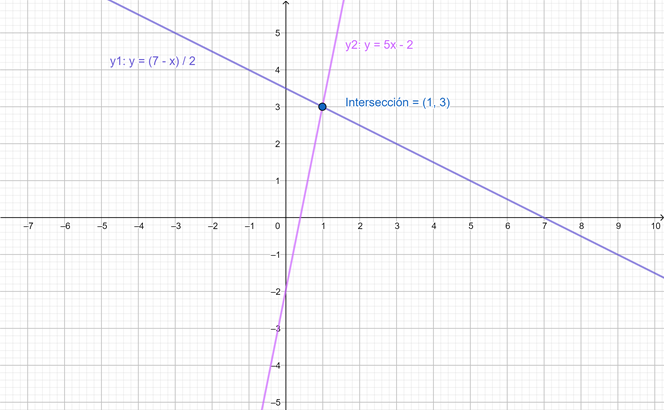
Ejercicio práctico
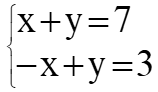
x = 7 – 5 = 2
Trabajo publicado en: Ene., 2021.