Significado de ecuaciones de segundo grado Definición, completas/incompletas, y soluciones

Licenciada en Física
Definición formal
Son fórmulas polinómicas de la forma P(x)=0, donde P(x) es un polinomio de grado 2, por lo que también se las conoce como ecuaciones cuadráticas.
El tipo de estructura matemática queda ilustrada en:
ax2 + bx + c = 0, con a ≠ 0.
Los coeficientes a, b y c son números reales.
Ecuaciones de Segundo Grado Completas e Incompletas (Puras y Mixtas)
Completas: cuando todos los coeficientes a, b y c son distintos de 0, por ejemplo:
2x2 − 4x − 5 = 0
a = 2
b = −4
c = −5
Incompletas: en este caso, a su vez divididas en puras y mixtas.
Ecuaciones incompletas puras carecen del término lineal, es decir, b = 0, por lo tanto son de la forma:
ax2 + c = 0
Por ejemplo:
x2 − 4 = 0
Por su parte, en las ecuaciones incompletas mixtas el término independiente es 0, como aquí:
6x2 + 4x = 0
Las ecuaciones de segundo grado pueden tener 2, 1 o ninguna solución real, pero siempre pueden tener soluciones en el campo de los números complejos. Aparecen con frecuencia en diversos campos de la ciencia, por lo que es muy conveniente conocer los métodos para resolverlas.
Métodos de solución: despeje directo, factorizar, completar cuadrados y fórmula general
Existen varias maneras de solucionar una ecuación de segundo grado, tanto de forma algebraica como gráfica. Algunos métodos algebraicos se pueden aplicar únicamente en las ecuaciones incompletas y otros son válidos para todos los tipos.
Método 1: despeje directo
Se aplica este método en el caso de las ecuaciones de segundo grado incompletas puras.
Ejemplo 1
Hallar la solución de: x2 − 4 = 0
Respuesta
Se despeja la incógnita:
x2 = 4
Y aplicando raíz cuadrada en ambos lados se obtienen dos soluciones:
\(\sqrt{{{x}^{2}}}=\sqrt{4}\)
\(x=\pm 2\)
Método 2: factorizar
Este método se puede aplicar a cualquier ecuación de segundo grado, pero la técnica particular depende del tipo de ecuación. Hace uso de la llamada propiedad del producto 0, la cual expresa que el producto de dos o más factores es 0, cuando al menos uno de ellos es 0. Así:
a∙b = 0
Solamente si a = 0, o si b = 0
Entonces, si se logra factorizar la ecuación, las soluciones se obtienen igualando cada uno de los factores a 0.
Ejemplo 2
Resolver:
6x2 + 4x = 0
Respuesta
Se factoriza la ecuación:
2x∙ (3x+2) = 0
Quedan dos factores, el primero es a = 2x, que cuando se iguala a 0 resulta en la primera solución:
x1 = 0
El segundo factor es: b = 3x+2. Al igualar a 0:
3x+2 = 0
x2 = − 2/3
Ejemplo 3
Hallar, si existen, las soluciones de:
x2 +5x = 24
Respuesta
El primer paso para resolver una ecuación mediante factorización es pasar los términos a un lado de la igualdad e igualar a 0, por lo tanto se reescribe:
x2 +5x − 24 = 0
Ahora se factoriza el trinomio de la siguiente forma:
(x+a)(x+b) = 0
Es decir, hay que encontrar dos números a y b tales que sumados algebraicamente se obtenga 5, y multiplicados den (− 24). Es fácil determinarlos por tanteo o probando, ya que son números pequeños. Por ejemplo:
(−3) x 8 = 24
(−3) + 8 = 5
Por lo tanto la ecuación se puede escribir así:
(x+8)∙(x−3)=0
Seguidamente hay que igualar cada factor a 0 para encontrar las dos soluciones:
x + 8 = 0, x1 = −8
x−3 = 0, x2 = 3
Método 3: completar cuadrados
Mediante algunas manipulaciones algebraicas sencillas, un trinomio se puede completar para expresarlo mediante la suma un trinomio cuadrado perfecto y un término independiente. De esta manera es posible despejar la variable y hallar las soluciones.
Ejemplo 4
Resolver la siguiente ecuación cuadrática completando los cuadrados:
x2 + 8x +7 = 0
Respuesta
El trinomio no se altera si se suma y resta la misma cantidad, además, el término lineal 8x se puede reescribir como 8x = 2∙4x, así que conociendo el producto notable (a+b)2 = a2 +2ab + b2, tiene sentido escoger esa cantidad como 42:
x2 + 2∙4x + 42 −42 + 7 = 0
Nótese que esta expresión equivale exactamente a la original, pero los primeros tres términos constituyen un trinomio cuadrado perfecto:
(x2 + 2∙4x + 42) −42 + 7 = 0
(x+4)2 – 16 + 7 = 0
(x+4)2 = 9
Ahora se aplica raíz cuadrada en ambos lados:
\(\sqrt{{{(x+4)}^{2}}}=\sqrt{9}\)
\(x+4=\pm 3\)
x1 = 3 − 4= −1
x2 = −3 − 4= −7
Método 4: aplicación de la fórmula general
Existe una fórmula general, aplicable a todo tipo de ecuación de segundo grado, la cual también se conoce con el nombre de fórmula resolvente:
\(x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\)
Para determinar las soluciones, simplemente se sustituyen los valores numéricos de los coeficientes a, b y c y se efectúan los cálculos correspondientes.
Discriminante de la ecuación de segundo grado
Nótese que la cantidad:
b2 – 4ac
Se puede utilizar para conocer de antemano si la ecuación tiene raíces reales o no, según estos criterios:
b2 – 4ac > 0: dos soluciones reales y diferentes.
b2 – 4ac = 0, una solución real dada por: x = – b/2a
b2 – 4ac < 0, dos soluciones complejas
Ejemplo 5
Hallar las soluciones de:
2x2 + x – 3 = 0
Respuesta
Los valores a sustituir son:
a = 2, b = 1, c = – 3
Queda:
\(x=\frac{-1\pm \sqrt{{{1}^{2}}-4\times 2\times (-3)}}{2\times 2}=\frac{-1\pm \sqrt{1+24}}{4}=\frac{-1\pm \sqrt{25}}{4}=\frac{-1\pm 5}{4}\)
La primera solución es:
\({{x}_{1}}=\frac{-1+5}{4}=\frac{4}{4}=1\)
Y la segunda:
\({{x}_{2}}=\frac{-1-5}{4}=\frac{-6}{4}=-\frac{3}{2}\)
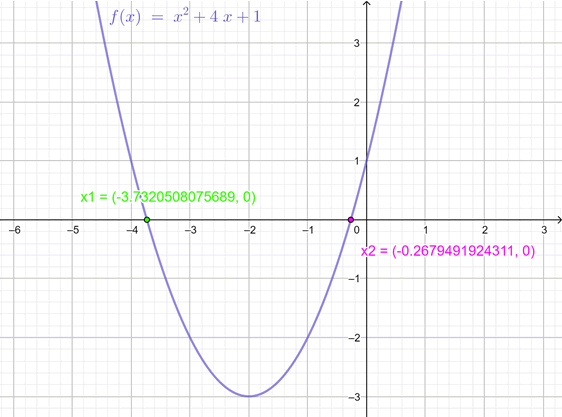
Método 5: a través de la gráfica
Las raíces, o ceros de ax2 + bx + c = 0 son las intersecciones con el eje horizontal de la función cuadrática:
f(x) = ax2 + bx + c
Cuya gráfica es una parábola. Por lo tanto, al graficar f(x) se pueden encontrar sus intersecciones con el eje horizontal y esas son las soluciones reales de la correspondiente ecuación cuadrática. La gráfica de la función se puede hacer fácilmente a través de un software matemático en línea, como Geogebra.
Ejemplo 6
Determinar gráficamente las soluciones de:
x2 + 4x +1 = 0
Respuesta

Trabajo publicado en: Nov., 2020.