Significado de prisma (regular e irregular, recto y oblicuo…) Definición, y características

Licenciada en Física
Definición formal
El prisma es un cuerpo geométrico tridimensional que pertenece a la familia de los poliedros. Cada uno se caracteriza por tener dos bases congruentes y paralelas entre sí, unidas por paralelogramos (cuadrados, rectángulos…) que conforman las caras y cierran la figura. Las caras y las bases se intersectan en segmentos llamados aristas, siendo las aristas laterales los bordes que unen las caras del prisma. Los vértices son las esquinas del mismo, y la altura es el segmento que une a las bases.
Los prismas tienen un amplio uso en el campo de la óptica, por ejemplo, la luz blanca que proviene del Sol se hace pasar por un prisma para observar los distintos colores que la componen, un fenómeno que fue descrito por vez primera por el célebre físico inglés Isaac Newton en su tratado sobre óptica.
Cada color que compone la luz blanca tiene asociada una longitud de onda característica, comenzando con la longitud de onda del rojo: 750 nm hasta la del violeta con 380 nm. Este rango de longitudes de onda es el espectro visible. Los prismas de vidrio transparente con caras triangulares se utilizan mucho para demostrar este efecto.
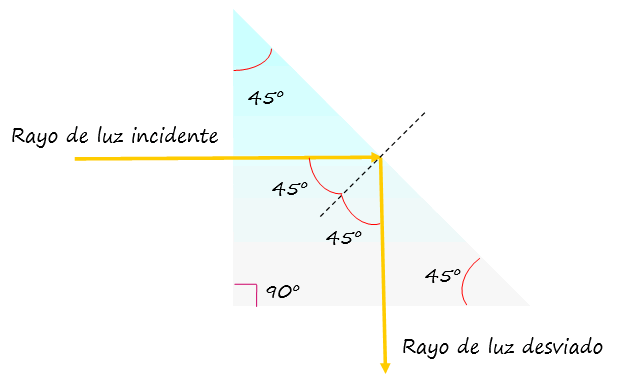
Los primas tienen un amplio uso en dispositivos ópticos como telescopios, microscopios, periscopios, binoculares, espectrómetros y refractómetros, para guiar y desviar a conveniencia los rayos luminosos. Por ejemplo un prisma cortado en ángulos de 45º desvía perpendicularmente un rayo de luz, ya que actúa como un espejo haciendo que la luz se refleje completamente en él, cambiando su dirección en 90º.
En geometría hay diversos criterios para clasificar a los prismas, por ello existen: 1) Regulares e irregulares, 2) Rectos u oblicuos, 3) Triangulares, cuadrangulares, pentagonales, hexagonales, etc. y 4) Convexos y cóncavos
Prismas regulares e irregulares
Las bases de los prismas regulares son polígonos regulares, es decir, polígonos cuyas caras y ángulos internos tienen la misma medida. En cambio, las bases de los prismas irregulares no son polígonos regulares.
La siguiente figura muestra tres prismas regulares: el cubo (morado), el prisma pentagonal (verde) y el prisma hexagonal (fucsia).
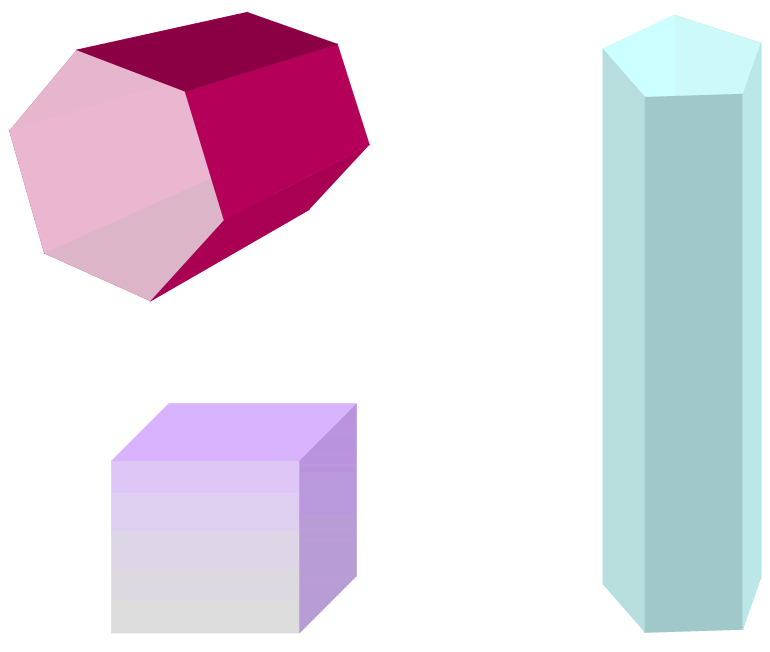
Prismas rectos y oblicuos
La altura del prisma, como se recordará, se define como el segmento perpendicular que va de una base a la otra. Si las aristas laterales del prisma son paralelas a la altura, el prisma es recto y sus caras laterales son rectángulos. En caso contrario, el prisma es oblicuo o inclinado, teniendo sus caras forma de paralelogramo.
Prismas por la forma de sus bases
La forma de la base determina el nombre del prisma, por ejemplo hay prismas triangulares, rectangulares, pentagonales y más. En la figura de arriba el prisma pentagonal tiene caras con forma de pentágono (polígono de 5 lados), mientras que el prisma hexagonal tiene caras con forma de hexágono (polígono de 6 caras).
Prismas convexos y cóncavos
Si la base del prisma es un polígono convexo, es decir, sus ángulos internos son menores a 180º, el prisma es convexo. Los prismas mostrados en las figuras de arriba son convexos. En cambio, si al menos uno de los ángulos internos de la base es mayor de 180º, el prisma es cóncavo.
Cáculo del área superficial del prisma
Para calcular el área superficial del prisma basta con sumar el área de las bases y el área de las caras laterales:
1) \(A={{A}_{bases}}+{{A}_{c}}_{aras}\)
Esta expresión es válida para cualquier tipo de prisma. Sin embargo, hay una fórmula para calcular el área superficial del prisma recto:
2) \(A=2{{A}_{b}}+{{P}_{b}}\cdot h\)
Donde Ab es el área de la base, que depende de la forma de esta, Pb el perímetro de la base y h es la altura del prisma.
En cambio, si el prisma es oblicuo, el área se calcula a través de:
3) \(A=2{{A}_{b}}+{{P}_{r}}\cdot a\)
Aquí Ab sigue siendo el área de la base, pero en vez del perímetro de la base se usa Pr, el perímetro de la sección recta del prisma y en vez de la altura, se emplea la longitud “a” de la arista.
Cáculo del Volumen del prisma
Para cualquier prisma, el volumen se calcula multiplicando el área de la base por la altura:
4) \(V={{A}_{b}}\cdot h\)
Ejercitación
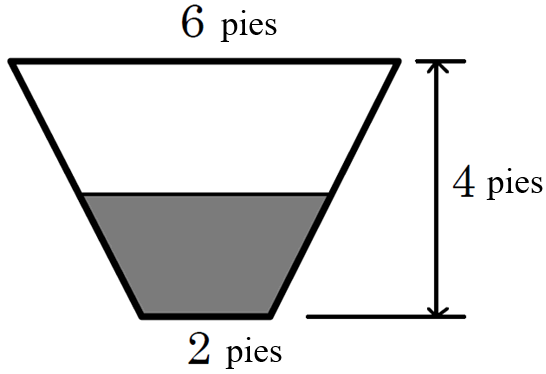
Un depósito para agua tiene forma de prisma trapezoidal de 10 pies de largo, con base en forma de trapecio isósceles. Las medidas de la figura están en pies.
a) ¿Cuál es el volumen del depósito en pies cúbicos y en litros?
b) ¿Cuánta agua hay en el depósito si la altura del líquido es de 2 pies?
Respuestas
a) El depósito tiene forma de prisma trapezoidal recto, es decir, las bases son trapecios, por lo tanto, para calcular el volumen se usa la fórmula 4 dada anteriormente, en la que se debe colocar el área de la base trapezoidal.
El área de un trapecio viene dada por:
\({{A}_{b}}=\frac{1}{2}(B+b)\cdot {{h}_{b}}\)
Donde B = 6 pies representa la base mayor, b= 2 pies es la base menor y hb = 4 pies es la altura del trapecio. Sustituyendo valores:
\({{\text{A}}_{\text{b}}}=\frac{\text{1}}{\text{2}}\text{(B}+\text{b)}\cdot {{\text{h}}_{\text{b}}}=\text{0}\text{.5}\times \text{(6}+\text{2)}\times \text{4 pies cuadrados }=\text{ 16 }{{\text{p}}^{\text{2}}}\)
Ahora se traslada este resultado hasta la fórmula del volumen, donde h es la altura del prisma, que según el enunciado es de 10 pies y queda:
\(\text{V}={{\text{A}}_{\text{b}}}\cdot \text{h}=\text{16}\times \text{10 pies c }\!\!\acute{\mathrm{u}}\!\!\text{ bicos }=\text{ 160 pies c }\!\!\acute{\mathrm{u}}\!\!\text{ bicos}\)
Para expresar el resultado en litros se usa el factor de conversión:
1 pie cúbico = 28.3168L
Por lo tanto, la capacidad en litros del depósito es 4530.7L.
b) El volumen de agua se calcula de la misma forma, pero el área de la base trapezoidal tiene una altura menor, ya que el enunciado dice que la altura del agua es de 2 pies. También la base mayor cambia, pues ya no es de 6 pies sino:
B = 2x + 2
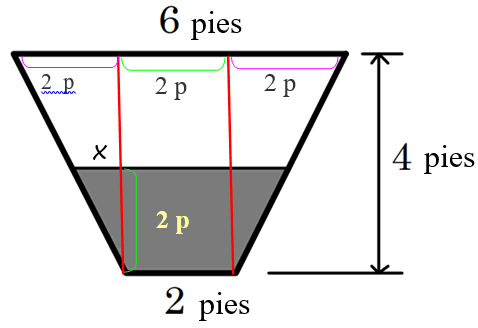
Como se forman triángulos semejantes (ver dibujo), al aplicar el teorema de Thales para despejar el lado “x” resulta:
\(\frac{2}{4}=\frac{x}{2}\Rightarrow x=1\)
Por lo tanto la base mayor del trapecio es B = (2×1 + 2 ) pies = 4 pies. Sustituyendo en la fórmula del área de la base queda:
\({{\text{A}}_{\text{b}}}=\frac{\text{1}}{\text{2}}\text{(B}+\text{b)}\cdot {{\text{h}}_{\text{b}}}=\text{0}\text{.5}\times \text{(4}+\text{2)}\times \text{4 pies cuadrados }=\text{ 12 }{{\text{p}}^{\text{2}}}\)
Y el volumen de agua es:
\(\text{V}={{\text{A}}_{\text{b}}}\cdot \text{h}=\text{1}2\times \text{10 pies c }\!\!\acute{\mathrm{u}}\!\!\text{ bicos }=\text{ 120 pies c }\!\!\acute{\mathrm{u}}\!\!\text{ bicos}\)
Que en litros equivale a 3398.02 L

Trabajo publicado en: Abr., 2021.