Significado de radicación (raíz cuadrada, cúbica…) Definición, ejemplos, y propiedades

Licenciada en Física
Definición formal
La radicación implica identificar la raíz n-ésima de un número o una cantidad algebraica, cuyo resultado es otra cantidad que, elevada al exponente n, permite obtener la representación original.
En notación matemática, la operación de radicación se expresa mediante

A partir de este símbolo, la definición se manifiesta matemáticamente en
\(\sqrt[n]{a}=b\Rightarrow {{b}^{n}}=a\)
Donde a y b son números reales y n pertenece al conjunto de los números naturales N. Cuando n es par, tanto a como b son positivos, luego, no existen raíces pares de cantidades negativas.
Los términos que aparecen en la expresión matemática de radicación comprenden
• Cantidad subradical, es lo que se encuentra dentro del símbolo de raíz, que arriba se representa mediante “a”.
• Raíz n-ésima, es el resultado de extraer la raíz y se denota como “b”
• Índice, el número al cual se eleva la cantidad “b” para obtener la cantidad “a”. Cuando n = 2 no se escribe, porque se entiende que se trata de una raíz cuadrada.
Seguidamente, un ejemplo sencillo aclara el punto
\(\sqrt{16}=4\Rightarrow {{4}^{2}}=16\)
Esta expresión se interpreta de esta forma: la raíz cuadrada de 16 es 4, ya que 4 elevado al cuadrado es 16.
En el siguiente caso, se tiene la raíz cúbica de −729, que es igual a −9, porque −9 elevado a la 3 es igual a −729.
\(\sqrt[3]{\left( -729 \right)}=-9\Rightarrow {{\left( -9 \right)}^{3}}=-729\)
Las raíces mostradas son enteras, pero por lo general, la radicación da como resultado números irracionales, es decir, que tienen una cantidad infinita de decimales no periódicos. Por ejemplo:
\(\sqrt{2}=1.414213562\ldots \)
El lector puede comprobar mediante la calculadora, que
\({{\left( 1.414213562\ldots \right)}^{2}}\cong 2\)
Raíz n-ésima como exponente fraccionario
Una raíz n-ésima se puede escribir como potencia con un exponente fraccionario. El índice de la raíz se escribe en el denominador del exponente, y la potencia de la cantidad subradical pasa como denominador
\(\sqrt[n]{{{a}^{m}}}={{a}^{\frac{m}{n}}}\)
Con n≠0.
Ejemplos
a) \(\sqrt[3]{{{5}^{2}}}={{5}^{\frac{2}{3}}}\)
b) \(\sqrt{y}={{y}^{\frac{1}{2}}}\)
c) \(\sqrt[4]{{{x}^{3}}}={{x}^{\frac{3}{4}}}\)
Simplificación de radicales
Cuando la raíz se expresa como exponente fraccionario, la fracción puede ser propia o impropia. En el primer caso n>m, y en el segundo n
a) \(\sqrt[3]{{{2}^{3}}}={{2}^{\frac{3}{3}}}={{2}^{1}}=2\)
b) \(\sqrt{64}=\sqrt{{{2}^{6}}}={{2}^{\frac{6}{2}}}={{2}^{3}}=8\)
c) \(\sqrt{{{x}^{2}}}={{x}^{\frac{2}{2}}}=x\)
d) \(\sqrt{{{3}^{4}}}={{3}^{\frac{4}{2}}}={{3}^{2}}=9\)
e) \(\sqrt[4]{{{x}^{6}}}={{x}^{\frac{6}{4}}}={{x}^{\frac{3}{2}}}=\sqrt{{{x}^{3}}}=x\sqrt{x}\)
Introducir un factor dentro de un radical
Cuando un factor se encuentra fuera de un radical, es posible hacerlo pasar a a formar parte de la cantidad subradical. Para hacerlo, se escribe el factor dentro de la raíz, pero elevado al índice de dicha raíz, como se muestra seguidamente:
Ejemplos
a) \(2\sqrt{x}=\sqrt{{{2}^{2}}\bullet x}=\sqrt{4x}\)
b) \(x\sqrt{x}=\sqrt{{{x}^{2}}\bullet x}=\sqrt{{{x}^{3}}}\)
c) c)\({{y}^{2}}\sqrt{x}=\sqrt{{{\left( {{y}^{2}} \right)}^{2}}\bullet x}=\sqrt{{{y}^{4}}x}\).
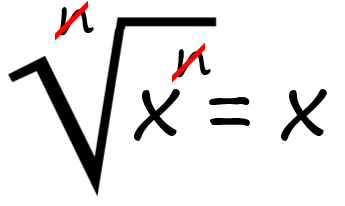
Propiedades de la radicación
1.- Raíz de un producto
La raíz del producto entre dos cantidades “a” y “b” se expresa como:
\(\sqrt[n]{a\bullet b}=\sqrt[n]{a}\bullet \sqrt[n]{b}\)
Ejemplos
a) \(\sqrt[3]{2\bullet 3}=\sqrt[3]{2}\bullet \sqrt[3]{3}\)
b) \(\sqrt[4]{{{x}^{3~}}bullet~{{y}^{2}}}=\sqrt[4]{{{x}^{3}}}\bullet \sqrt[4]{{{y}^{2}}}\)
2.- Raíz de un cociente
El cociente entre dos cantidades “a” y “b”, siempre que b ≠ 0, ya que la división por 0 no está definida, se expresa como:
\(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)
Ejemplos
a) \(\sqrt[4]{\frac{16}{625}}=\frac{\sqrt[4]{16}}{\sqrt[4]{625}}=\frac{2}{5}\)
b) \(\sqrt[3]{\frac{{{x}^{2}}}{{{y}^{3}}}}=\frac{\sqrt[3]{{{x}^{2}}}}{\sqrt[3]{{{y}^{3}}}}=\frac{\sqrt[3]{{{x}^{2}}}}{y}\)
Es importante hacer notar que, en general:
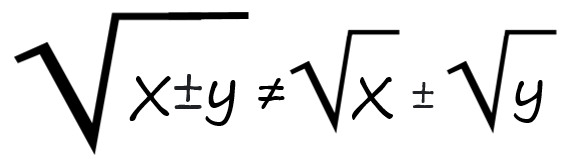
3.- Raíz de una raíz
Para hallar la raíz de una raíz, simplemente se escribe la cantidad subradical dentro una raíz única, cuyo índice es el producto de los índices de las raíces, así:
\(\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\bullet m]{a}\)
Y cuando se tienen sucesivas raíces de raíces, pues se multiplican todos los índices para reducir todo a una sola raíz, como aquí:
\(\sqrt[n]{\sqrt[m]{\sqrt[p]{\sqrt[q]{a}}}}=\sqrt[n\bullet m\bullet p\bullet q]{a}\)
Ejemplos
a) \(\sqrt[4]{\sqrt[3]{7}}=\sqrt[4\bullet 3]{7}=\sqrt[12]{7}\)
b) \(\sqrt[2]{\sqrt[3]{{{x}^{7}}}}=\sqrt[2\bullet 3]{{{x}^{7}}}=\sqrt[6]{{{x}^{7}}}=\sqrt[6]{{{x}^{6}}\bullet x}=\bullet \sqrt[6]{x}=x\sqrt[6]{x}\)
c) \(\sqrt[4]{x\sqrt{x}}=\sqrt[4]{\sqrt{{{x}^{2}}\bullet x}}=\sqrt[8]{{{x}^{3}}}\)
Obsérvese que en el ejemplo b), se descompuso la potencia de x como producto de dos factores, con la finalidad de simplificar la expresión al máximo. Y en el ejemplo c) se introdujo en la raíz cuadrada el factor “x”, que se encontraba fuera de ella, antes de multiplicar los índices de las respectivas raíces.
4.- Potencia de una raíz
Al elevar una raíz a una determinada potencia, se debe elevar la cantidad subradical a dicha potencia, así:
\({{\left( \sqrt[n]{a} \right)}^{m}}=\sqrt[n]{{{a}^{m}}}\)
Ejemplo
a) \({{\left( \sqrt[3]{{{x}^{2}}} \right)}^{2}}=\sqrt[3]{{{x}^{4}}}=\sqrt[3]{{{x}^{3}}\bullet x}=\sqrt[3]{{{x}^{3}}}\bullet \sqrt[3]{x}=x\bullet \sqrt[3]{x}\)
Ecuaciones con radicales
Se trata de ecuaciones en las cuales la incógnita aparece como cantidad subradical.
Ejemplo a resolver
\(\sqrt{3x+1}=4\)
Se eleva al cuadrado en ambos lados de la ecuación, para eliminar la raíz:
\({{\left( \sqrt{3x+1} \right)}^{2}}={{4}^{2}}\)
\(3x+1=16\)
\(x=\frac{16-1}{3}=\frac{15}{3}=5\)

Trabajo publicado en: Jun., 2021.