Qué es Rectángulo

Ingeniera Industrial, MSc en Física, y EdD
Un rectángulo es una configuración geométrica de propiedad plana cuya forma se caracteriza por tener cuatro ángulos rectos (de 90 grados, que totalizan internamente 360 grados) determinados a partir de sus cuatro lados, donde los respectivos opuestos son paralelos y congruentes entre sí. Es un tipo especial de paralelogramo. Por el latín rectangŭlus, está constituido sobre rectus, de recto, y angŭlus, con base en la forma griega ἀγκύλος (ankýlos), en cuanto adjetivo que describe algo ‘arqueado’, ‘inclinado’, ‘encorvado’. Se distingue como una forma muy común en la geometría y en la vida cotidiana, y se utiliza en la construcción de edificios, la fabricación de mobiliario, en la creación de planos topográficos, etc.
Por ejemplo, la mesa de billar forma un rectángulo, cuyas dimensiones estándar son de 188 cm x 96 cm para el área de juego.
Características y propiedades
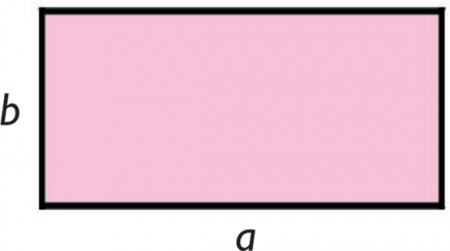 • Tiene cuatro lados que son congruentes dos a dos, es decir, los lados opuestos tienen la misma longitud.
• Tiene cuatro lados que son congruentes dos a dos, es decir, los lados opuestos tienen la misma longitud.
• Tiene cuatro ángulos rectos, lo que significa que cada ángulo mide 90 grados.
• Tiene dos diagonales que son congruentes y se cruzan en el centro del rectángulo.
• Sus lados opuestos son paralelos.
En cuanto a los ejes de simetría, un rectángulo tiene dos ejes de simetría, cada uno de los cuales divide el rectángulo en dos mitades iguales. Los ejes de simetría pasan a través del centro del rectángulo y son perpendiculares entre sí. En un rectángulo, el centro geométrico se encuentra en el punto de intersección de las diagonales.

Los rectángulos son cuadriláteros con cuatro lados congruentes, dos a dos, y cuatro ángulos rectos. Tienen dos ejes de simetría que se cruzan en su centro geométrico. En la sección transversal hueca del bloque se aprecian los ejes de simetría de dicha sección.
¿Cómo se determina la diagonal en un rectángulo?
Para determinar la diagonal de un rectángulo, se puede utilizar el teorema de Pitágoras. El teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los otros dos lados. En el caso del rectángulo, los otros dos lados son la base y la altura.
Por lo tanto, para calcular la diagonal de un rectángulo con base b y altura h, se puede hacer lo siguiente:
Encontrar la longitud de uno de los lados del triángulo rectángulo formado por la diagonal, la base y la altura. En este caso, puede elegir la base o la altura como uno de los lados del triángulo. Por ejemplo, si se elige la altura, la longitud del lado será h.
Encontrar la longitud del otro lado del triángulo rectángulo. En este caso, será la base. Por lo tanto, la longitud del otro lado será b.
Utilizar el teorema de Pitágoras para encontrar la longitud de la hipotenusa, que será la diagonal del rectángulo. Así que, la diagonal (D) se puede calcular como:
\(D = \sqrt {{b^2} + {h^2}} \)
Por ejemplo, si el rectángulo tiene una base de 6 cm y una altura de 8 cm, la diagonal se puede calcular como:
\(D = \sqrt {{6^2} + {8^2}} \)
\(D = \sqrt {36 + 64} = \sqrt {100} = 10\;cm\)
Por lo tanto, la diagonal de este rectángulo es de 10 cm.

A nivel comercial, las dimensiones de un monitor en pulgadas, se refieren a la medida de su diagonal; así, si un televisor tiene 42”, ello implica la medida de su diagonal, trazando una línea que cruza del extremo superior izquierdo (o derecho) al inferior derecho (o izquierdo).
Área y perímetro
Para calcular el área y perímetro de un rectángulo, se puede utilizar las siguientes fórmulas:
Área = base x altura
Perímetro = 2 x (base + altura)
Donde la base y la altura son las longitudes de los lados del rectángulo.
Por ejemplo, supongamos que tenemos un rectángulo con base de 7 cm y altura de 5 cm. Para calcular el área, se hace lo siguiente:
Área = base x altura
Área = 7 cm x 5 cm Área = 35 cm²
Para calcular el perímetro, se hace lo siguiente:
Perímetro = 2 x (base + altura)
Perímetro = 2 x (7 cm + 5 cm)
Perímetro = 2 x 12 cm
Perímetro = 24 cm
Por lo tanto, el área de este rectángulo es de 35 cm² y su perímetro es de 24 cm.
Ejemplos de aplicación práctica

El rectángulo es una de las figuras geométricas más simples y a la vez apreciada por ingenieros y arquitectos, debido a su gran valor estético y simetría.
• Marcos y cuadros: Muchos cuadros y marcos son de forma rectangular, lo que los hace fáciles de enmarcar y colgar en las paredes.
• Pantallas electrónicas y televisores: La mayoría de las pantallas electrónicas, incluyendo los televisores, tienen forma rectangular.
• Construcción: Los ladrillos y bloques utilizados en la construcción son en su mayoría rectangulares, lo que facilita enormemente el proceso de construcción.
• Ventanas y puertas: Muchas ventanas y puertas tienen forma rectangular, lo que permite que encajen adecuadamente en las aperturas de las paredes.
• Cajas y paquetes: Muchas cajas y paquetes vienen en forma rectangular o cuadrada, lo que los hace fáciles de apilar y transportar.
• Terrenos y lotes: Las propiedades en forma de rectángulo son muy comunes en la planificación urbana y en la subdivisión de terrenos.
• Libros y cuadernos: La mayoría de los libros y cuadernos tienen una forma rectangular, lo que los hace fáciles de apilar y almacenar.

Art. actualizado: Abril 2023; sobre el original de noviembre, 2012.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.