Significado de red neuronal artificial Definición, perceptrón, y procesos

Doctor en Ingeniería
Definición formal
La red neuronal artificial es una combinación de funciones lineales y no lineales que se utilizan para aproximar funciones de muy alta complejidad en el marco de las ciencias de la computación.
Estas redes se componen de perceptrones (o nodos), que son funciones que buscan imitar el comportamiento de las neuronas en el cerebro humano, y es lo que le da origen al término.
Dada su estructura, las Redes Neuronales tienen la capacidad de «aprender» de los datos y son muy utilizadas para resolver problemas de Clasificación, Visión Computacional, Generación de Datos Artificiales, Reconocimiento de Habla y Predicción.
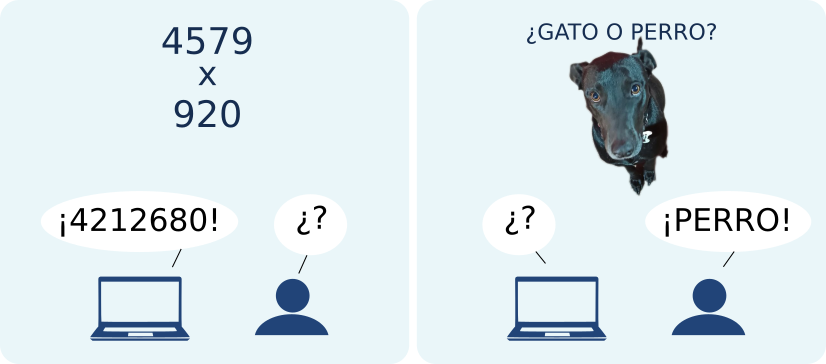
La ventaja de este tipo de modelos con respecto a aquellos modelos matemáticos más básicos radica en que la capacidad de aprendizaje permite resolver tareas muy complejas desde el punto de vista computacional aunque a veces sencillas para las personas. En otras palabras, queríamos una manera de identificar un animal en una foto, y puesto que es muy difícil construir una función que lo haga, pero es muy sencillo para el cerebro humano, entonces construimos una función que imite el cerebro e hicimos que aprenda la tarea.
¿Cómo funcionan las Redes Neuronales?: Perceptrón
Si bien hay muchos tipos de estructuras posibles de Redes Neuronales que pueden utilizarse según la tarea a resolver, la primera e inspirada en las neuronas del cerebro se denomina Perceptrón Multicapa. Una neurona biológica emite o no una respuesta en forma de impulso eléctrico dependiendo de los estímulos percibidos, que pueden a su vez ser generados por otras neuronas.
La idea consiste en imitar este comportamiento mediante una función lineal que «percibe» los estímulos y una función de activación no-lineal que dispara (o no) la señal de salida.
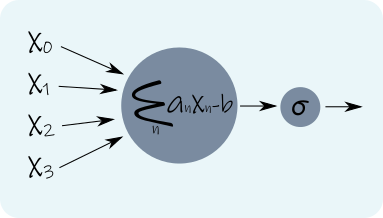
La formulación matemática del perceptrón es la siguiente:
\(y = \sigma\left(\sum_n a_n x_n -b\right)\)
donde xn son las entradas que recibe el perceptrón, an son los pesos de la combinación lineal, b es un parámetro interno que se conoce como bias y Σ es la función de activación, típicamente una sigmoidea, definida como
\(\sigma(x) = \frac{1}{1+e^{-x}}\)
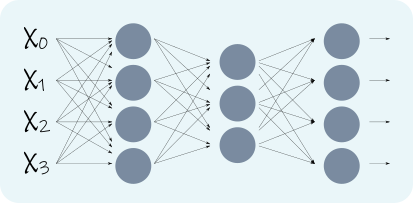
Por sí mismo, el perceptrón no parece demasiado espectacular, pero su enorme capacidad se desplega cuando se unen varios perceptrones, formando una \emph{Red Neuronal}, como se ve en la Figura \ref{fig:mlp}, que para una red de tres capas tiene la forma
\(y = \sigma\left(\sum_n a^{(3)}_{n,m}\left(\sum_m\sigma\left(\sum_n a^{(2)}_{n,m}\left(\sum_m\sigma\left(\sum_n a^{(1)}_{n,m} x_n -b^{(1)}_{m}\right)\right)-b^{(2)}_{m}\right)\right)-b^{(3)}_{m}\right)\)
donde n es el índice de la entrada, m el número de neurona y el superíndice entre paréntesis indica el número de capa. Esta expresión es mucho más complicada que la anterior, y sin analizarla en profundidad puede verse que la red cuenta con una gran cantidad de parámetros: en cada capa tenemos \(M\times(N+1)\) parámetros, donde N es la cantidad de entradas y M el número de neuronas en la capa. Esto le da una gran capacidad a la Red de aproximar funciones y resolver tareas complicadas.
Procesos de entrenamiento
Ya hemos visto que un Perceptrón Multicapa tiene una enorme capacidad, permitiendo aproximar funciones muy intrincadas a través de su gran cantidad de parámetros. No obstante, ¿de dónde sacamos los valores para esos parámetros? El secreto de todo esto es hacer que la Red aprenda los parámetros. La manera más común de hacer esto es mediante ejemplos etiquetados de entrenamiento.
Supongamos que queremos entrenar un clasificador que sepa distinguir gatos de perros. Entonces, la idea es mostrarle (darle como entrada) a la red una imagen de -digamos- un perro. Si la salida de la red y = «perro», entonces todo está bien. Si, en cambio, y = «gato», entonces cambiamos ligeramente los parámetros de la red tratando de que ese ejemplo sea clasificado como «gato». Esto se hace mediante un proceso conocido como backpropagation, que no es otra cosa que un descenso por gradiente. La idea es continuar mostrando ejemplos y corrigiendo la salida de la red haciendo que se equivoque cada vez menos, y finalmente aprenda la tarea.
Para tareas que involucran procesamiento de imágenes (como la clasificación gato/perro) existen otro tipo de redes con mejor desempeño llamadas «convolucionales», cuya idea de funcionamiento es la misma. A otras tareas conviene atacarlas mediante redes definidas en grafos, redes de Aprendizaje por Refuerzo, Autoencoders o Redes Adversarias. No se pueden nombrar todas, y día a día aparecen nuevos modelos con capacidades propias.

Trabajo publicado en: Ene., 2021.