Significado de las reglas de Kirchhoff Definición, procedimiento, y ejemplos

Licenciada en Física
Definición formal
Las leyes de Kirchhoff o más bien las reglas, pues no son leyes en el sentido estricto, consisten en la aplicación a los circuitos eléctricos de dos principios fundamentales de la Física: la conservación de la carga eléctrica y la conservación de la energía.
Resultan muy útiles cuando se trata de circuitos resistivos que no se reducen a combinaciones de resistencias en serie y paralelo.
La primera regla establece que la suma algebraica de las corrientes en cualquier nodo o unión del circuito es 0:
∑ I = 0
Equivale a la aplicación del principio de conservación de la carga eléctrica e indica que la suma de todas las corrientes que entran a una unión o nodo, debe resultar igual a la sumatoria de las que salen del mismo. Esto implica que la carga no se acumula en un nodo, sino que fluye continuamente por todo el circuito.
La segunda regla afirma que la suma algebraica de los voltajes en cualquier porción cerrada de circuito o malla es 0:
∑ ε = 0
Esta es otra manera de expresar la conservación de la energía, ya que, partiendo de cualquier punto de la malla, la energía por unidad de carga que provee la fuerza electromotriz (abreviada como fem) es igual a la que se pierde luego de recorrer la malla y volver al punto de partida.
La energía se puede obtener a través de las reacciones químicas de la batería, pero a medida que la corriente circula por el circuito, se pierde al pasar por una resistencia o cuando hace algún tipo de trabajo, como poner en marcha un motor.
Procedimiento
Paso 1: Se comienza asignando un sentido a la corriente que pasa por cada rama y dibujándolo en el esquema correspondiente, en caso de que el circuito no lo indique en los datos iniciales suministrados. No importa que el sentido asignado a la corriente sea diferente al verdadero, ya que, al resolver el sistema de ecuaciones resultante, este se pondrá en evidencia de inmediato.
Paso 2: Enseguida, se escoge un nodo para plantear la primera regla de Kirchhoff. Para ello hay que asignarle uno de los signos a las corrientes que entran al nodo, y otro a las que salen de él y la suma algebraica debe ser 0.
Paso 3: Después se selecciona una malla para aplicar la segunda regla. Como se dijo anteriormente, una malla es una porción cerrada de circuito. Se escoge un punto cualquiera de ella como inicio del recorrido para sumar los voltajes, que incluyen el de cada pila que se encuentre en el camino, así como de las caídas o subidas de potencial al pasar por cada resistencia.
A cada uno de estos elementos se le coloca un signo de acuerdo a la convención.
Signos para las baterías
– Cuando se recorre una fuente en el sentido de − a +, se considera una subida de potencial y se le asigna signo +.
– Si el sentido de la fuente es de + a −, es una caída de potencial y lleva signo −.
Signos para las resistencias
– Al pasar por la resistencia en el mismo sentido de la corriente asignada, es una caída de potencial y lleva signo −.
– Si se pasa por la resistencia en sentido contrario al de la corriente asignada, se considera subida de potencial y lleva signo +.
El voltaje V de cada resistencia se calcula a través de la ley de Ohm:
V = I∙R
Donde I es la corriente pasa por la resistencia R.
Siguiendo este procedimiento para cada malla, se construyen ecuaciones donde las incógnitas pueden ser las corrientes, los voltajes o las resistencias, según los datos que se conozcan previamente del circuito. Se requiere por lo menos de igual número de ecuaciones que de incógnitas para encontrar la solución.
Paso 4: El sistema de ecuaciones resultante se resuelve con alguno de los muchos métodos que existen para ello.
Ejemplos de aplicación
Aplicando las reglas de Kirchhoff, hallar la corriente y el voltaje a través de cada resistencia en el circuito mostrado a continuación:
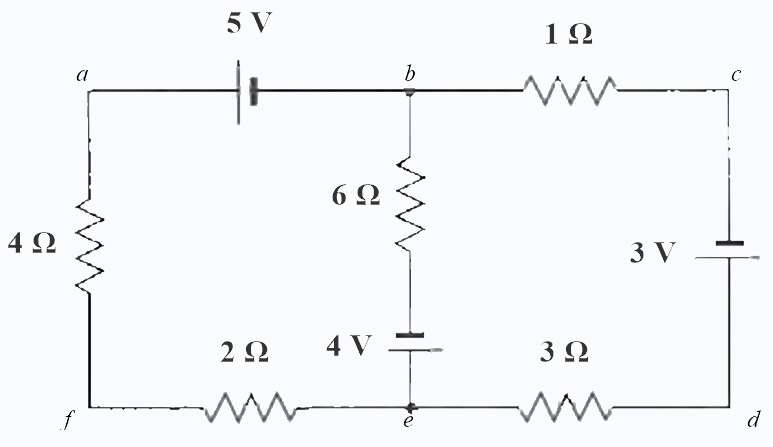
Respuesta
Primero se asigna un sentido arbitrario a las corrientes:
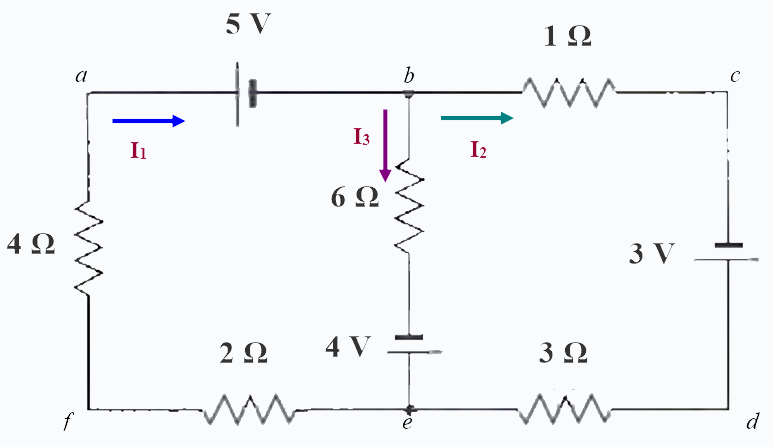
Y seguidamente se plantea la primera regla de Kirchhoff mediante el nodo b (el node e también se puede usar), esto proporciona la primera ecuación. Las corrientes que entran son positivas y las que salen negativas. En este caso entra solamente la corriente I1 y salen las corrientes I2 e I3, por lo tanto:
Ecuación 1: I1 – I2 – I3 = 0
La segunda ecuación proviene de aplicar la segunda regla de Kirchhoff a alguna de las mallas, por ejemplo la malla abefa.
Comenzando en el punto a, lo primero que se encuentra es la batería de 5 V, la cual va de + a −, enseguida se aplica la ley de Ohm con la corriente I3 a la resistencia de 6 Ω, luego está la batería de 4 V de − a +, siguen las resistencias de 2Ω y 4 Ω por las que pasa la corriente I1. La ecuación resultante es:
−5 − 6I3 + 4 − 2I1 − 4I1 = 0
Ecuación 2: − 6I1 − 6I3 = 1
De la malla bcdeb se obtiene una tercera ecuación:
− I2 + 3 − 3I2 − 4 + 6I3 = 0
Ecuación 3: − 4I2 + 6I3 = 1
Como hay tres incógnitas I1, I2 e I3, es suficiente con tres ecuaciones. La solución del sistema es:
I1 = − 0.19 A; I2 = − 0.21 A; I3 = 0.024 A.
El significado del signo negativo que precede a I1 e I2 es muy simple: estas corrientes circulan en sentido opuesto al asignado originalmente. Se deja como ejercicio para el lector encontrar los voltajes en cada resistencia mediante la ecuación V = I∙R.

Trabajo publicado en: Feb., 2021.