Definición de Distribución y Regresión de Poisson

Marcoantonio Villanueva Bustamante
Doctor en Psicología

La regresión de Poisson es una técnica de análisis de regresión que se emplea cuando la variable que se intenta predecir posee una distribución de Poisson, en cuyo caso implica una distribución de probabilidad discreta que se expresa a partir de la probabilidad de la ocurrencia de un determinado número de eventos en un periodo de tiempo determinado.

En las ciencias sociales, al igual que el resto de las ciencias, se tiene como objetivo el tratar de explicar la ocurrencia de sus fenómenos de estudio. Sin embargo, las ciencias sociales tienen el problema de que los fenómenos que estudian están expuestos a demasiadas variables extrañas, por lo que no es posible emplear modelos algebraicos para predecir la ocurrencia de fenómenos; por el contrario, se emplean modelos estadísticos y de probabilidad. Uno de estos modelos es el Análisis de Regresión¸ el cual intenta predecir los valores que presentará una variable en función de otra. Es así que es posible categorizar estos modelos de regresión en diferentes tipos de regresión. La primera categoría es el análisis de regresión lineal, que involucra la relación entre dos variables cuantitativas (intervalares o de razón); el segundo tipo de regresión involucra la relación de variables cuantitativas con variables categóricas (regresión logística); un tercer tipo de regresión es aquella que aborda la relación de una variable continua con una variable que presentan una distribución no continua, por ejemplo, una distribución binomial o de Poisson.

La regresión de Poisson es una técnica de análisis de regresión que se emplea cuando la variable que se intenta predecir posee una distribución de Poisson. Sin embargo, previo a comprender el concepto de regresión de Poisson es necesario comprender los conceptos de distribución binomial y distribución de Poisson.

Distribución binomial

Cuando se realiza un experimento o un ensayo puede suceder que tenga únicamente dos resultados que son exclusivos de manera simultánea, es decir, solo puede ser uno u otro. (por ejemplo, al lanzar una moneda solamente se puede obtener cara o cruz; al responder a una pregunta de una prueba de rendimiento se obtendrá una respuesta correcta o incorrecta). De este modo, adquiere el nombre de ensayo de Bernoulli y emplea la terminología éxito-fracaso o ausencia-presencia. Pues bien, la distribución binomial se emplea para conocer cual es la probabilidad asociada al numero de éxitos (o fracasos) de un conjunto de ensayos de Bernoulli. Dicho de otra manera, indicaría cuantos éxitos o fracasos se obtendrían de un numero determinado de ensayos. Como puede inferirse, la distribución binomial permite trabajar con variables dicotómicas, sin embargo, a diferencia de otras técnicas de análisis, este tipo de distribución solo se trabaja con solo uno de los valores (n1 = éxitos o n0 = fracasos). La expresión matemática que se emplea para describir esta distribución es la siguiente:

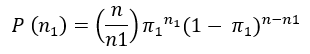
Distribución de Poisson

La distribución de Poisson es básicamente lo mismo que la distribución binomial, es decir, es una distribución de probabilidad discreta que se expresa a partir de la probabilidad de la ocurrencia de un determinado número de eventos en un periodo de tiempo determinado.

De este modo, la diferencia entre la distribución binomial y la Poisson es que la primera evalúa la probabilidad en un determinado número de ensayos mientras la segunda lo hace en un determinado lapso de tiempo.

Regresión de Poisson

La regresión de Poisson es un tipo de regresión que se emplea para analizar un tipo particular de respuestas dicotómicas llamadas recuentos. El concepto de recuento se refiere al número de ocurrencias de un evento en un periodo de tiempo determinado. En este sentido, no se debe confundir el concepto de recuento con el de frecuencia; debido a que este último se emplea para describir el patrón de variabilidad de las respuestas, mientras que el primero refleja cuantas veces se presenta una respuesta.

Los recuentos siempre serán valores enteros no negativos con una distribución que típicamente presenta una asimetría positiva; si bien es posible establecer un modelo de regresión para los recuentos con un modelo lineal, la realidad es que el modelo más adecuado es el modelo de regresión de Poisson, la cual se expresa con la siguiente formula:

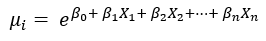
Este modelo modifica ligeramente la formula clásica de la regresión lineal, esto al cambiar el predictor lineal como una potencia e, que es la base del logaritmo natural, evitando así la posibilidad de contar con un pronostico negativo. Dicho de otro modo, al tomar el pronóstico que se obtiene en el modelo lineal y se eleva mediante un logaritmo natural se obtendrá un valor positivo para \mu_i. Por otro lado, este modelo tiene la “ventaja” que no requiere que se cumpla el supuesto de normalidad; tampoco requiere que las varianzas sean homogéneas.

En síntesis, si bien la regresión lineal podría pronosticas los valores de un recuento, su rigidez en cuanto a los supuestos y la lógica matemática que posee no permitiría realizar inferencias libres de sesgos o errores de interpretación; por lo que la regresión de Poisson es una mejor alternativa.

Por: Marcoantonio Villanueva Bustamante. Licenciado en Psicología, egresado de la Facultad de Psicología de la UNAM, México. Doctor en Psicología por la UFRO, Chile. Actualmente, es investigador independiente que forma parte de diversos equipos de investigación en México y Chile.

Trabajo publicado en: Jun., 2024.

Datos para citar en modelo APA: Villanueva Bustamante, M. (junio, 2024). Definición de Distribución y Regresión de Poisson. Significado.com. Desde https://significado.com/regresion-poisson/