Definición de Rombo
Ingeniera Industrial, MSc en Física, y EdD
El rombo es una forma geométrica plana que debe ser descrito como un cuadrilátero (es decir, una figura que contiene cuatro lados) - paralelogramo (es decir, que hay dos pares de lados paralelos entre sí). El rombo puede ser visto como un cuadrado o un rectángulo apenas inclinado. El nombre que recibe esta forma geométrica tiene que ver con el idioma griego para el cual el término ῥόμβος (rómbos) hace referencia a aquellas formas que giran interminablemente.
Tal como sucede con otros cuadriláteros, el rombo se compone de cuatro lados cerrados que forman su perímetro. Estos cuatro lados son siempre equivalentes en longitud entre sí, ya que si alguno de ellos presentara una mínima diferencia con otros estaríamos hablando de un romboide y no de un rombo. Estos cuatro lados forman dos ejes internos o diagonales que tocan los vértices en los cuales dos lados se unen y que son perpendiculares. Los cuatro vértices y/o ángulos internos de un rombo no son de noventa grados, ya que las rectas están inclinadas y no son perpendiculares entre sí.
Presencia de paralelismo en la construcción
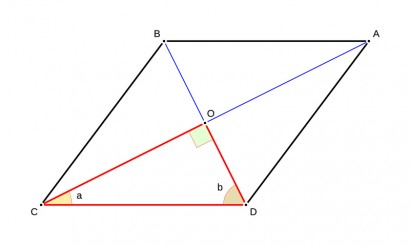Otro de los elementos importantes que caracterizan a los rombos es la existencia de paralelismo entre sus dos pares de lados. Así, los dos lados que se oponen son paralelos entre sí aunque la distancia entre ellos puede variar dependiendo del tipo de rombo que sea. Los rombos son junto a los cuadrados y a los triángulos una de las formas geométricas más comunes y simples de analizar ya que todos sus lados son equivalentes entre sí y, por tanto, la suma de sus ángulos y la manera de establecer las diagonales es siempre igual.
La siguiente imagen muestra un patrón que parecen cubos, sin embargo, las caras o vistas de los cubos son realmente rombos, que en el arreglo se perciben como figuras tridimensionales.
En algunos contextos, como en el ámbito de la seguridad industrial, también se puede referir al rombo como un símbolo para indicar el nivel de riesgo de una sustancia. Asimismo, hay un instrumento musical llamado rombo que consiste en una pieza pequeña de madera o hueso con una cuerda atada.
Resumen de las Características de los rombos
• Es un paralelogramo con los cuatro lados iguales
• Sus ángulos opuestos son iguales
• Tiene un par de ángulos agudos y otro par de ángulos obtusos
• Las diagonales perpendiculares bisecan a cada una, dividiendo al rombo en cuatro triángulos congruentes.
• La suma de las medidas de sus ángulos interiores es igual a 360 grados.
De manera simplificada, el contorno de un diamante se suele representar como un rombo. Tal es el caso de la carta de “diamante”, cuyo símbolo es en realidad un rombo.
¿Cómo se dibuja un rombo?
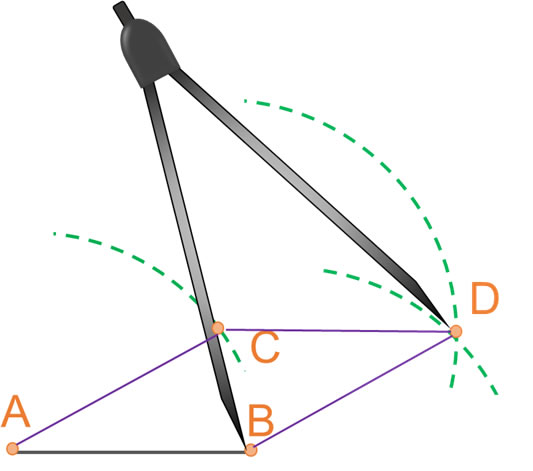
Para construir esta figura se pueden utilizar diferentes métodos. Acá se describe la técnica que requiere el uso compás y regla y se debe conocer la longitud de sus lados:
• Dibujar una recta y marcar dos puntos A y B separados a una distancia equivalente a la medida de los lados del rombo.
• Colocar la punta del compás en el punto A del segmento (hacer centro en A), y con abertura tal que la otra punta llegue al otro extremo B (abertura AB).
• Con esta abertura, trazar desde A un arco en la parte superior del segmento AB.
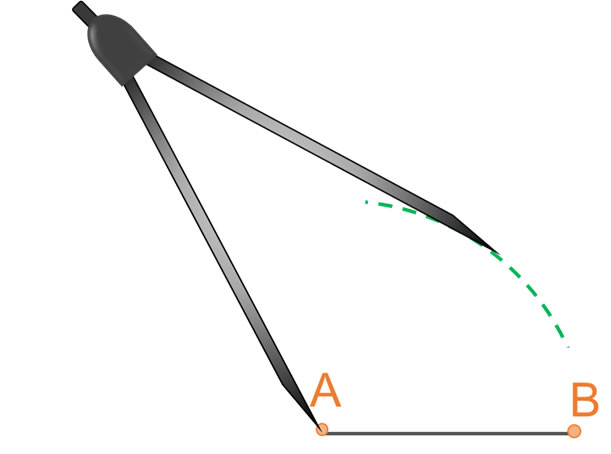
• Haciendo con el compás centro en un punto arbitrario del arco dibujado, que llamaremos C, se traza otro arco en la parte superior (conservando la misma abertura AB del compás).
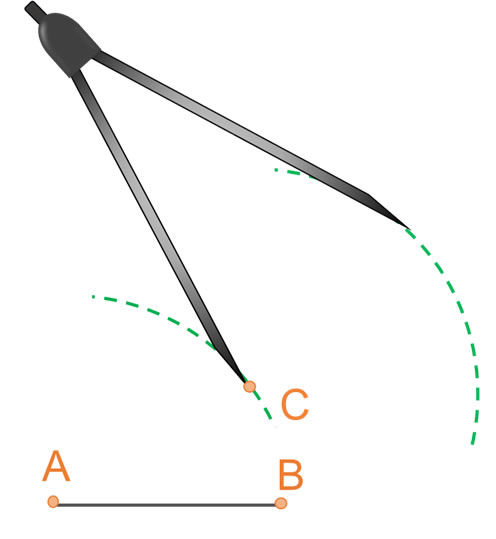
• Haciendo centro ahora en B, y con abertura AB, se traza un arco que intersecte al arco dibujado en el paso anterior. El punto de intersección será D.
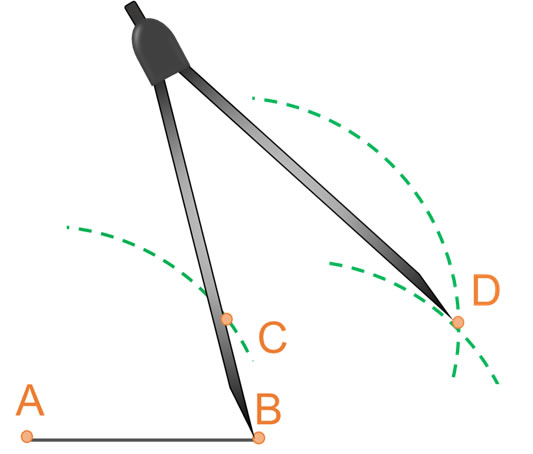
• Finalmente, los puntos A, B, C y D, son los vértices del rombo, por lo que se procede a unir con una recta los punto B y D; D con C y C con A.
Área y perímetro
Al igual que cualquier paralelogramo, el área (A) de un rombo se determina multiplicando la medida de su base (b) por su altura (h):
A = b x h
Puesto que b y h tienen dimensiones de longitud, el área se expresaría en unidades de longitud al cuadrado, por ejemplo, centímetros cuadrados (cm2).
Sin embargo, en ocasiones, solo se conocen las diagonales del rombo, en cuyo caso, el área se determina mediante la expresión:
\({A_{rombo}} = \frac{{D \times d}}{d}\)
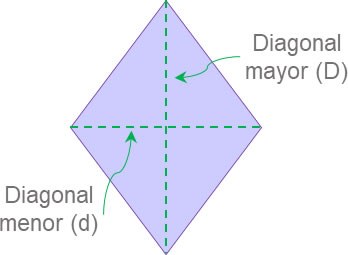
Donde D y d son las diagonales mayor y menor del rombo, respectivamente.
En lo que respecta al perímetro (P), este se obtiene mediante la suma de todos sus lados; es decir, si se denomina “a” a la longitud de cada lado de la figura, su perímetro (P) es:
P = 4a
En caso de que se conozcan las dimensiones de las diagonales del rombo (d y D), es necesario aplicar el teorema de Pitágoras para calcular la medida de sus lados, y luego este valor se multiplica por 4 para obtener el perímetro:
\(a = \sqrt {{{\left( {\frac{D}{2}} \right)}^2} + {{\left( {\frac{d}{2}} \right)}^2}} = \sqrt {\frac{{{D^2}}}{4} + \frac{{{d^2}}}{4}} = \frac{{\sqrt {{D^2} + {d^2}} }}{2}\)
El perímetro resulta:
Ejemplo: Se tiene una parcela como la mostrada en la imagen, y se desea determinar su perímetro para colocarle una cerca alrededor de todo el contorno. Se sabe que las diagonales miden 30 metros y 40 metros. ¿Qué longitud debe tener la cerca perimetral a instalar?
Solución: Debido a que se conocen las diagonales del rombo, solo se debe determinar el perímetro aplicando la fórmula anterior, y con ello se obtendrá la longitud que deberá tener la cerca:
\(P = 2\sqrt {{D^2} + {d^2}} = 2\sqrt {{{30}^2} + {{40}^2}} = 100\;m\)
Se requieren como mínimo, 100 m de cerca.
Los romboides
Se trata de una figura geométrica plana que pertenece al grupo de los paralelogramos, con la particularidad que posee lados opuestos iguales y paralelos, es decir, tiene dos medidas diferentes de lados. Al igual que el rombo, cuenta con un par de ángulos agudos y otro par de ángulos obtusos.
Las torres inclinadas KIO tienen una altura de 114 metros y se encuentran ubicadas en la Plaza de Castillas, Madrid. Una de sus características distintivas es que sus caras laterales son de forma romboidal.
Art. actualizado: Marzo 2023; sobre el original de agosto, 2010.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.