Definición de Perímetro (en Matemáticas, Geometría)

Licenciado en Física
El perímetro es la longitud de la frontera o contorno que delimita a una región o superficie cerrada en un espacio de dos dimensiones. Mientras que el área mide la extensión de una superficie, el perímetro es una medida del contorno de esta.
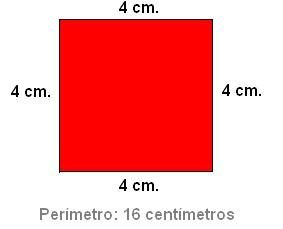 El término de perímetro aparece en diversos contextos y disciplinas. Por ejemplo, si queremos cercar un terreno tenemos que conocer el perímetro de este para poder saber cuánto alambrado necesitamos. Podemos calcular la distancia recorrida por un auto de carreras al completar una vuelta de un circuito si conocemos el perímetro de la pista. En esta ocasión abordaremos el tema de perímetro desde las matemáticas y la geometría.
El término de perímetro aparece en diversos contextos y disciplinas. Por ejemplo, si queremos cercar un terreno tenemos que conocer el perímetro de este para poder saber cuánto alambrado necesitamos. Podemos calcular la distancia recorrida por un auto de carreras al completar una vuelta de un circuito si conocemos el perímetro de la pista. En esta ocasión abordaremos el tema de perímetro desde las matemáticas y la geometría.
¿Cómo se calcula el perímetro de una figura?
Supongamos que tenemos un polígono que tiene \(n\) lados, cada lado lo identificamos con la letra \(l\) y un subíndice \(i\) que indica el número de lado, este subíndice va de \(1\) a \(n\), de tal manera que el lado 3 será \({l_3}\).
Todos estos lados determinan el contorno de la figura. El perímetro, al ser la longitud del contorno de la figura, será simplemente la suma de las medidas de todos los lados que conforman la figura. Sea \(P\) el perímetro, podemos decir entonces que:
\(P = \mathop \sum \limits_{i = 1}^n {l_i} = {l_1} + {l_2} + \ldots + {l_n}\)
El cálculo del perímetro de una figura consiste básicamente en sumar las medidas de los lados que la componen. Esto claramente tiene sus excepciones como es el caso del círculo, que no tiene lados como otras figuras y que el cálculo de su perímetro de diferente.
Perímetros de algunas figuras geométricas
A continuación, se mostrará cómo calcular el perímetro de algunas figuras geométricas comunes que se utilizan con regularidad.
Cuadrado
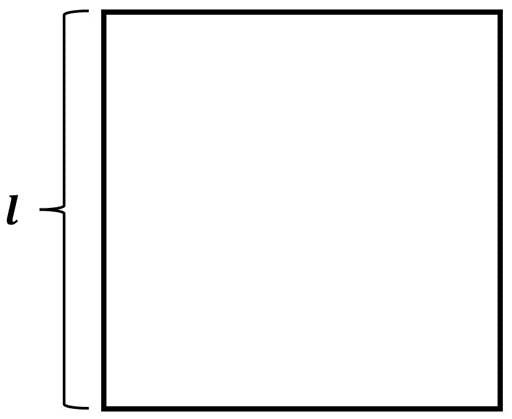
Los cuatro lados que componen un cuadrado son iguales entre sí. Suponiendo que se tiene un cuadrado de lado \(l\), su perímetro será:
\(P = l + l + l + l\)
Lo cual nos da como resultado:
\(P = 4l\)
Rectángulo
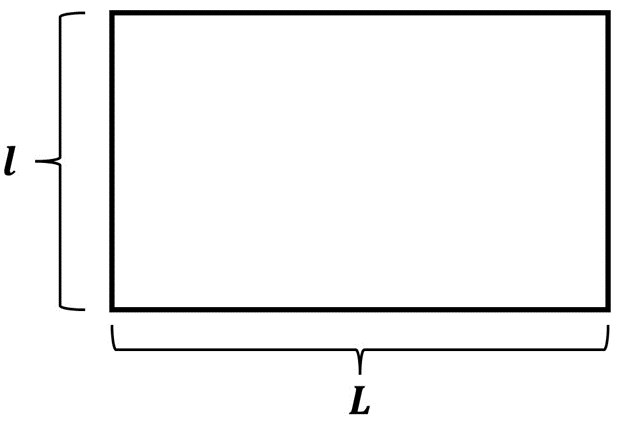
Un rectángulo es un paralelogramo con un par de lados \(L\) que son iguales entre sí y otro par de lados \(l\) que también son iguales, todos los lados forman ángulos rectos entre sí. Considerando este mismo caso, el perímetro de un rectángulo estará dado por:
\(P = L + L + l + l\)
Sumando términos semejantes tenemos que:
\(P = 2L + 2l\)
Lo cual factorizando queda finalmente como:
\(P = 2\left( {L + l} \right)\)
Nótese que el cuadrado es un caso especial que ocurre cuando \(L = l\)
Triángulo
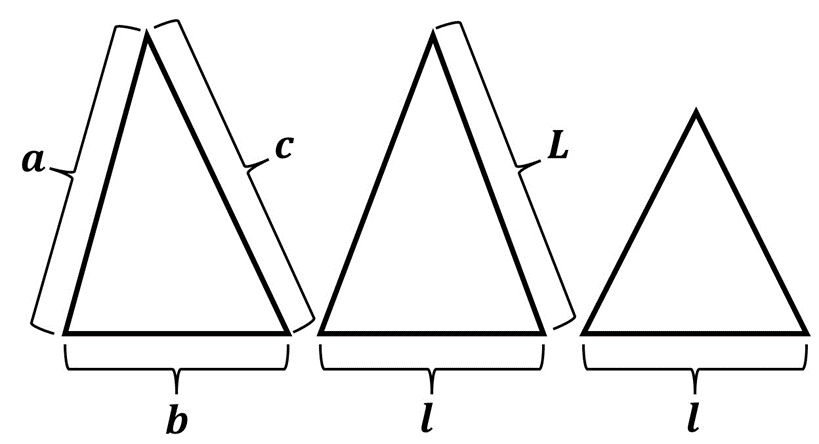
Un triángulo es una figura geométrica formada por tres lados. Existen distintos tipos de triángulos dependiendo de las medidas de sus lados. Consideremos primero un triángulo escaleno, este es un tipo de triángulo en el que sus tres lados son diferentes entre sí. Sean \(a\), \(b\) y \(c\) los lados del triángulo escaleno, el perímetro de este será:
\(P = a + b + c\)
Imaginemos que ahora tenemos un triángulo isósceles, este es un tipo de triángulo que tiene dos de sus lados iguales. Si los lados iguales entre sí son \(L\) y el lado es \(l\), entonces el perímetro de este triángulo isósceles estará dado por:
\(P = L + L + l\)
Lo cual simplificando nos lleva a:
\(P = 2L + l\)
Finalmente, supongamos que tenemos un triángulo equilátero. Este tipo de triángulo se caracteriza por tener sus tres lados iguales. Sea \(l\) la medida de los lados de un triángulo equilátero, su perímetro lo podemos calcular de la siguiente manera:
\(P = l + l + l\)
Lo cual sencillamente se resume a:
\(P = 3l\)
Rombo
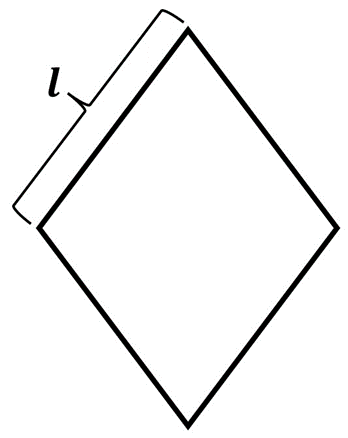
Un rombo es un paralelogramo formado cuatro lados iguales. Se diferencia esta figura del cuadrado debido a que, a diferencia de este, los lados de un rombo no forman ángulos rectos entre sí. Si se tiene un rombo cuyos lados miden \(l\), el perímetro de este será:
\(P = l + l + l + l\)
Agrupando todos los términos obtenemos que:
\(P = 4l\)
Polígono regular
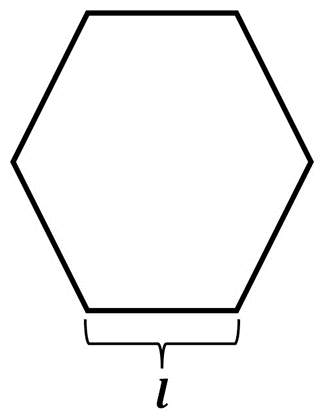
Un polígono regular es una figura geométrica que se compone de lados y ángulos interiores que son iguales entre sí. El triángulo equilátero y el cuadrado son ejemplos de polígonos regulares, al igual que el pentágono y el hexágono. De manera general podemos considerar un polígono regular con \(n\) lados que miden \(l\) cada uno. El perímetro de este polígono regular puede expresarse como:
\(P = \mathop \sum \limits_{i = 1}^n l\)
Lo cual nos da como resultado:
\(P = nl\)
Círculo
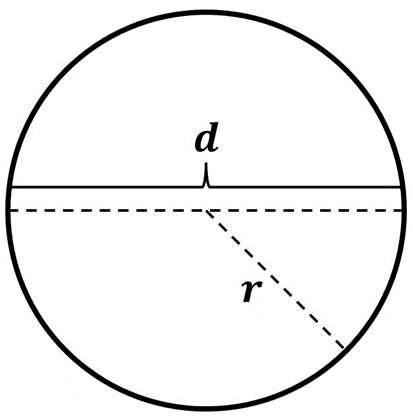
En todos los casos anteriores hemos calculado el perímetro de distintas figuras geométricas simplemente sumando las medidas de sus lados. Esto no ocurre con el círculo, ya que su circunferencia se calcula de distinta manera. La distancia que existe entre el centro del círculo y cualquier punto de su circunferencia se llama “radio”. El perímetro de un círculo de radio \(r\) está dado por:
\(P = 2\pi r\)
Generalmente, el perímetro de un círculo se expresa en términos de su diámetro \(d\), lo cual es una línea que une dos puntos opuestos de la circunferencia y que pasa por su centro. La medida del diámetro es dos veces el radio, es decir que \(d = 2r\). Por lo tanto, la expresión anterior para el perímetro del círculo la podemos escribir en términos del diámetro \(d\) como:
\(P = \pi d\)
De hecho, de aquí es de donde sale la definición del número \(\pi \), ya que:
\(\pi = \frac{P}{d}\)
El número \(\pi \) es el número de veces que cabe el diámetro de una circunferencia en su perímetro y esto es válido para todos los círculos.

Art. actualizado: Oct. 2023; sobre el original de noviembre, 2009.
Referencias
Ronald S. Irving. (2004). Integers, Polynomials and Rings. New York: Springer.H. Behnke, F. Bachmann, K. Fladt, W. Süss, H. Gerike, F. Hohenberg, G. Pickert, H. Rau & S. H. Gould. (1983). Fundamentals of Mathematics: Volume II. Cambridge, Massachusetts and London: The MIT Press.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.