Significado de cuadrado (perímetro, Área, diagonales…) Definición, y ejercicios

Licenciada en Física
Definición formal
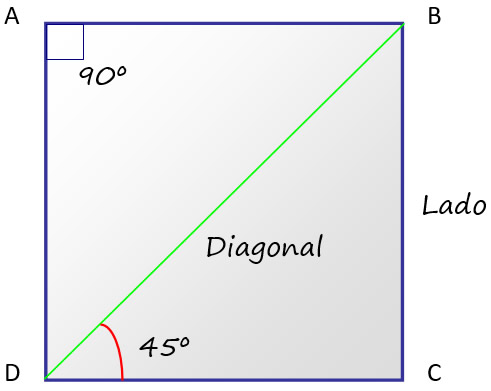
El cuadrado es una figura cerrada y congruente constituida por cuatro lados y los correspondientes ángulos internos, perteneciente a la familia de polígonos cuadriláteros. Los ángulos internos del cuadrado miden 90º cada uno (su suma totaliza 360º), tienen dos pares de lados paralelos y dos diagonales, que unen los vértices opuestos, así mismo son perpendiculares entre sí, y tienen la misma longitud.
En la figura que acompaña estás líneas se muestran los detalles de la estructura geométrica. Obsérvese que la diagonal es bisectriz del ángulo recto, dividiéndolo en dos ángulos de 45º cada uno.
Se lo percibe como uno de los instrumentos geométricos más utilizadas en diseño, produciendo en el espectador una sensación de durabilidad, confianza y estabilidad. Ventanas, baldosas y trazado de calles son apenas algunos aspectos en el ámbito arquitectónico, apenas poniendo algo de atención se los encuentra en multitud de lugares. Muchas ciudades famosas y monumentos de la antigüedad se extienden sobre una superficie cuadrada, por ejemplo, la base de la Gran Pirámide de Giza en Egipto es un cuadrado cuyo lado mide 230.33 m de largo. Pero sin necesidad de ir tan lejos, también se lo identifica en los tableros del ajedrez, las damas, y en los dados.
Perímetro y área del cuadrado: operaciones de cálculo
Entre los cálculos más frecuentes en relación al cuadrado están el perímetro y el área. El perímetro es el contorno de la figura y se determina sumando la longitud de todos los lados. El resultado depende de la longitud del lado.
Si se tiene un cuadrado de lado “a”, el perímetro P es simplemente:
1) P = a + a + a + a = 4a
Por ejemplo, el perímetro de la Gran Pirámide de Giza, cuyo lado es a = 230.33 m es:
P = 4×230.33 m = 921.32 m
En cuanto al área A de un cuadrado, también es muy sencillo calcularla, ya que depende enteramente de la longitud del lado:
2) A = a2
Siguiendo con el ejemplo de la base cuadrada de la Gran Pirámide de Giza, si se desea calcular su área se obtiene:
A = (230.33 m)2 = 53052 m2
Diagonales del cuadrado
La figura tiene dos diagonales mutuamente perpendiculares, es decir, forman 90º entre sí y se cruzan justo en el centro del cuadrado, que es el baricentro de la figura.
Se lo puede dividir en un par de triángulos rectángulos, tomando uno de estos, la diagonal “D” corresponde a la hipotenusa, mientras que los catetos son los lados “a” del cuadrado:
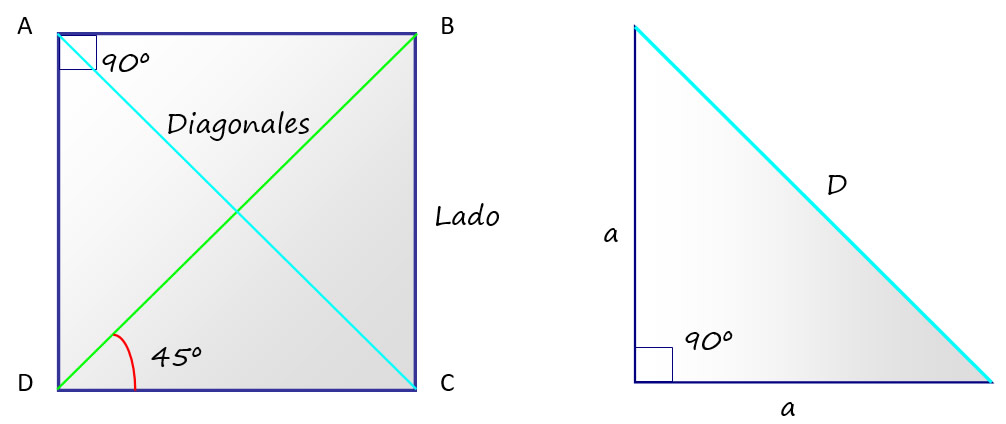
Por lo tanto:
\({{D}^{2}}={{\text{a}}^{\text{2}}}+{{\text{a}}^{\text{2}}}=2{{\text{a}}^{\text{2}}}\)
3) \(D=\sqrt{\text{2}}\cdot a\)
De acuerdo a esto, ¿cuánto mide de esquina a esquina la base de la Gran Pirámide de Giza? Este es precisamente el valor de su diagonal:
\(D=\sqrt{\text{2}}\cdot a=\sqrt{\text{2}}\cdot 230.33\text{ m}=\text{ 325}\text{.74 m}\)
Ejercicios de aplicación
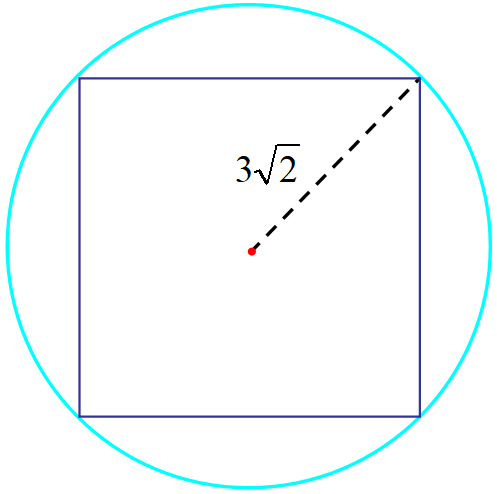
Ejercicio 1: En la siguiente figura hay un cuadrado inscrito en una circunferencia, cuya diagonal partida entre 2 es \(\text{3}\sqrt{2}\), medida en unidades arbitrarias. Responder:
A) ¿Cuál es el diámetro de la circunferencia?
B) ¿Cuánto mide el lado del cuadrado?
C) ¿Qué valor tienen el perímetro y el área del cuadrado?
Respuestas
A) Como el cuadrado está inscrito en toda la circunferencia, sus vértices forman parte de la misma y el centro de ambas figuras geométricas es coincidente. La mitad de la diagonal del cuadrado es el radio de la circunferencia, luego el diámetro es el doble del radio, o si se prefiere, la diagonal completa del cuadrado:
\(\text{D }=\text{ 2}\times \text{3}\sqrt{\text{2}}=6\sqrt{2}\)
B) Para calcular el lado del cuadrado, conociendo la diagonal del mismo, se utiliza la fórmula 3)
\(D=\sqrt{\text{2}}\cdot a\)
Despejando el lado “a” resulta:
\(\text{a}=\frac{\text{D}}{\sqrt{\text{2}}}=\frac{6\sqrt{2}}{\sqrt{\text{2}}}=\text{6}\)
C) El perímetro y el área del cuadrado se calculan mediante las fórmulas 1) y 2) respectivamente:
1) P = 4a
2) A = a2
Sustituyendo valores numéricos:
P = 4×6 = 24
A = 62 = 36
Los resultados llevan unidades arbitrarias.
Ejercicio 2: Hallar perímetro y área del cuadrado de lado “2a” y diagonal D = 20 unidades arbitrarias, que se muestra en la imagen
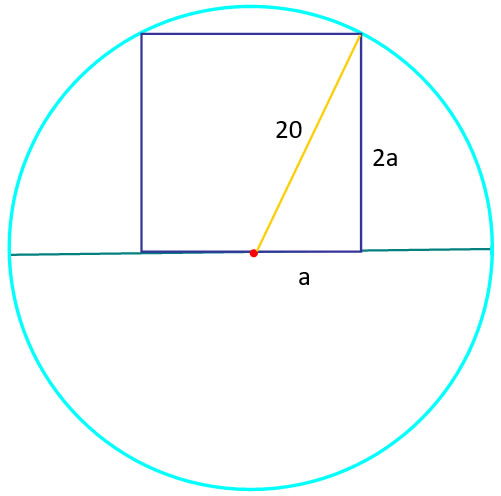
Respuesta
Dado que se forma un triángulo rectángulo de catetos “a” y “2a”, y se conoce el valor de la hipotenusa D = 20, se puede aplicar el teorema de Pitágoras:
\({{D}^{2}}={{a}^{2}}+{{\text{(2a)}}^{\text{2}}}=5{{a}^{2}}\)
Por lo tanto:
\(\text{a}=\sqrt{\frac{{{\text{D}}^{\text{2}}}}{\text{5}}}=\sqrt{\frac{{{20}^{2}}}{5}}=\sqrt{80}=4\sqrt{5}\)
El perímetro P es:
\(\text{P}=\text{4a}=\text{4}\times \text{4}\sqrt{\text{5}}=16\sqrt{5}\)
Y el área A es:
\(A={{a}^{2}}={{\left( 4\sqrt{5} \right)}^{2}}=16\times 5=80\)

Trabajo publicado en: Feb., 2021.