Definición de Trabajo Mecánico

Ingeniera Industrial, MSc en Física, y EdD
Desde el punto de vista de la física, el trabajo mecánico es la cantidad de energía que se transfiere cuando una fuerza mueve un objeto a través de una distancia en la dirección de dicha fuerza. Se define como el producto escalar de la fuerza aplicada \(\left( {\vec F} \right)\) y el desplazamiento resultante del objeto \(\left( \overrightarrow {Δr} \right)\) en la dirección de la fuerza.
La unidad de medida estándar del trabajo mecánico es el joule (J), que es igual a la energía transferida cuando se aplica una fuerza de un Newton (N) a un objeto y se lo mueve a través de una distancia de un metro (m) en la dirección de la fuerza.
El trabajo mecánico depende de la magnitud de la fuerza aplicada y la distancia a la que se mueve el objeto en la dirección de la fuerza, por lo que la fórmula para el trabajo mecánico es:
\(W = \vec F \cdot \overrightarrow {Δr} \)
Que es equivalente a:
\(W = F \cdot d \cdot cos\theta \)
donde W es el trabajo mecánico, F es la fuerza aplicada, d es la distancia recorrida y θ es el ángulo entre la dirección de la fuerza y el desplazamiento del objeto.
Es importante mencionar que el trabajo mecánico puede ser positivo o negativo, dependiendo de si la fuerza está en la misma dirección que el desplazamiento del objeto o en dirección opuesta.

En la imagen se muestra que el hombre que transporta la carretilla con la carga está realizando un trabajo desde el punto de vista de la física, ya la mayor parte de la fuerza que aplica sobre la carretilla va en la misma dirección del desplazamiento (horizontal).
Influencia del ángulo de aplicación de la fuerza en el trabajo
El ángulo de aplicación de la fuerza tiene una influencia en el trabajo mecánico que se realiza sobre un objeto. En la fórmula del trabajo mecánico W = F x d x cos(θ), el ángulo θ se refiere al ángulo entre la dirección de la fuerza aplicada y el desplazamiento del objeto.
Si el ángulo es de 0 grados, significa que la fuerza se aplica en la misma dirección en la que se mueve el objeto, entonces el trabajo mecánico es máximo y es igual a la fuerza por la distancia recorrida.
Si el ángulo es de 90 grados, implica que la fuerza se ejerce perpendicularmente a la dirección del movimiento, entonces el trabajo mecánico es cero.
Para ángulos menores de 90° el trabajo es positivo (fuerza a favor del desplazamiento), y para ángulos mayores a 90° y hasta 180°, el trabajo es negativo (la fuerza va en contra del movimiento).
En general, cuanto menor sea el ángulo entre la fuerza y el desplazamiento del objeto, mayor será el trabajo mecánico realizado. Por lo tanto, el ángulo de aplicación de la fuerza es un factor importante a considerar al calcular el trabajo mecánico en una situación dada.
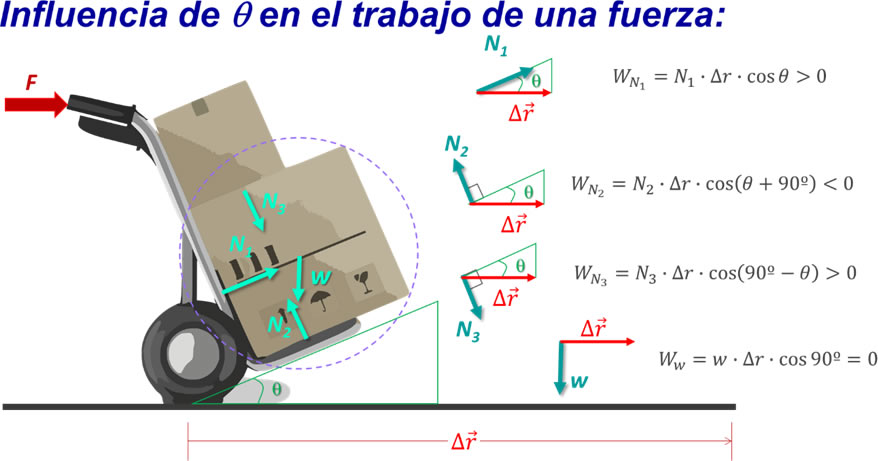
En la imagen se muestra una carretilla donde se transportan dos cajas. Si se analiza la caja más grande (que se encuentra debajo de la segunda caja), se observan que las fuerzas que actúan sobre ella son su peso, las dos normales que le ejercen las dos superficies de la carretilla donde se apoya, y la normal de la segunda caja. Del lado derecho se indica el trabajo que realiza cada una de estas fuerzas para el desplazamiento Δr.
Trabajo realizado por una fuerza variable
Para calcular el trabajo realizado por una fuerza variable, se puede dividir el desplazamiento del objeto en pequeños tramos iguales. Se supone que la fuerza es constante en cada tramo y se calcula el trabajo realizado en ese tramo mediante la ecuación del trabajo para una fuerza constante:
\(W = \vec F \cdot \overrightarrow {Δr} \)
donde \(\vec F\) es la fuerza en ese tramo y \(\overrightarrow {Δr} \) es el desplazamiento en ese tramo.
Luego, se suman los trabajos realizados en todos los tramos para obtener el trabajo total realizado por la fuerza variable a lo largo del desplazamiento del objeto. Este método es aproximado y puede perder precisión si existen variaciones significativas en la fuerza en diferentes puntos del desplazamiento. En tales casos, se puede utilizar el cálculo de integrales para obtener una solución más precisa, especialmente cuando la fuerza varía continuamente.
\(\sum W = {W_{neto}} = \smallint \left( {\sum \vec F} \right) \cdot d\vec r\)
Esta expresión indica que le trabajo mecánico representa el área bajo la curva en un diagrama de fuerza versus desplazamiento.
Trabajo de un resorte
Para calcular el trabajo realizado por un resorte se puede utilizar la ley de Hooke, la cual establece que la fuerza ejercida por un resorte es proporcional a la deformación del resorte; y la constante de proporcionalidad se denomina constante de resorte, representada por la letra k.
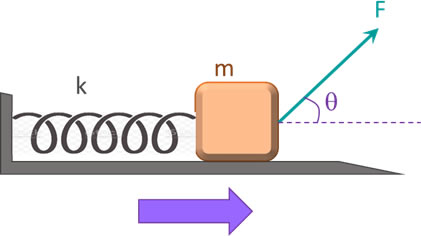
Los parámetros para determinar el trabajo mecánico efectuado sobre un resorte son su constante (k) y la magnitud de su deformación (x).
Primero se deben medir tanto la deformación del resorte (x) como la fuerza ejercida por él en cada punto a lo largo del desplazamiento. Luego se debe calcular el trabajo realizado por el resorte en cada tramo utilizando la expresión:
\({W_R} = \frac{1}{2} \cdot k \cdot {x^2}\)
donde k es la constante de resorte y x es la deformación en ese tramo. Finalmente, se deben sumar los trabajos realizados en todos los tramos para obtener el trabajo total realizado por el resorte.
Es importante destacar que el trabajo realizado por un resorte es siempre positivo, ya que la fuerza y el desplazamiento siempre actúan en la misma dirección.
Ejemplo de trabajo mecánico
Supongamos que un objeto de masa 2 kg se levanta verticalmente a velocidad contante 1 metro utilizando una cuerda. Como se observa en el siguiente diagrama, la fuerza de la cuerda se ejerce en la misma dirección que el desplazamiento del objeto hacia arriba y su magnitud es el peso, el cual se determina como el producto de la masa por la gravedad, que es de 19,62 N (aproximadamente 2 kg x 9,81 m/s2).

Para encontrar el trabajo mecánico, se aplica la expresión \(W = F \cdot d \cdot cos\theta \), donde θ es el ángulo entre la dirección de la fuerza aplicada y el desplazamiento del objeto, en este caso θ = 0° grados, puesto que tanto la tensión (T) como el desplazamiento van hacia arriba. Por lo tanto, se tiene:
W = F x d x cos(0) = 19,62 N x 1 m x 1 = 19,62 J
Este resultado indica que la tensión necesaria para levantar el objeto en contra de la gravedad, efectúa un trabajo mecánico de 19,62 joules.

Art. actualizado: Abril 2023; sobre el original de abril, 2023.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.