Definición de Triángulo

Ingeniera Industrial, MSc en Física, y EdD
Los triángulos son figuras geométricas compuestas por tres lados, tres ángulos internos y tres vértices. Los triángulos son unas de las figuras más estudiadas y utilizadas en Matemática, Física y otras áreas, ya que muchos análisis y teoremas utilizan a esta figura como base.
Una de las propiedades que cumplen todos los triángulos es que la suma de sus tres ángulos internos debe ser 180°. Así mismo, se cumple que en un vértice, la suma del ángulo interno más el ángulo externo es de 180°, es decir, son ángulos suplementarios. De acuerdo con lo anteriormente expuesto, en un triángulo solo puede haber, a lo sumo, un ángulo, ya sea obtuso o recto, y en ese caso, los otros dos ángulos son agudos.
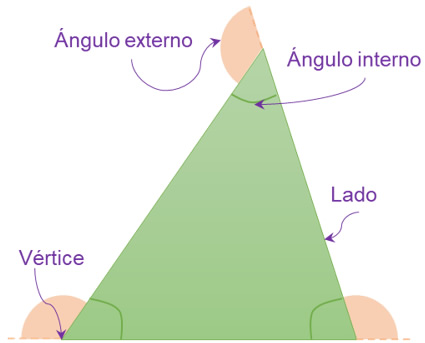
Los elementos principales que conforman a un triángulo son sus lados, sus ángulos y sus vértices.
Clasificación de los triángulos según sus lados
Existen diversos criterios para clasificar los triángulos, y uno de ellos es considerando sus lados. Bajo este criterio los triángulos pueden ser:
Equiláteros: son triángulos que poseen sus tres lados iguales y por ende, sus tres ángulos internos también son iguales (cada uno mide 60°).
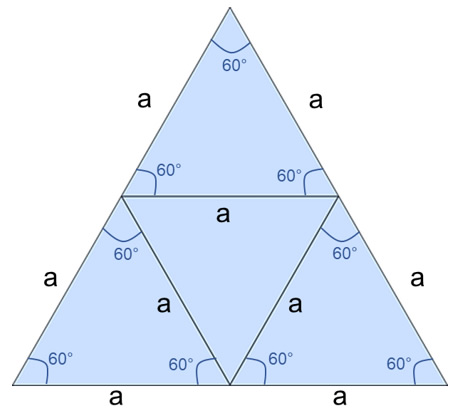
Todos los triángulos que se muestran en la figura son equiláteros. Los triángulos pequeños tienen lados de longitud “a”, mientras que el triángulo más grande (que contiene a todos los triángulos pequeños) tiene lados de medida “2a”.
Isósceles: son los triángulos que poseen dos lados iguales y uno diferente. Igualmente, los dos ángulos internos adyacentes al lado diferente son iguales, y el ángulo interno formado por la intersección de los dos lados iguales es diferente.
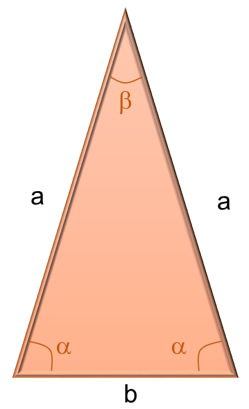
En la figura se muestra in triángulo isósceles. Como se observa, posee los dos lados laterales iguales, con media “a” cada uno, y un lado desigual que mide “b”. También se cumple que, dos de sus ángulos internos son iguales y otro diferente.
Escaleno: este triángulo posee sus tres lados con medidas diferentes, al igual que sus tres ángulos internos.
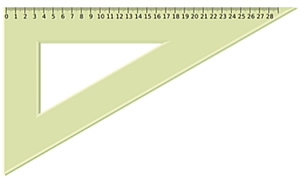
En la figura se muestra un cartabón que posee tres lados con medidas diferentes, por lo que se trata de un triángulo escaleno. El cartabón forma un triángulo particular, porque además es rectángulo y sus ángulos internos son 60°, 30° y 90°.
Clasificación de los triángulos según sus ángulos
Otro criterio comúnmente empleado para clasificar los triángulos, es considerando sus ángulos internos, en cuyo caso, los triángulos pueden ser:
Rectángulos: también llamado triángulos rectos, se caracterizan por tener un ángulo recto (de 90°) y los otros dos ángulos agudos (menores de 90°). El lado opuesto al ángulo recto en un triángulo rectángulo es el más largo y se denomina hipotenusa, y sus otros lados se llaman catetos. Este triángulo es de gran importancia en Matemática, ya que las relaciones trigonométricas, el teorema de Pitágoras, la ley del coseno y otras relaciones se basan en este tipo de triángulo.
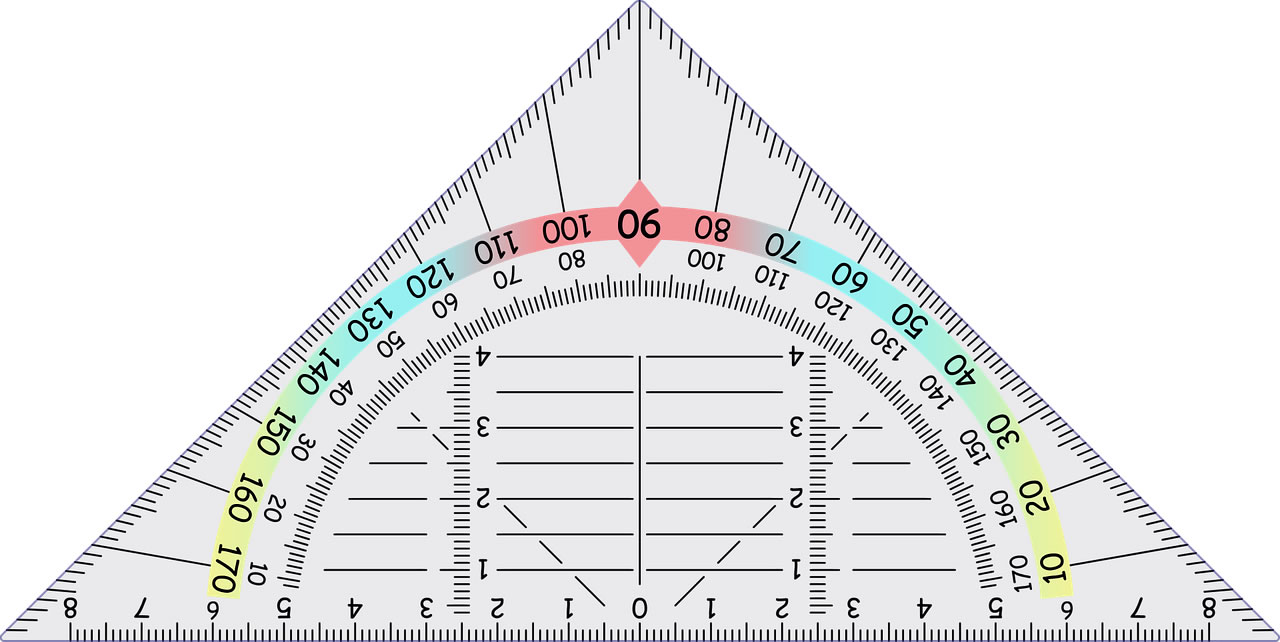
La figura muestra una escuadra básica en los juegos geométricos. En particular forma un triángulo isorectángulo, lo que significa que tiene un ángulo interno de 90° y los otros dos de 45° cada uno. También posee dos lados iguales y uno diferente.
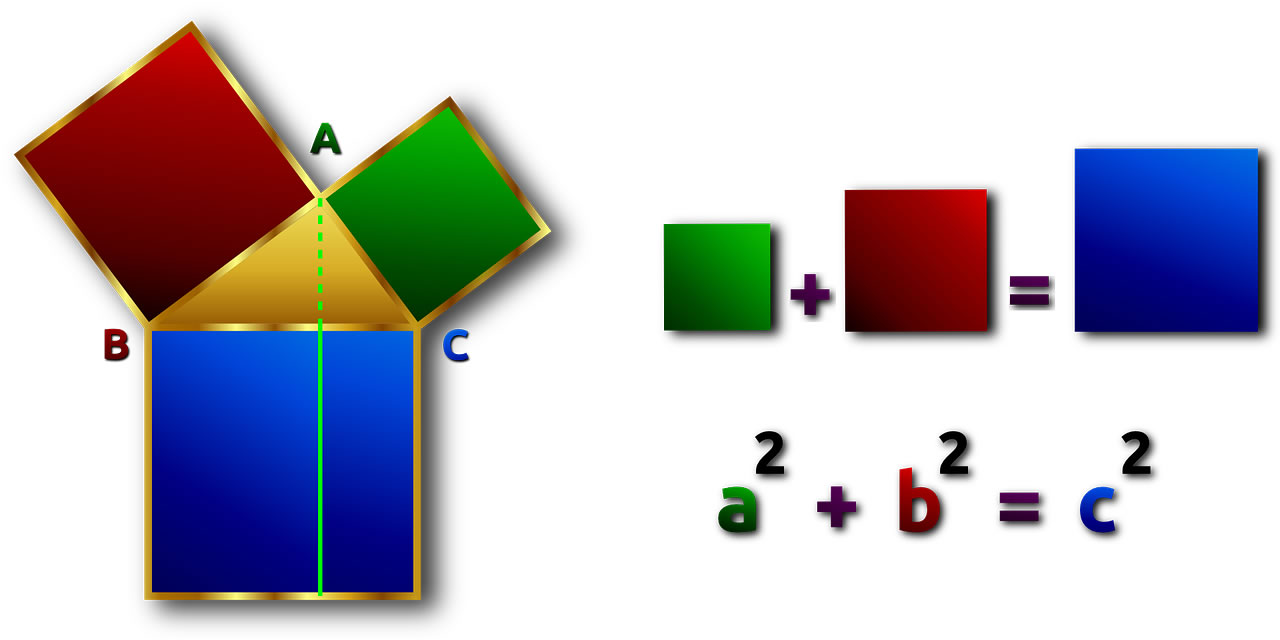
El teorema de Pitágoras plantea que en un triángulo rectángulo, siempre se cumple que el cuadrado de la hipotenusa es igual a la suma del cuadrado de sus catetos.
Acutángulo: son triángulo que poseen sus tres ángulos internos menores de 90°, es decir, que sus tres ángulos son agudos. Esto significa que todo triángulo equilátero es también acutángulo.

Muchos símbolos de seguridad y precaución son representados utilizando la figura de un triángulo como base. El triángulo que se muestra en la imagen es una señal de advertencia y el contorno de color rojo representa un triángulo acutángulo.
Obtusángulo: Son los triángulos que poseen un ángulo interno obtuso, es decir, mayor de 90°, y los otros dos ángulos internos son agudos.
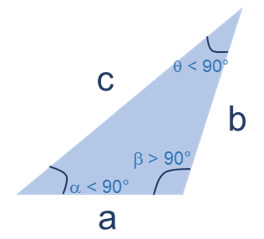
La característica del triángulo obtusángulo es la presencia de un ángulo interno obtuso, es decir, mayor de 90° y menor de 180°.
Desigualdad triangular
La desigualdad triangular también se conoce como desigualdad de Minkowski, y se refiere a la relación de lados que deben cumplir en todo triángulo:
La suma de dos lados de un triángulo siempre tiene que ser mayor al tercer lado.

Para cualquier triángulo, si se toman las rectas que conforman cada uno de sus tres lados, se puede observar que siempre, la suma de la longitud de dos de sus lados, es mayor que la del lado restante.
Rectas notables en los triángulos
En los triángulos, existen algunas medidas o rectas que los caracterizan, básicamente se trata de la altura, la mediana, la mediatriz, y la bisectriz. Cada triángulo posee tres de cada una de estas rectas.
La altura (h): representa la distancia que va desde un vértice y se proyecta perpendicular hasta el lado opuesto.
La mediana (M): son las rectas que van desde un vértice y se proyectan a la mitad del lado opuesto.
La mediatriz (m): es la recta que incide perpendicular a cada lado del triángulo pasando por el punto medio de dicho lado.
La bisectriz (B): es la recta sale de cada vértice, bisecando el ángulo interno de dicho vértice.
Puntos notables en los triángulos
Así como existen rectas notables en los triángulos, también hay puntos notables asociados a estas rectas, que son el baricentro, el ortocentro, el circuncentro y el incentro.
El ortocentro (o), es el punto donde se cortan las tres alturas de un triángulo.
El baricentro (b), es el punto donde convergen las tres medianas de un triángulo.
El circuncentro (c), este punto se forma por la intersección de las mediatrices de un triángulo. Puede estar dentro o fuera del triángulo, (como en el caso de los obtusángulos). El cincuncentro es el centro de una circunferencia que se encuentra circunscrita en el triángulo.
El incentro (i), es el punto en el cual convergen las bisectrices de un triángulo. Este punto es el centro de una circunferencia inscrita dentro del triángulo.
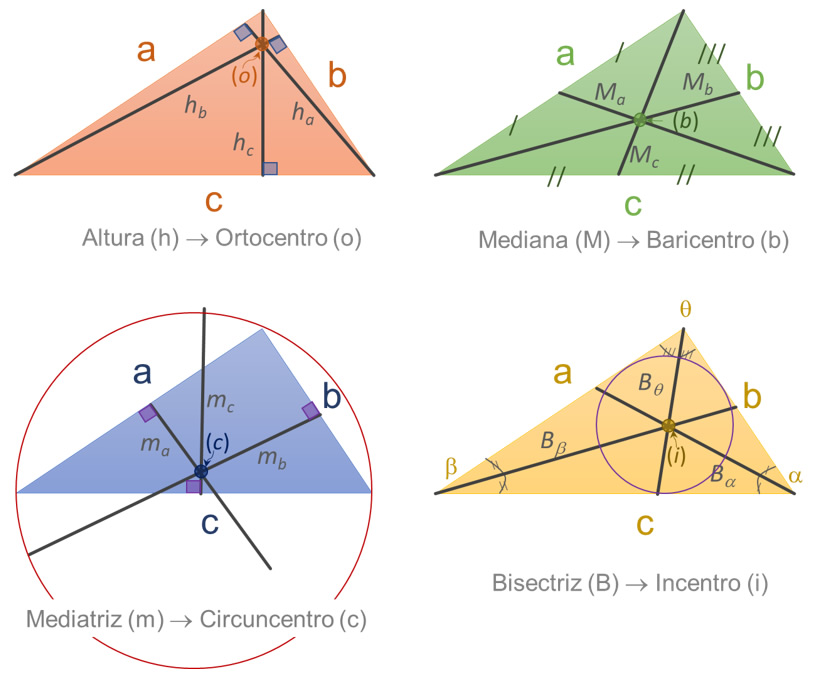
La imagen muestra las rectas y puntos notables en los triángulos.
Área y perímetro de un triángulo
Ya conocidos los parámetros y rectas notables de los triángulos, se pueden establecer las ecuaciones para determinar su área y perímetro. El área (A) es la región interna delimitada por sus tres lados, y se calcula a partir de su base (b) y altura (h) con la expresión:
\(A = \frac{{b \cdot h}}{2}\)
Considerando a los lados del triángulo con medidas a, b y c, el perímetro (P), se determina con la suma de sus tres lados, es decir:
\(P = a + b + c\)
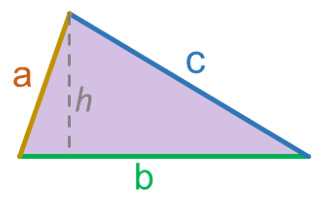
Parámetros para determinar el área y altura de un triángulo.

Art. actualizado: Dic. 2022; sobre el original de julio, 2009.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.