Significado de aceleración Definición, cálculo, dirección y sentido

Licenciada en Física
Definición formal
La aceleración es el vector que describe y cuantifica los cambios en la velocidad de un móvil. Puesto que la velocidad también es un vector, sus cambios pueden ser de magnitud, de dirección y sentido, o todos a la vez.
Se trata de una magnitud fundamental en la Cinemática y que además forma parte de multitud de situaciones familiares: está presente en el arranque de un automóvil cuando la luz del semáforo cambia a verde, la tiene un delantero que corre con la pelota, y se la puede experimentar a diario, como el vuelco que se siente en el estómago al subir o bajar en ascensor.
Asimismo, los seres vivos se encuentran inmersos en el campo gravitatorio de la Tierra, cuya intensidad es más o menos constante (en realidad sí experimenta algunas variaciones) y se conoce como g, el valor de la aceleración de la gravedad terrestre.
La aceleración no es sinónimo de velocidad, aunque estén estrechamente relacionadas. Una gran aceleración no implica necesariamente que un móvil se mueva muy rápido. Por ejemplo, un automóvil puede desplazarse a 200 km/h sobre una autopista recta, y tener aceleración 0, si su velocidad no está cambiando. Y, por el contrario, se puede ir muy despacio, pero teniendo una gran aceleración, como cuando el automóvil arranca bruscamente ante un cambio en la luz del semáforo o si frena repentinamente.
La aceleración tiene unidades de velocidad sobre tiempo. En el Sistema Internacional, la velocidad viene en m/s, por lo tanto, la aceleración expresa en m/s2. Por ejemplo, una aceleración de 4 m/s2 significa que por cada segundo que pasa, el móvil cambia su velocidad en 4 m/s. Otras combinaciones de unidades son posibles también, como km/h∙s o millas/ h∙s. Una aceleración de 0.5 km/h∙s se interpreta así: el móvil cambia su velocidad en 0.5 km/h cada segundo que pasa.
Cálculo de la aceleración media
La aceleración se puede expresar de forma matemática mediante su definición. Supóngase que un móvil tiene una velocidad inicial llamada vo en el instante to. La velocidad se denota en texto impreso con letra negrita o con una flecha encima, para diferenciarla de una cantidad escalar como el tiempo y es preciso siempre hacer la distinción, pues los vectores tienen una naturaleza muy diferente que la de los escalares.
Si un tiempo después, en el instante tf, la velocidad del móvil en cuestión pasa a ser vf, como la aceleración es la variación de la velocidad durante el lapso de tiempo en que tal variación ocurre, se define la aceleración media am como:
\({{\vec{a}}_{m}}=\frac{{{{\vec{v}}}_{f}}-{{{\vec{v}}}_{o}}}{{{t}_{f}}-{{t}_{o}}}\)
La diferencia entre una cantidad final y una cantidad inicial se denota de forma más compacta con ayuda de la letra griega Δ (se lee “delta”). Gracias a esta notación, la aceleración media se escribe también así:
\({{\vec{a}}_{m}}=\frac{\Delta \vec{v}}{\Delta t}\)
Aceleración instantánea
La aceleración media, definida arriba, indica el cambio de velocidad en un instante de tiempo mensurable Δt. Pero sería mejor si se conociera la aceleración en cada instante del movimiento, por eso, si ese intervalo se hace muy, muy pequeño, se tendría la aceleración instantánea, es decir, la aceleración en un instante cualquiera.
Matemáticamente, hacer que Δt se haga muy pequeño significa tomar el límite de Δt cuando tiende a 0, sin que llegue realmente a valer 0. Con esto en mente, la aceleración instantánea o simplemente aceleración a de un móvil es:
\(\vec{a}=\underset{\Delta t\to 0}{\mathop \lim }\,\frac{\Delta \vec{v}}{\Delta t}\)
A este límite se lo conoce como la derivada de la velocidad respecto al tiempo. Una derivada es la tasa de cambio de una magnitud respecto a alguna variable, como puede ser el tiempo, entonces:
\(\vec{a}=\frac{d\vec{v}}{dt}\)
Geométricamente, la derivada de una cantidad respecto a una variable, se interpreta como la pendiente de la recta tangente a la curva que representa la cantidad en función de dicha variable, en un determinado punto.
Representando la función velocidad en función del tiempo en una gráfica, su derivada en el punto P corresponde a la pendiente de la recta que pasa por el punto de tangencia P de la siguiente figura:
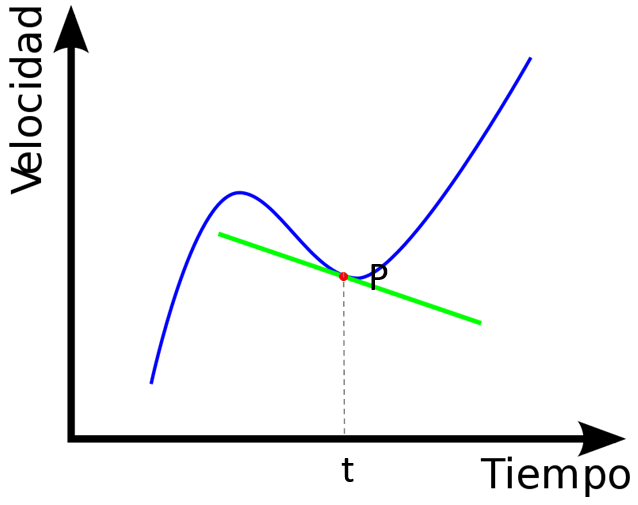
Otra notación muy utilizada para la derivada, aparte de la ya mostrada, es la notación con primas, de modo que la aceleración también se puede escribir como:
a = v´(t)
Dirección y sentido de la aceleración
La dirección y el sentido de la aceleración son tan importantes como su magnitud o valor numérico. De eso depende el tipo de movimiento.
La aceleración puede tener la misma dirección que la velocidad o puede tener otra dirección cualquiera. Si la aceleración es no nula y tiene la misma dirección que la velocidad, la dirección de esta no cambia, pero sí lo hace su magnitud. Puede que el móvil frene o que vaya cada vez más rápido, dependiendo del sentido de la aceleración.
Para ilustrar este hecho, supóngase un automóvil que se dirige el este a razón de 90 km/h. Si tiene una aceleración que también apunta hacia el este, quiere decir el automóvil aumenta la magnitud de su velocidad (su rapidez), por lo que el conductor está oprimiendo el pedal del acelerador.
En cambio, si la aceleración se dirige hacia el oeste, es que el conductor está pisando el freno y la rapidez del vehículo va disminuyendo. Para distinguir entre ambas posibilidades se usan los signos, por ejemplo hacia el este puede ser signo + y hacia el oeste signo −.
Pero en todo caso, el movimiento se mantiene rectilíneo, ya que la aceleración no está cambiando la dirección de la velocidad de ninguna forma, tan solo su magnitud. El movimiento así descrito se conoce como movimiento rectilíneo uniformemente variado.
Sin embargo, hay que resaltar el hecho de que la aceleración describe cualquier cambio en la velocidad.
¿Qué pasa si un móvil tiene aceleración constante, pero en dirección perpendicular a su velocidad? Ocurre que el móvil no experimentaría un cambio en su rapidez, lo que quiere decir que si se movía a razón de 90 km/h seguirá manteniendo esa misma rapidez. Pero dejaría de ir en línea recta, en caso de hubiera estado viajando así, porque esta aceleración perpendicular le obliga a dar una trayectoria curva.
Y si antes el móvil se desplazaba en línea recta, ahora lo hará con movimiento circular uniforme (siempre que la aceleración se mantenga perpendicular a la velocidad y con magnitud constante).
En general un automóvil que circula por una carretera experimenta un movimiento curvilíneo variado, por lo tanto, según los tramos de la vía, su aceleración puede tener componentes en varias direcciones para adaptarse a la trayectoria.

Trabajo publicado en: Ene., 2021.