Distancia Recorrida y Desplazamiento - Definición, Concepto y Qué es

Ingeniera Industrial, MSc en Física, y EdD
1.A. La distancia recorrida es una cantidad escalar representada por un valor numérico seguido de una unidad de medida que responde a la recorrido total entre dos puntos, es decir, es la suma de todos los desplazamientos que realiza un objeto en movimiento hasta llegar a su destino. Este valor siempre es positivo, ya que para este cálculo es indiferente la dirección en la que se mueve el objeto, solo se considera la longitud del camino.
1.B. El desplazamiento: es una cantidad vectorial que representa la distancia más corta entre dos puntos considerando las posiciones inicial y final del objeto. Su magnitud puede aumentar o disminuir en función de la trayectoria por la que se desplace el objeto, es decir, si este objeto se desplaza hacia atrás desde el punto de partida, este desplazamiento será negativo y cualquier movimiento hacia adelante será positivo.
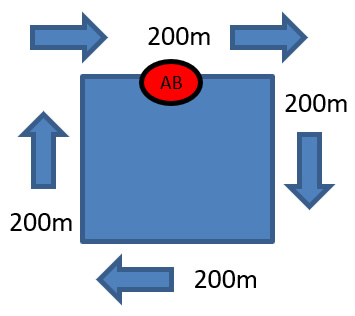 Ejemplo práctico: Una persona paseando por el patio de tu casa. Los puntos A (inicial) y B (final) son iguales y cada parte de la cancha equivale a 1 km. En este escenario, la distancia recorrida será 800m = 800 (Valor numérico) y m (metro - unidad de medida estándar); el desplazamiento será 0 (cero) m.
Ejemplo práctico: Una persona paseando por el patio de tu casa. Los puntos A (inicial) y B (final) son iguales y cada parte de la cancha equivale a 1 km. En este escenario, la distancia recorrida será 800m = 800 (Valor numérico) y m (metro - unidad de medida estándar); el desplazamiento será 0 (cero) m.
Etimología: Distancia, por el latín distantia, marcado por el prefijo dis-, en función de ‘separar’, ‘alejar’, seguido del verbo stare, de ‘estar’, y el sufijo -ncia, conforme la sustantivación; recorrida, sobre el verbo recorrer, por el latín recurrĕre; desplazamiento, por el verbo desplazar, sobre el prefijo des-, en cuanto ‘distintas direcciones’, y plaza, con referencia en el latín platĕa, respecto del griego πλατεῖα (plateîa), por ‘ancha’ respecto de un área amplia.
Cat. gramatical: Sustantivo masc / fem. respectivamente.
En sílabas: dis-tan-cia + re-co-rri-da + des-pla-za-mien-to.
Distancia Recorrida y Desplazamiento
Para comprender los conceptos de distancia recorrida y deslazamiento, es necesario primero definir el término posición, que no es más que un vector que indica la ubicación de una partícula o punto con respecto a un sistema de referencia. De lo anterior, se puede definir la distancia recorrida como un escalar que expresa la longitud de la trayectoria cuya descripción se basa en una partícula que va de un punto inicial a un punto final. Por otra parte, el desplazamiento, es un vector que mide el cambio de posición de una partícula al moverse de un punto inicial a un punto final, y es independiente de la trayectoria.
Distancia recorrida
Tanto la posición, como la distancia recorrida y el desplazamiento tienen unidades de longitud, esto es, metros, kilómetros, pulgadas, yardas, pies, etc.; sin embargo, desde el punto de vista conceptual, son cantidades físicas diferentes y de gran utilidad para explicar la Física en todas sus áreas. Por ejemplo, la cinemática es el área de la Física responsable por entender el movimiento de los cuerpos independientemente de las causas, por lo tanto, se requiere de estos términos para analizar el movimiento de las partículas o cuerpos.
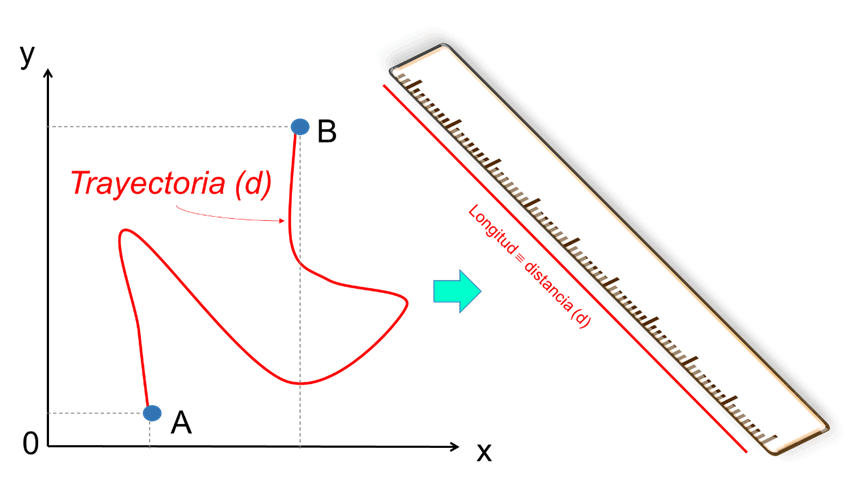
Por ejemplo, si se estudia una partícula (considerada como un punto geométrico) que se mueve de un punto A hasta un punto B como se muestra en la imagen, siendo “0” el origen de un sistema de referencia arbitrario, la distancia recorrida será la medida de la línea de color rojo. En la práctica, significaría tomar la línea roja, enderezarla y medir su longitud. Evidentemente, al cambiar la ruta de la trayectoria, cambiaría la distancia recorrida. Asimismo, la menor distancia para ir de un punto a otro, sería en línea recta.
Los vectores de posición \(\vec{r}\):
Si en el ejemplo anterior se desea especificar la posición de la partícula en los puntos A y B, se deben trazar dos vectores: el vector posición de A \(\left( {{{\vec{r}}}_{A}} \right)\), va desde el origen del sistema de referencia “0” con coordenadas (0, 0), hasta el punto A, de coordenadas (xA, yA). Análogamente, el vector posición del punto B \(\left( {{{\vec{r}}}_{B}} \right)\), va desde el origen del sistema de referencia “0” con coordenadas (0, 0), hasta el punto B, de coordenadas (xB, yB). Estos vectores se muestran en la imagen en color azul:
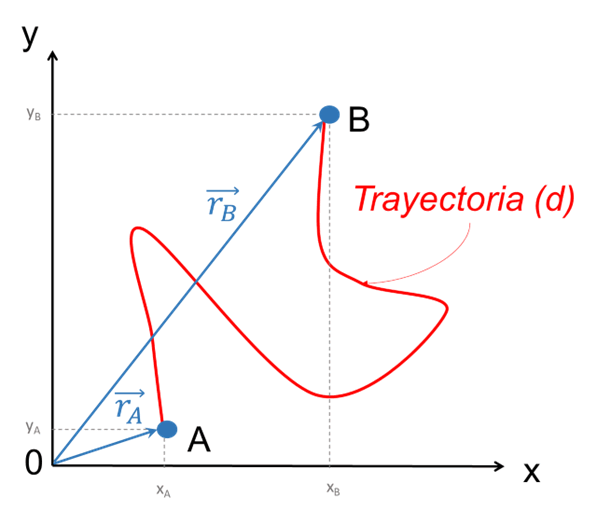
Para determinar las componentes de cada vector posición, simplemente se deben restar las coordenadas del punto final vector menos las coordenadas del punto inicial del vector:
\({{\vec{r}}_{A}}=A-0=\left( {{x}_{A}},~{{y}_{A}} \right)~unidades-~\left( 0,~0 \right)~unidades~\to ~{{\vec{r}}_{A}}=\left( {{x}_{A}}\hat{i},~{{y}_{A}}\hat{j} \right)~unidades\)
\({{\vec{r}}_{B}}=B-0=\left( {{x}_{B}},~{{y}_{B}} \right)~unidades-~\left( 0,~0 \right)~unidades~\to ~{{\vec{r}}_{B}}=\left( {{x}_{B}}\hat{i},~{{y}_{B}}\hat{j} \right)~unidades\)
Es importante destacar que la posición es una cantidad física vectorial que se expresa en unidades de longitud, por lo que siempre el vector debe estar acompañado de sus correspondientes unidades.
Nota: cuando se hace referencia a la ubicación de un punto en el espacio, se utilizan “coordenadas” y éstas se deben expresar en paréntesis, usualmente separadas con coma (o punto y coma). En el caso de los vectores expresados a través de sus “componentes” rectangulares, lo más recomendable es indicar en cada componente el vector unitario que indica la dirección de la misma: \(\hat{i}\) para la dirección en el eje x, \(\hat{j}\) para la dirección en el eje y y \(\hat{k}\) para la dirección en el eje z.
Desplazamiento \(\left( \overrightarrow{\Delta r} \right)\)
Continuando con el ejemplo anterior, si ahora se desea conocer el desplazamiento \(\overrightarrow{\Delta r}\) de la partícula al moverse del punto A, hasta el punto B, solo se debe restar el vector de posición final (en este caso \({{\vec{r}}_{B}}\)) menos el vector de posición inicial (\({{\vec{r}}_{A}}\)). Como se observa en el siguiente gráfico, el desplazamiento representado con el vector verde (\(\overrightarrow{\Delta r}\)) es independiente de la trayectoria recorrida y solo depende los puntos extremos (inicial y final):
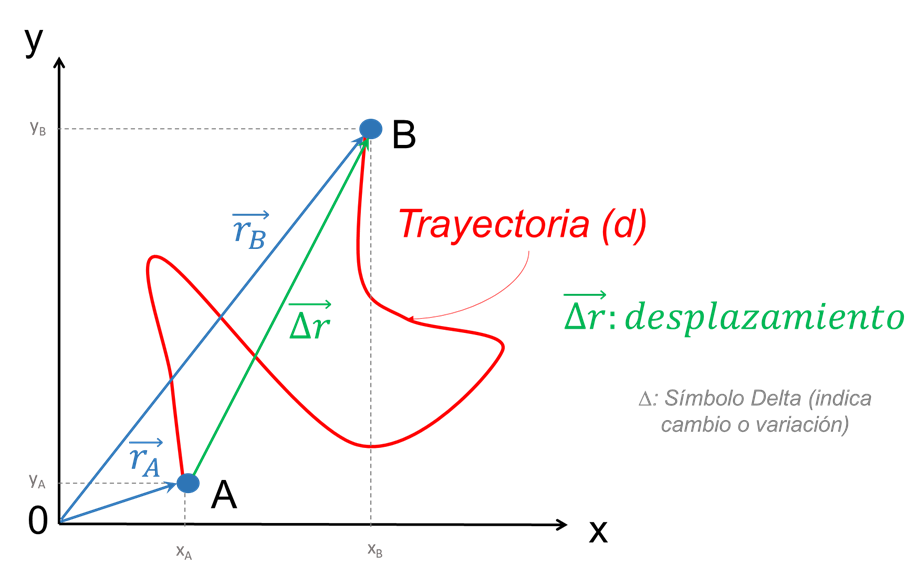
\(\overrightarrow{\Delta r}={{\vec{r}}_{B}}-{{\vec{r}}_{A}}=\left( {{x}_{B}}\hat{i},~{{y}_{B}}\hat{j} \right)-\left( {{x}_{A}}\hat{i},~{{y}_{A}}\hat{j} \right)=\left[ \left( {{x}_{B}}-{{x}_{A}} \right)\hat{i}+\left( {{y}_{B}}-{{y}_{A}} \right)\hat{j} \right]~unidades\)
\(\overrightarrow{\Delta r}=\left( \Delta x\hat{i}+~\Delta y\hat{j} \right)~unidades\)
Cuando la trayectoria descrita por la partícula para ir del punto inicial al punto final es una línea recta, solo en ese caso, la distancia recorrida es igual al módulo del vector desplazamiento. En general, se puede afirmar que:
\(d\ge \left| \overrightarrow{\Delta r} \right|\)
Para comprender mejor la diferencia entre la distancia recorrida y el desplazamiento, se presenta el siguiente ejemplo con valores numéricos. Supongamos que una partícula se mueve del punto A al punto B de acuerdo con la trayectoria y coordenadas que se muestran en la figura:
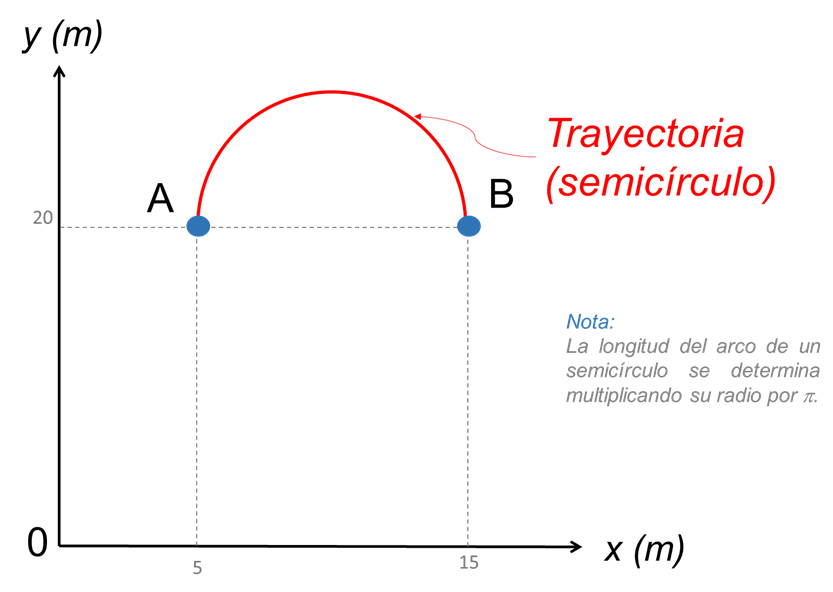
La distancia recorrida (d) es la longitud del arco de semicírculo:
\(d=\pi \cdot r\)
Donde r es la mitad del diámetro, que de acuerdo con la imagen, el diámetro es (15 m – 5 m = 10 m), por lo tanto el radio es de 5 m.
\(d=\pi \cdot \left( 5~m \right)=15.71~m\)
Por otra parte, los vectores de posición serán:
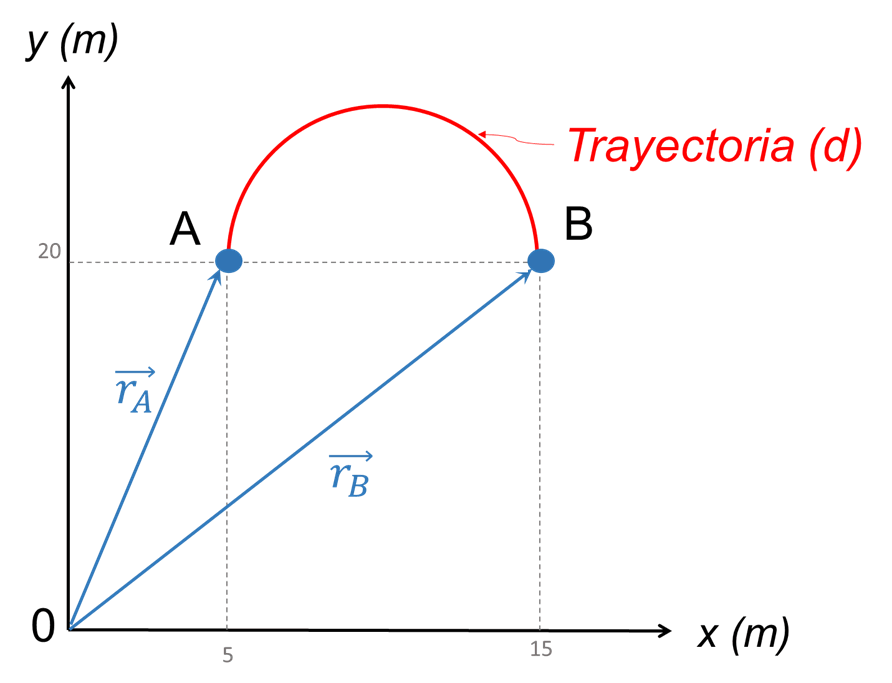
\({{\vec{r}}_{A}}=\left( 5,~20 \right)m-\left( 0,~0 \right)m=\left( 5\hat{i}+20\hat{j} \right)~m\)
\({{\vec{r}}_{B}}=\left( 15,~20 \right)m-\left( 0,~0 \right)m=\left( 15\hat{i}+20\hat{j} \right)~m\)
Finalmente, el desplazamiento \(\overrightarrow{\Delta r}\) representa el cambio de posición, y se determina:
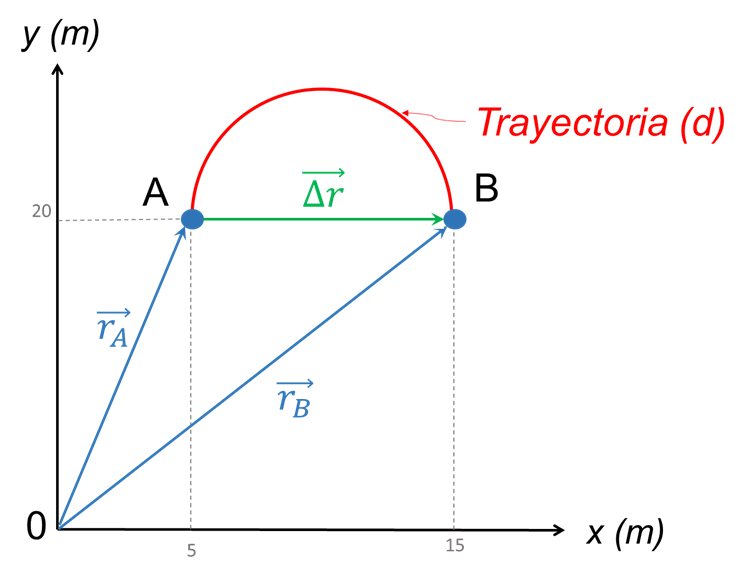
\(\overrightarrow{\Delta r}={{\vec{r}}_{B}}-{{\vec{r}}_{A}}=\left( 15\hat{i}+20\hat{j} \right)~m-\left( 5\hat{i}+20\hat{j} \right)~m\)
\(\overrightarrow{\Delta r}=\left( 10\hat{i}+0\hat{j} \right)~m\)
El módulo del vector desplazamiento se determina mediante el Teorema de Pitágoras:
\(\left| \overrightarrow{\Delta r} \right|=\sqrt{{{10}^{2}}+{{0}^{2}}}=10~m\)
Se demuestra que \(d\ge \left| \overrightarrow{\Delta r} \right|\).

Art. actualizado: Junio 2022; sobre el original de abril, 2017.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.