Significado de estática Definición, características, y ejercicios

Licenciada en Física
Definición formal
La estática es la responsable por descifrar y revelar el equilibrio de los cuerpos, rigiéndose por la Primera Ley de Newton, la cual asegura que si un cuerpo está libre de interacciones con otros, entonces está en equilibrio estático. Esto no significa que el cuerpo esté necesariamente en reposo. Un cuerpo en equilibrio estático puede tener velocidad nula o moverse con velocidad traslacional y rotacional uniforme, siempre que sea observado desde un marco de referencia inercial.
Puede decirse que un cuerpo está en equilibrio estático cuando la aceleración traslacional y la aceleración angular de rotación es nula respecto de un sistema de referencia inercial, que generalmente es un sistema fijo a tierra.
Sin embargo, con mucha frecuencia interesa el caso de equilibrio en el que el cuerpo está en absoluto reposo respecto a un referencial fijo, por ejemplo al construir estructuras estables como edificaciones, puentes y vías. De allí la importancia que adquiere la estática en las disciplinas propias de la ingeniería.
Características: Interacción y equilibrio
En la estática, la interacción de un objeto con otro se expresa matemáticamente mediante una cantidad vectorial denominada “fuerza”. La imagen muestra las fuerzas que actúan sobre una manzana en reposo sobre una mesa, representadas con flechas, un esquema conocido como “diagrama de cuerpo aislado”.
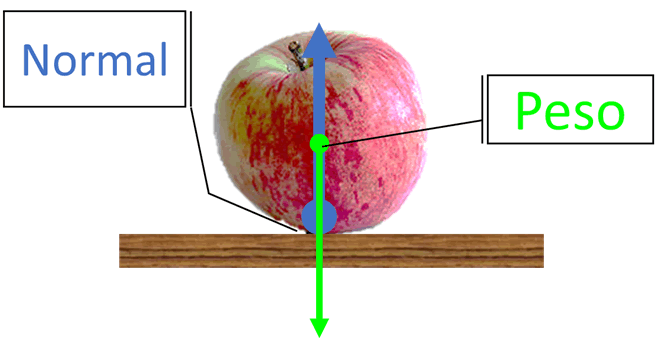
La interacción de una manzana con la Tierra se expresa mediante la fuerza conocida como peso, que siempre apunta hacia el centro del planeta y cuya intensidad es proporcional a la masa de la manzana (en color verde en la imagen). La constante de proporcionalidad es la aceleración de gravedad, que es la aceleración respecto al suelo que adquiere un cuerpo no equilibrado, librado únicamente a su propio peso.
Cuando la manzana está sobre la mesa permanece en reposo y por tanto está en equilibrio estático. Esto indica que además de la interacción con el planeta expresada a través el peso, existe sin duda otra interacción que mantiene el equilibrio de la manzana, la cual es ejercida por la mesa.
Esta interacción proviene del hecho de que la manzana no puede traspasar la superficie de la mesa, debido a una repulsión de origen electromagnético entre los átomos superficiales de la manzana y los de la mesa.
Desde el punto de vista clásico, la interacción entre la manzana y la mesa es una repulsión por “contacto”, llamada “fuerza normal”. Esta se expresa como una única fuerza que actúa sobre la manzana en el punto de contacto y apunta perpendicularmente a la superficie de la mesa y hacia arriba, tal como aparece reflejado en la imagen (flecha azul).
Condiciones de equilibrio
Para que la manzana esté en equilibrio es necesaria la siguiente condición: La suma vectorial del peso y la fuerza normal debe ser nula. Esto conduce a que tanto la normal como el peso deben tener la misma intensidad, pero direcciones opuestas, garantizando, de esta forma, el equilibrio traslacional de la manzana.
Sin embargo, no garantiza el equilibrio rotacional, ya que aun cuando las fuerzas sean iguales y contrarias, si estas no estuviesen aplicadas sobre la misma línea vertical, entonces la manzana volcaría.
Por la razón señalada antes, para el equilibrio de un cuerpo no es suficiente que todas las fuerzas que actúen sobre el mismo sumen cero, es necesario además que la suma de torques o momentos también se anule.
El torque
En física, el torque o momento respecto de un punto es una cantidad vectorial que se define como el producto de la fuerza por el brazo, siendo este último la distancia desde el punto hasta la recta o línea sobre la que actúa la fuerza. La dirección del torque es perpendicular a la fuerza y al vector que va del centro de torque hasta su punto de aplicación.
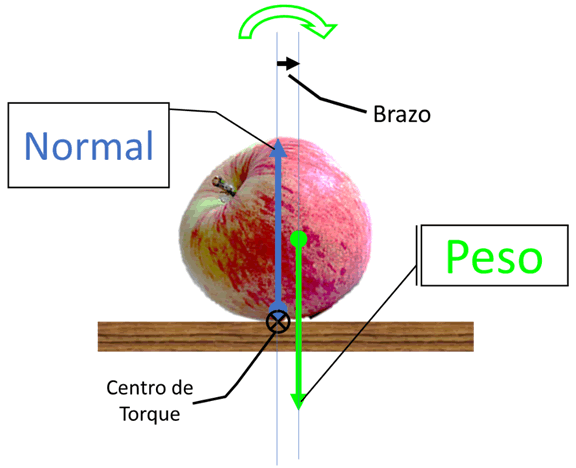
En la figura de arriba el peso hace torque respecto del punto de contacto. El vector torque apunta hacia adentro de la pantalla produciendo una rotación en el sentido horario.
En este caso la manzana no está en equilibrio estático aún cuando las fuerzas se anulan, ya que la suma de los torques no es cero. Si la manzana vuelca y se alinea el centro de gravedad con el punto de contacto, entonces se restaura el equilibrio tal como se ve en la primera figura, ya que en este caso se cumplen las dos condiciones de equilibrio: suma de fuerzas cero y suma de torques cero.
∑ Fuerzas es nula
∑ Momentos es nula
Ejercicios de aplicación
Ejercicio 1: una esfera lisa apoyada contra la pared
Una esfera completamente lisa se apoya de una pared vertical, colgada de una cuerda sujeta a la parte superior de la pared en un punto que está a una altura L= 1m, medido respecto al punto de contacto de la esfera con la pared. El radio de la esfera es R= 0,3m y su peso es de magnitud P= 5kg-f.
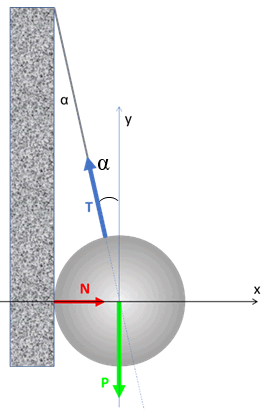
¿Cuáles son los respectivos valores de la fuerza normal y la tensión de la cuerda?
Lo primero que se debe notar es que la línea de acción de todas las fuerzas que actúan sobre la esfera pasa por el centro de la misma, lo cual garantiza que la sumatoria de torques respecto al centro es nula. Por lo tanto, solo hay que ocuparse del equilibrio traslacional.
En la dirección vertical se tiene el peso, el cual se equilibra con la componente vertical de la tensión, que es:
Ty= T∙cos α = P
Por lo tanto, como P = m∙g, queda:
\(T=\frac{P}{\cos \alpha }=\frac{m\cdot g}{\cos \alpha }\)
Por otra parte, la normal se equilibra con la componente horizontal de la tensión, de modo que la normal tiene magnitud:
N= T∙sen α
Además, se sabe que:
\(\tan \alpha =\frac{R}{L}\)
Luego:
\(\tan \alpha =\frac{0.3}{1}=0.3\)
De lo anterior se deduce que:
– El ángulo α vale 16,7º
– La tensión de la cuerda es: T = 5 kg-f / cos 16,7º = 5,2kg-f
– La fuerza normal es: N = 5,2 kg-f ∙sen 16,7º = 1,5kg-f.
Ejercicio 2: ubicación del punto de apoyo de un balancín
En los extremos de un listón de madera se cuelgan sendos pesos de P1= 5kg-f y P2= 3kg-f. Si el listón tiene longitud L= 2m, determine la distancia respecto de P1 a la que debe colocarse el punto de apoyo para que el balancín quede equilibrado.

Para el equilibrio del balancín es necesario que el torque respecto del punto de apoyo de cada uno de los pesos sea de igual magnitud y tengan direcciones contrarias.
Llamando x a la distancia de P1 al punto de apoyo, el torque será entonces P1∙x para la primera pesa.
La segunda pesa tiene un torque en la dirección opuesta de magnitud P2∙(L – x) y como los torques deben tener igual magnitud:
P1∙x = P2∙(L – x)
De donde se obtiene, mediante despeje, el valor de x:
\(x=\frac{{{\text{P}}_{\text{2}}}\text{ }\!\!\cdot\!\!\text{ L }}{{{\text{P}}_{\text{1}}}\text{ }+\text{ }{{\text{P}}_{\text{2}}}}\)
Al sustituir valores numéricos:
x = 3∙2 / (5 + 3)= 6/8 m= ¾ m= 0,75m

Trabajo publicado en: Abr., 2021.