Significado de funciones inyectivas, sobreyectivas y biyectivas Definición, y ejemplos

Licenciada en Física
Definición formal
Identifican y diferencian tres modalidades de funciones, de acuerdo a las formas de asociación observadas desde los elementos que constituyen el dominio (x), hacia aquellos del co-dominio (y). De este modo, 1) las inyectivas comprenden la presencia de un vínculo puntual para cada agente de x, sin registrarse coincidencias en y, 2) las sobreyectivas responden a aquellas en las cuales el co-dominio y el recorrido resultan en el mismo conjunto, y 3) las biyectivas ocurren cuando se advierten las dos situaciones y propiedades anteriores.
Para abordar el análisis, conviene refrescar primero ciertos conceptos relativos a las funciones, entendiéndose como una relación entre dos conjuntos de elementos, tal que, a través de una regla de correspondencia, a cada elemento del conjunto de partida se le asigna una imagen única en el conjunto de llegada. Los elementos de ambos conjuntos no necesariamente son numéricos, sin embargo, para modelar los fenómenos del mundo real, frecuentemente se toman elementos del conjunto de los números reales ℛ. A estas funciones se les llama funciones de variable real y la regla de correspondencia es una fórmula.
El dominio de la función consiste en todos los elementos del conjunto de partida, mientras que el co-dominio es el conjunto de llegada. La función en sí es la regla que transforma a los elementos del dominio y devuelve los valores que toma la función, los cuales suelen formar un subconjunto del co-dominio, llamado recorrido.
Por ejemplo, sea la función:
f(x) = x2
La regla de correspondencia es x2 y la variable “x” puede tomar cualquier valor de ℛ, por lo que el dominio de la función es el conjunto de los números reales.
Ahora bien, el cuadrado de un número real es otro valor real, luego el co-dominio también es ℛ, pero el recorrido de la función, que son los valores que esta finalmente llega a tomar, es el conjunto de los reales positivos incluyendo al 0.
Funciones inyectivas: identificación y ejemplos
Una función f (x) es inyectiva siempre que no existan dos elementos de su dominio que tengan la misma imagen. En otras palabras, para cualquier par de valores a y b pertenecientes al dominio de f, debe cumplirse siempre que si f (a) = f (b), entonces a = b, por ello a la función inyectiva también se le llama función uno a uno.
Un ejemplo de función inyectiva es la función afín, aquella cuya gráfica es una línea recta. La función afín tiene la forma f(x) = mx + c, por lo que f(a) = m∙a + c, mientras que f(b) = m∙b + c. Igualando f (a) y f (b), ocurre que:
m∙a + c = m∙b + c \(\Rightarrow \)a = b
Resultando que la función afín es inyectiva.
Sin embargo, la ya mencionada función f (x) = x2 no es inyectiva debido a que hay pares de elementos del dominio de la función con la misma imagen, como por ejemplo:
f (2) = 22 = 4
f (−2) = (−2)2 = 4
Existe una manera muy simple para saber si una función es inyectiva, que se conoce como el criterio de la horizontal: si sobre la gráfica de la función se traza una recta horizontal y esta corta a la curva en más de punto, entonces la función no es inyectiva. En la siguiente imagen se muestra este criterio aplicado a f(x) = x2:
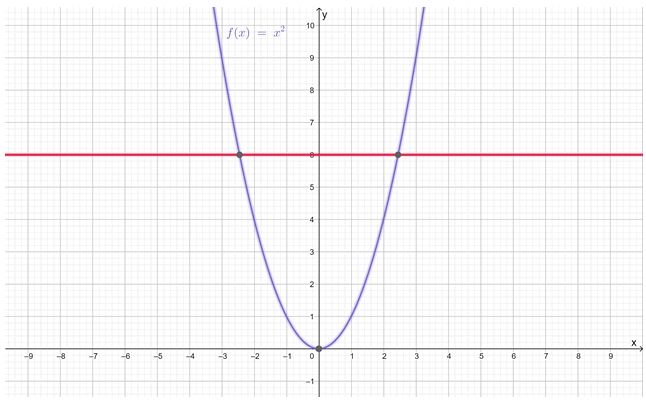
Como la recta horizontal corta a la curva en dos puntos, esta función no es inyectiva.
Funciones sobreyectivas
Este caso, es posible ilustrarlo a partir del ejemplo: para f(x) = 3x − 5, los valores de f(x) son números reales comprendidos entre − ∞ y + ∞, coincidiendo co-dominio y recorrido. Otra función sobreyectiva muy conocida es f(x) = ln x, cuyo co-dominio es el conjunto ℛ y su recorrido también es ℛ.
Por su parte, f(x) = x2 no es sobreyectiva, porque su co-dominio es el conjunto de los números reales, pero su recorrido son únicamente los reales positivos.
La forma más simple de conocer si una función es o no sobreyectiva es mirar su gráfica para observar su recorrido y comparar con el co-dominio, que usualmente se especifica al dar la función.
También se puede probar a despejar la variable “x” de f(x) y obtener así x(y), cuyo dominio de x(y) es el recorrido de y(x), pero no en todas las funciones se puede despejar “x” de forma explícita.
Ejemplo práctico 1: Funciones Sobreyectivas
Determinar si la siguiente función es inyectiva y sobreyectiva:
\(f(x)=2{{x}^{3}}-1\)
Respuesta
La función f(x) es polinómica, por lo tanto su dominio es el conjunto ℛ y su co-dominio también. Es inyectiva, puesto que al hacer:
\(f(a)=2{{a}^{3}}-1\)
Y
\(f(b)=2{{b}^{3}}-1\)
Se cumple que si f(a) = f (b), entonces:
\(f(a)=f(b)\Rightarrow 2{{a}^{3}}-1=2{{b}^{3}}-1\)
Y de esta manera a = b, por lo que la función es inyectiva.
Para averiguar si la función es sobreyectiva, se despeja x de f(x) y se obtiene:
\(x=\sqrt[3]{\frac{y+1}{2}}\)
El dominio de x (y) es ℛ, por lo tanto, el recorrido de y (x) también es ℛ e igual al co-dominio de la función, siendo esta sobreyectiva. Esto se aprecia mejor en la gráfica de f(x):
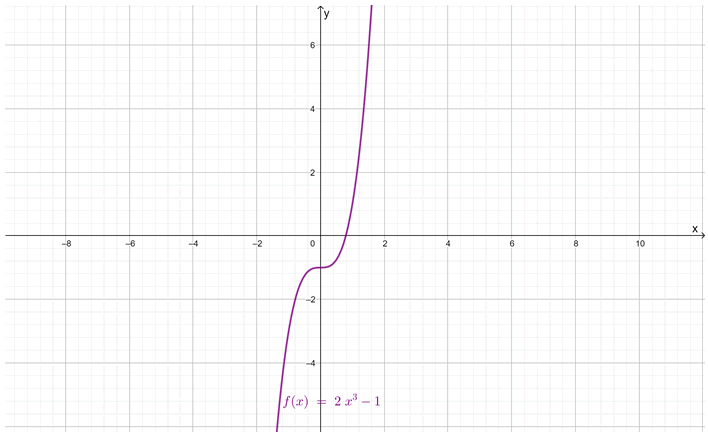
Funciones biyectivas
Las funciones biyectivas son inyectivas y sobreyectivas simultáneamente. Entre las funciones ya mencionadas, f(x) = 3x − 5 es biyectiva, pues siendo de la forma f(x) = mx + c es inyectiva, y en el apartado anterior se verificó que a la vez es sobreyectiva.
Evidentemente f(x) = x2 no es biyectiva, pues no es inyectiva ni sobreyectiva, a menos que se redefina su dominio. Por ejemplo, si se define el dominio de f(x) = x2 como ℛ+, es decir, el conjunto de los reales positivos, entonces la función pasa a ser inyectiva y sobreyectiva, por lo cual automáticamente es biyectiva.
Las funciones biyectivas tienen la ventaja de poseer inversa. La inversa de una función f es otra función f−1, tal que si f(a) = b, entonces f−1 (b) = a.
Al efectuar la composición de una función con su inversa, el resultado es f(x) = x, que es la función identidad. Y al momento de graficar f y f−1, resulta que las curvas obtenidas son simétricas con respecto a la recta y = x.
Por ejemplo, la función f(x) = ln x es sobreyectiva e inyectiva, pues el valor de y = ln x es único, luego f(x) = ln x es biyectiva y posee una inversa, que es la función exponencial f−1 = ex.
En general, para conocer la inversa de una función se verifica primero si esta es biyectiva y después se procede a despejar la variable “x”. Luego se intercambia de nombre la x con la y y el resultado es la inversa buscada.
Ejemplo práctico 2: Funciones biyectivas
Hallar la inversa de la función:
\(f(x)=2{{x}^{3}}-1\)
Respuesta
En el ejemplo resuelto 1 se determinó que esta función es inyectiva y sobreyectiva, por lo tanto es biyectiva y efectivamente tiene inversa. Primero se determina x(y):
\(x=\sqrt[3]{\frac{y+1}{2}}\)
Ahora se cambia la “y” por la “x” para obtener la inversa buscada:
\({{f}^{-1}}(x)=\sqrt[3]{\frac{x+1}{2}}\)
La siguiente gráfica muestra la curva f(x) en morado, la de su inversa, denotada como g(x) en verde y la recta y = x en rojo, que actúa como eje de simetría para ambas curvas.


Trabajo publicado en: Mar., 2021.