¿Qué es la Jerarquía de Operaciones?

Ángel Zamora Ramírez
Licenciado en Física

La jerarquía de operaciones es una convención matemática que establece el orden en que deben realizarse acciones de cálculo combinadas en un mismo enunciado matemático, es decir, cuando se tiene un enunciado matemático en donde existen operaciones matemáticas (suma, resta, multiplicación, división, potencias y raíces) combinadas, estas tienen que realizarse en un orden específico para llegar a un resultado común.

Pero, ¿por qué se necesita una jerarquía? Para poder responderlo, primero tenemos que entender bien la naturaleza de las operaciones matemáticas, que consiste en una transformación que se aplica sobre los elementos de un conjunto. Pensemos, por ejemplo, en el conjunto de los números reales, es decir, esos números que todos conocemos. Si tomamos un número a y lo sumamos con otro número b obtendremos otro número c que pertenece al mismo conjunto de los reales, es decir:

a+b = c

En la suma el orden en el que se presentan los sumandos no afecta el resultado final, es decir, que a+b = b+a, esta propiedad se denomina conmutatividad. Es importante hablar de la suma porque es la operación básica de la cual se desprenden todas las demás. Una multiplicación no es más que una serie de sumas repetidas. Si nosotros tenemos de nuevo un número a y lo multiplicamos por un número b lo que estamos haciendo es sumar a veces el número b consigo mismo, o bien, sumar b veces el número a consigo mismo. Esto último es así ya que la multiplicación es conmutativa al igual que la suma, esto implica que: a⋅b = b⋅a. Lo mencionado anteriormente puede expresarse como:

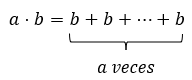
Podemos visualizar fácilmente esto con un ejemplo. Realicemos la multiplicación 5×2:

5×2 = 2×5 = 2+2+2+2+2 = 5+5 = 10

Ahora, ¿qué pasa si tenemos que realizar una operación en la que tenemos combinada suma con multiplicación? Por ejemplo: a⋅b+c. ¿Cuál es el orden en el que se tiene que realizar la suma y la multiplicación? ¿A qué operación tenemos que darle preferencia? Si realizamos primero la multiplicación y la desarrollamos como una suma tendríamos:

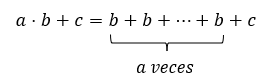
Ahora, si realizáramos primero la suma y luego la multiplicación se obtendría:

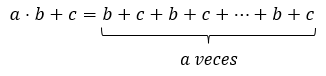
Como la suma es conmutativa podemos reagrupar el lado derecho de la ecuación para tener:

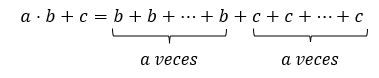
Comparando los resultados obtenidos en ambas situaciones es fácil darnos cuenta que:

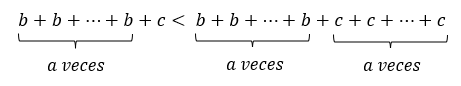
Concluimos entonces que el orden en el que se decida realizar las operaciones afecta el resultado obtenido. Lo mismo sucede cuando involucramos potencias. Cuando elevamos un número b a una potencia c lo que estamos haciendo es multiplicar c veces el número b consigo mismo, es decir:

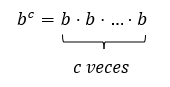
Procedemos ahora a realizar la siguiente operación combinada que involucra multiplicación y potencia a⋅b^c en diferente orden como lo hicimos en el caso anterior. Si primero le damos prioridad a la potencia tenemos:

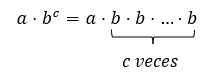
Ahora, si realizamos primero la multiplicación y luego la potencia se tendría:

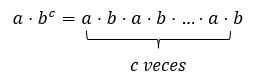
Aprovechando la conmutatividad de la multiplicación podemos reagrupar el lado derecho de la ecuación como:

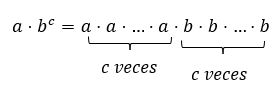
De nuevo, podemos comparar los resultados obtenidos al realizar las operaciones en distinto orden para darnos cuenta que:

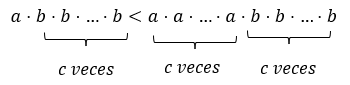
También en este caso el orden en el que se realizan las operaciones afecta al resultado obtenido. Entonces, ¿Cuál es el orden en el que se tienen que realizar las operaciones? La jerarquía de operaciones establece que las potencias están en un nivel de jerarquía mayor al de las multiplicaciones, de tal manera que las potencias tienen preferencia en un enunciado matemático. A su vez las multiplicaciones tienen un nivel de jerarquía mayor al de las sumas.

Pero, ¿Qué sucede con las restas, las divisiones y las raíces? La resta es la operación opuesta a la suma, cuando nosotros a un número a le restamos un número b obtenemos otro número c tal que c+b=a. Con la división y la resta pasa algo parecido. Si un número a lo dividimos entre un número b y nos da como resultado un número c, hemos encontrado un número tal que b⋅c=a. Y finalmente, al calcular la raíz b de un número a encontramos un número c tal que c^b=a. Estas equivalencias hacen que la resta, la división y la raíz estén en el mismo nivel de jerarquía que la suma, la multiplicación y la potencia, respectivamente.

Prácticas de paréntesis y corchetes

Ahora, ¿Qué pasa si queremos darle prioridad a unas operaciones en un enunciado matemático independientemente de su nivel de jerarquía? Para ello se hace uso de los paréntesis y los corchetes. Supongamos que tenemos el enunciado del principio a⋅b+c. Con lo que hemos dicho anteriormente ya sabemos que tenemos que realizar primero la multiplicación y luego la suma. Pero, ¿Y si quisiéramos que esto no fuera así? Para ello tendríamos que usar paréntesis o corchetes para separar la suma de la multiplicación y así darle prioridad a calcular primero la suma, es decir: a⋅(b+c). Esto hace que los enunciados separados por paréntesis y corchetes tengan la máxima prioridad por encima del resto de operaciones.

Con todo lo dicho anteriormente, la jerarquía de operaciones, o el orden en el que deben de efectuarse, es el siguiente:

1) Paréntesis y corchetes
2) Potencias y raíces
3) Multiplicaciones y divisiones
4) Sumas y restas

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Ene., 2023.

Datos para citar en modelo APA: Zamora Ramírez, A. (enero, 2023). Definición de Jerarquía de Operaciones. Significado.com. Desde https://significado.com/jerarquia-operaciones/