Definición de Números Enteros

Ingeniera Industrial, MSc en Física, y EdD
Los números enteros es la agrupación matemática que engloba las expresiones naturales positivas, negativas y el cero, pero sin incluir las fracciones. Se denotan por la letra \(\mathbb{Z}\), dado por los enteros positivos como \(\mathbb{Z}\) +, los enteros negativos como \(\mathbb{Z}\) –, por su parte, el cero se considera neutral, es decir no tiene signo. Si se emplea la notación de conjunto, estos números se pueden expresar como:
\(\mathbb{Z}\): {…., -3, -2, -1, 0, 1, 2, 3, …}
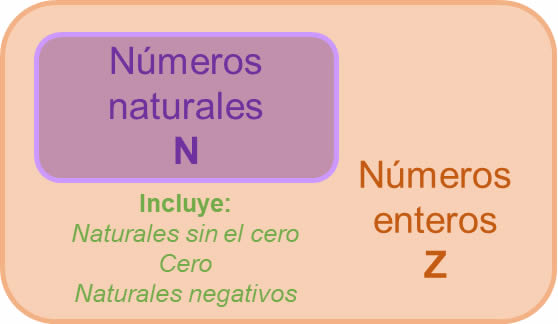
Los enteros negativos siempre llevan un signo menos (-) delante, mientras que los positivos, aunque su representación puede contener un signo más (+), se sobreentiende que son positivos si no llevan ningún signo. En general, este conjunto numérico se usó para poder expresar cantidades negativas, y ahora es comúnmente utilizado en muchas ramas de la matemática y la ciencia.
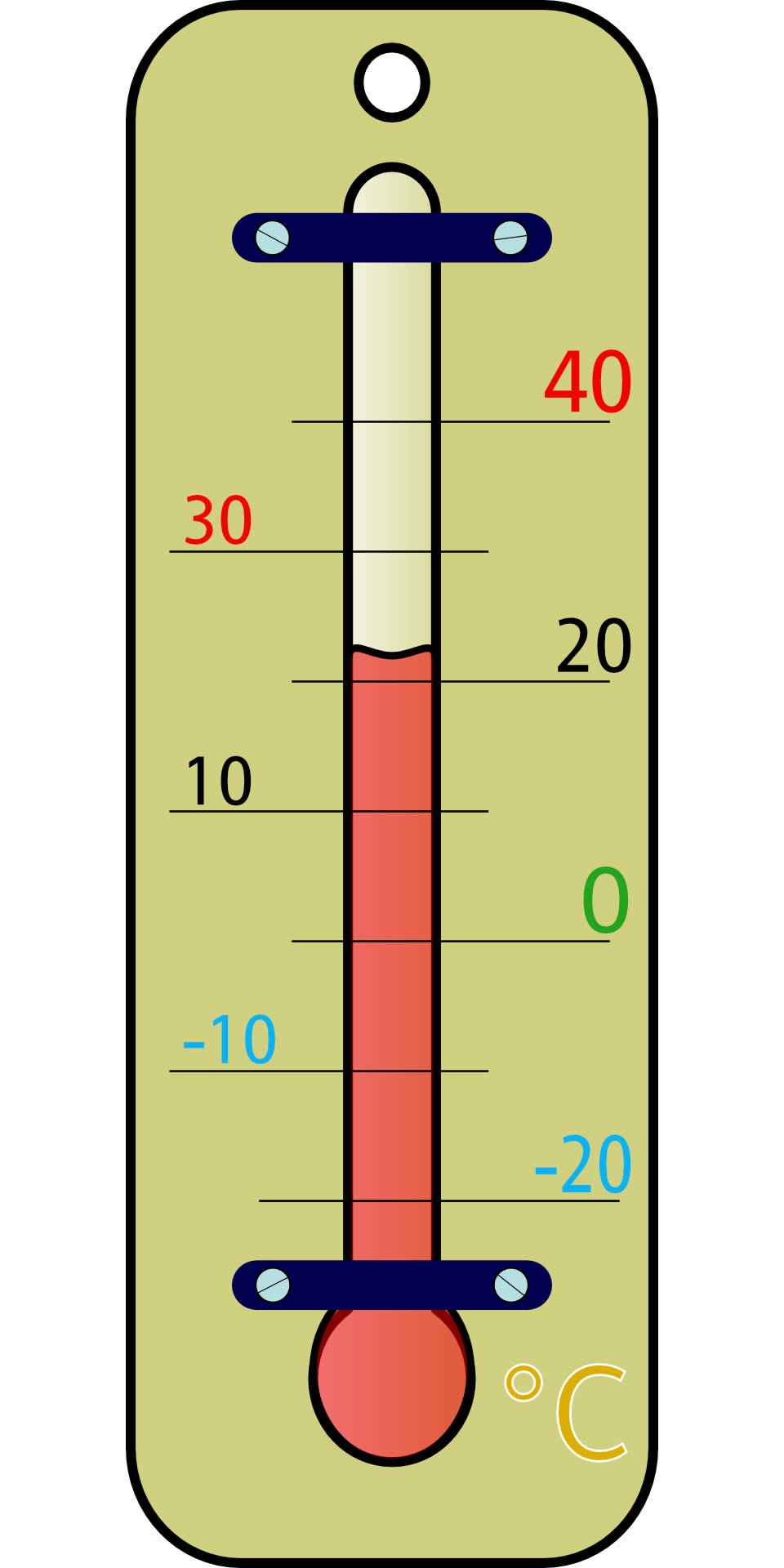
Algunas magnitudes físicas requieren del uso de números negativos para expresarlas correctamente. Un ejemplo de esto es la temperatura, la cual, en el termómetro de la imagen se mide en grados Celsius (°C) y tiene como referencia el punto de congelación del agua, que equivale a 0 °C. Por debajo de este valor, se considera que la temperatura es negativa y se requiere de números negativos para poder representarla.
El conjunto de números enteros se creó para poder expresar cantidades negativas, y se comenzaron a utilizar desde el siglo XV. Sin embargo, fue en 1770 cuando Leonardo Euler justificó su uso y posteriormente estos números fueron legítimamente aceptados. De esta manera, se creó un conjunto más completo que los números naturales, los cuales incluyen los números negativos. Es interesante mencionar que en la antigüedad, los números negativos se consideraban no naturales o absurdos y se les denominaba números deudos o números falsos.
Características y reglas de los signos
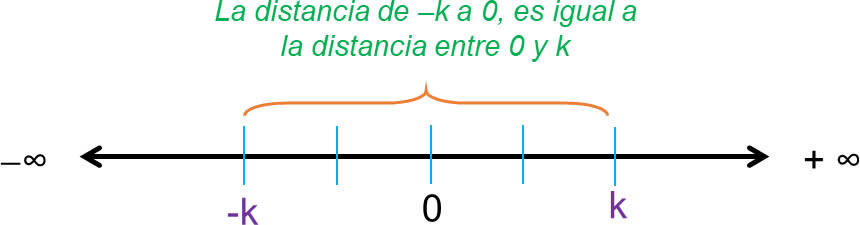
• La distancia que hay del 0 a un número, por ejemplo, +k, es la misma que hay desde 0 hasta el opuesto de ese número –k, es decir, que ambos tienen la misma magnitud o valor absoluto, que sería k.
• Las operaciones básicas con los enteros son la suma, la resta, la multiplicación y la división, y estas operaciones tienen ciertas propiedades y características especiales en este conjunto numérico. En este sentido, existen dos reglas relacionada con los signos para realizar estas operaciones: regla de los signos para adición y sustracción, y regla de los signos para multiplicación y división.
Regla de los signos para adición y sustracción
• Si las cantidades a sumar o restar tienen signos iguales, dichos números se suman y se coloca el mismo signo, por ejemplo:
-4 -7 = -11
Debido a que tanto el 4 como el 7 tienen el mismo signo (-), el resultado será la suma de 4 + 7, pero con el signo que tenían ambos números, es decir, -11.
• Cuando los números tienen signos diferentes, las cantidades se restan y el resultado quedará con el signo del valor mayor. Por ejemplo:
15 – 21 = -6
Puesto que los números de la operación tienen distinto signo (+ y -), el resultado se determina restando ambas cantidades y colocándole el signo del mayor, en el ejemplo sería la diferencia entre 15 y 21, y como el mayor es el 21 y tiene signo negativo, sería -6.
Regla de los signos para multiplicación y división
A diferencia de la regla anterior, en este caso, se aplica cuando la operación a resolver es de un producto o división de factores. La siguiente tabla muestra los criterios:
| Signo | Operación | Signo | Igual | Resultado | Ejemplo |
|---|---|---|---|---|---|
| + | x ó ÷ | + | = | + | 11 x 3 = 33 |
| + | x ó ÷ | – | = | – | 10 ÷ -5 = -2 |
| – | x ó ÷ | + | = | – | -7 x 8 = -56 |
| – | x ó ÷ | – | = | + | -6 ÷ -2 = 3 |

Las reglas de los signos establecen los criterios para efectuar las operaciones básicas de suma, resta, multiplicación y división entre números.
Ejemplo de operaciones con números enteros
Determinar el resultado de la siguiente expresión:
-10(-8) – 3(7) + 9÷3
En primer lugar, se identifican los términos de la expresión, es decir, las operaciones de suma y resta. En cada término puede haber operaciones de multiplicación o división que hay que resolver primero antes de las sumas o restas de términos. En el ejemplo, los términos serían:
• Término 1: -10(-8) ⟶ se aplica la regla del producto – x – = +
• Término 2: -3(7) ⟶ se aplica la regla del producto – x + = –
• Término 3: 9÷3 ⟶ se aplica la regla de la división + ÷ + = +
Resolviendo cada término, resulta:
80 – 21 + 3
Luego, se resuelven las operaciones de suma y resta entre los términos, dando como resultado:
-10(-8) -3(7) + 9÷3 = 62

Los números enteros permiten realizar operaciones que arrojen como resultado cantidades negativas sin decimales, por lo cual tienen un mayor alcance que los números naturales.
Aplicaciones
Los enteros tienen muchas aplicaciones prácticas en la vida cotidiana y en diversas ramas de la ciencia y las matemáticas. Entre las aplicaciones más comunes se encuentran:
• Coordenadas en un plano cartesianos
• Temperatura y cambios de temperatura
• Velocidad y aceleración
• Altura y profundidad en un sistema de referencia
• Suma y resta de valores económicos, como ingresos y deudas
• Ejecución de operaciones matemáticas y de programación
• Representación de valores en sistemas de bases numéricas, como el binario y el hexadecimal
En conclusión, los enteros son fundamentales en muchas aplicaciones prácticas y en la ciencia y las matemáticas en general.

Art. actualizado: Abril 2023; sobre el original de abril, 2011.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.