Definición de Números Naturales
1. Todos los números enteros y positivos que forman parte del sistema numérico. Dependiendo del campo matemático, puede comenzar en cero N = {0, 1, 2, 3, ...} o 1 N = {1, 2, 3, 4, ...} y, ambos casos, continuar infinitamente.
Etimología: Número, por el latín numĕrus, con raíces en las lenguas indoeuropeas como nommer, conjugado sobre *nem-, *nom-, en cuanto ‘asignar’, ‘ordenar’, y el sufijo -eso. + Natural, por el latín naturālis, respecto de natum, por ‘nacido’, como participio del verbo nascĕre, por ‘nacer’, seguido de los sufijos -ūra, que atribuye ‘calidad’, y -lis, como ‘modo asociativo’.
Cat. gramatical: Sustantivo masc.
En sílabas: nú-me-ro/s na-tu-ral/-ra-les.
Números Naturales
Ingeniera Industrial, MSc en Física, y EdD
Los números naturales son un subconjunto de los números enteros (y por ende de los reales y los complejos). Este conjunto abarca aquellos números que se emplean para contar, es decir, valores enteros y positivos (la mayoría de los autores no incluyen al cero). A todo número natural le corresponde un número sucesor inmediato.
La cantidad de alumnos en un salón de clases se representa con un número natural.
Al conjunto formado por los números naturales se denota con el símbolo N, y está formado por infinitos miembros, ya que la cantidad de números con los que se puede contar es interminable:
N = { 1,2,3,4,5, … }
Los números naturales no solo sirven para contar, ya que con ellos también se pueden efectuar muchas operaciones matemáticas, como adición, sustracción, multiplicación, división, potenciación y hasta aplicar otros operadores como derivadas e integrales.
La suma o producto de dos números naturales, da como resultado otro número natural.
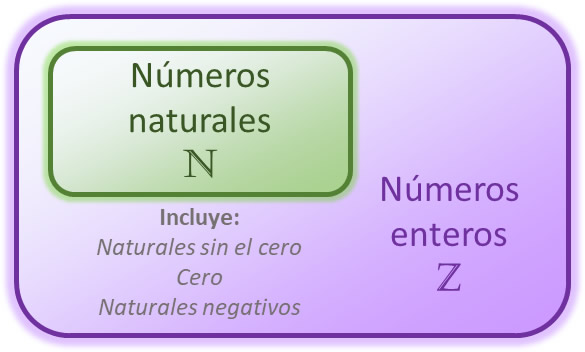
Los números naturales son un subconjunto de los números enteros.
Representación de los números naturales en la recta real
Los números naturales se enmarcan dentro de un sistema de numeración decimal posicional, lo que implica que cada dígito dentro de un número está asociado a un valor, de esta manera, al analizar un número de ocho cifras (por ejemplo, 23,627,497), éste se conforma de 2 decenas de millón, 3 unidades de millón, 6 centenas de mil, 2 decenas de mil, 7 unidades de mil, 4 centenas, 9 decenas y 7 unidades:
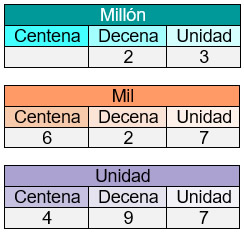
Ahora bien, si se desea representar un número natural en la recta numérica, se debe empezar trazando una recta horizontal y se designa de manera arbitraria un origen donde se ubicará el cero (se recomienda localizarlo al extremo izquierdo).
El siguiente paso consiste en trazar de forma equidistante pequeños segmentos de recta vertical sobre la línea horizontal, para representar a cada número natural. Hay que tener en cuenta que se debe seleccionar una separación apropiada entre segmentos para que la cantidad a ubicar en la recta pueda representarse; por ejemplo, si el número a ubicar en la recta es el 5, se debe asegurar que en dicha recta quepan al menos seis segmentos:
En caso de que las cantidades sean muy elevadas, por ejemplo, 250. Se puede optar por utilizar escalas que permitan la representación de dicho número. Una opción puede ser, considerar que cada división equivale a 50 unidades:
Números primos y compuestos
Los números naturales puede descomponerse y clasificarse considerando sus divisores, de manera que se tienen los números naturales que solo se pueden dividir de forma exacta entre ellos mismos y entre la unidad (1), y se conocen como números primos; y por el contrario, aquellos que tienen más de dos divisores, a los que se les llaman números compuestos.
Para identificar si una cantidad tiene más de dos divisores, es importante recordar que los divisores permiten, valga la redundancia, la división de otro número en partes exactas, por lo que en esta clase de operación, el resto siempre es cero. Por ejemplo, se sabe que el número 3 es divisor de 18, ya que si dividimos 18 entre 3, el resultado es 6 con exactitud, y el resto o residuo de la división es cero.
Es de gran ayuda al momento de identificar los divisores de algunos números el conocer ciertas reglas o criterios básicos de divisibilidad. Algunas de estas reglas son:
– Todo número par es divisible entre 2.
– Todo número que termine en 5 o 0, es divisible entre 5.
– Todo número que termine en 0, es divisible entre 10.
– Si la suma de los dígitos de un número es múltiplo de 3, entonces el número completo es divisible entre 3.
Con estas consideraciones, se puede deducir que casi todos los números naturales del 1 al 100 son números compuestos, excepto los números que se muestran en la siguiente tabla:
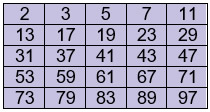
Ejercicio con números naturales a modo de ejemplo
En una cancha de un colegio se reunirán los alumnos de 5 salones de clases. Cada salón tiene la siguiente cantidad de alumnos:
Salón A: 23 alumnos
Salón B: 17 alumnos
Salón C: 25 alumnos
Salón D: 20 alumnos
Salón E: 21 alumnos
¿Cuántos alumnos se reunirán en la cancha?
Para responder la pregunta planteada, simplemente se debe sumar la cantidad de alumnos en cada salón. La cantidad de personas representa un número natural, por lo tanto, la suma de cantidades de personas, también será un número natural:
Cantidad de alumnos en la cancha = 23 + 17 + 25 + 20 + 21 = 106 alumnos
Art. actualizado: Enero 2023; sobre el original de diciembre, 2013.