Significado de límites (en matemática) Definición, propiedades, y funciones

Doctor en Ingeniería
Definición formal
Matemáticamente, una sucesión \([x_n]_{n\geq 1}\) tiene un límite L si y sólo si para todo Ε mayor que 0 existe N tal que si \(n\geq N\), por lo tanto, \(\text{dist}(x_n,L)<\epsilon\).
Supongamos que arrojamos una bolita dentro de una superficie cóncava (un wok, por ejemplo). La bolita seguramente rodará por los bordes, oscilando un poco, y acercándose de a poco al centro hasta finalmente detenerse en el punto central. Este es el comportamiento que busca reflejarse y explicarse.
Más formalmente, consideremos una sucesión infinita \([x_1, x_2, x_3, \ldots]\), con \(x_n \in \mathbb{R}^2\), que tiene un límite \(L\in \mathbb{R}^2\). Sin definir todavía la noción de límite, sino más bien pensando en el ejemplo anterior, intuitivamente podríamos esperar que, a medida que avanzamos en la sucesión, los elementos estén cada vez más cerca del límite, como se observa en la figura 1.
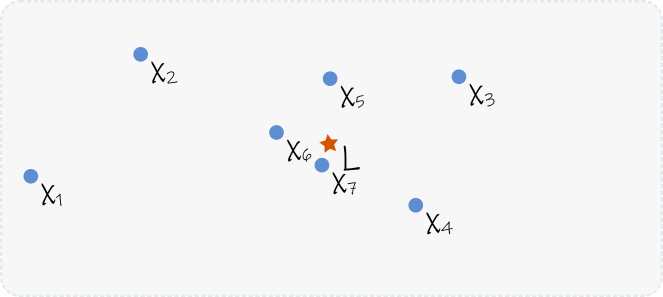
¿Entonces si una sucesión tiene un límite L, sus elementos xn están cada vez más cerca de L? Casi. Si pensamos en el primer ejemplo intuitivo, la bolita podía pasar cerca del centro del wok, alejarse y luego acercarse al centro de nuevo. Lo que ocurre es que después de un tiempo, la bolita va a oscilar sin acercarse al borde, y después de un tiempo más, va a oscilar cerca del centro, cada vez en un entorno más pequeño.
En nuestra sucesión, esto es análogo a pensar que si dibujamos un círculo de radio Ε al rededor del límite L, a partir de cierto valor de n, todos los elementos sucesivos van a quedar dentro del círculo. Y más aún, si dibujamos un círculo con radio Ε más chico, debería haber también cierto valor de n mayor a partir del cual todos los elementos de la sucesión queden comprendidos dentro. Esto nos lleva a la definición formal de límite para una sucesión.
Una sucesión \([x_n]_{n\geq 1}\) tiene un límite L si y sólo si para todo Ε > 0 existe N tal que si \(n\geq N\), entonces \(\text{dist}(x_n,L)<\epsilon\).

Propiedades de los límites
En la expresión matemática se observa la noción de distancia, lo que quiere decir que esta definición no sólo vale para sucesiones definidas en \(\mathbb{R}^M\), sino para cualquier espacio donde pueda definirse una distancia. Si nuestras sucesiones están definidas en \(\mathbb{R}^M\), pueden deducirse varias propiedades del límite. Entre ellas:
1. Una sucesión puede tener un único límite.
2. La suma de los límites es el límite de la suma: \(\lim_{n\rightarrow \infty}[x_n] + \lim_{n\rightarrow \infty}[y_n] = \lim_{n\rightarrow \infty}[x_n+y_n]\).
3. Toda sucesión acotada tiene una subsucesión convergente.
Cabe destacar que las propiedades 1 y 2 valen para cualquier espacio métrico, mientras que la propiedad 3 requiere de hipótesis adicionales, por lo que no tiene sentido tratar de listarlas todas. Sigamos, en cambio, viendo cómo nuestra definición de límite puede aplicarse al concepto de funciones.
Límites de funciones
Consideremos (por simplicidad) una función \(f:\mathbb{R}\rightarrow\mathbb{R}\) alrededor del punto x0. Para construir una analogía con el concepto de límite en sucesiones, podemos decir que el límite de f(x) cuando x tiende (se acerca) a x0 es L si a medida que x se acerca a x0, f(x) se acerca a L. Dado que en este punto no tenemos un valor n que nos indique que avanzamos en la sucesión, nos fijamos en cambio en la distancia entre x y x0. Formalmente, \(\lim_{x\rightarrow x_0}f(x) = L\) si y sólo sí para todo Ε > 0 existe Δ > 0 tal que si \(|x-x_0|<\delta\), entonces \(|f(x)-L|<\epsilon\). Gráficamente, en la Figura 3 vemos que para que L constituya el límite de f(x) en x0, dado un intervalo anaranjado \(L-\epsilon, L+\epsilon\) debemos poder encontrar un Δ > 0 de modo que si x está dentro del intervalo azul, entonces f(x) esté dentro del intervalo anaranjado, como ocurre en la Figura 3.

Esta definición permite introducir inmediatamente el concepto de continuidad. Decimos que una función f definida como antes es continua en un punto x0 si \(\lim_{x\rightarrow x_0} f(x) = f(x_0)\). Es decir, si la función f tiene un límite en x0 y este coincide con f(x0), como es el caso en la Figura 3.
Las nociones de límite y continuidad pueden aplicarse también a funciones definidas en \(\mathbb{R}^M\) u otros espacios métricos, pero de momento nos basta saber que la idea general es siempre la misma.

Trabajo publicado en: Ene., 2021.