Definición de Números Decimales

Evelyn Maitee Marín
Ingeniera Industrial, MSc en Física, y EdD

Números Decimales

Los números decimales están formados por cifras que contienen una parte entera, seguida de un punto y luego una parte decimal. Se emplean para expresar valores que se encuentran entre dos números enteros consecutivos.

Entre dos números enteros, se ubican infinitos números decimales que se pueden representar en una recta numérica.

Aunque no existe una fecha precisa de invención de los números decimales, los registros de sus primeros usos en occidente se le atribuyen a Simon Stevin en 1585, quien los empleaba como una opción al uso de las fracciones. Sin embargo, la forma de expresar los números decimales en ese entonces, difiere respecto a la actual, por ejemplo, para representar el número 0.0796; lo indicaba de esta manera:

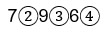
que se lee: 7 segundas, 9 terceras, 6 cuartas.

La nomenclatura que se utiliza en la actualidad fue propuesta por Jhon Napier, en la cual se utiliza un punto decimal (o una coma), para los números decimales, de la misma manera como se emplea en la actualidad.

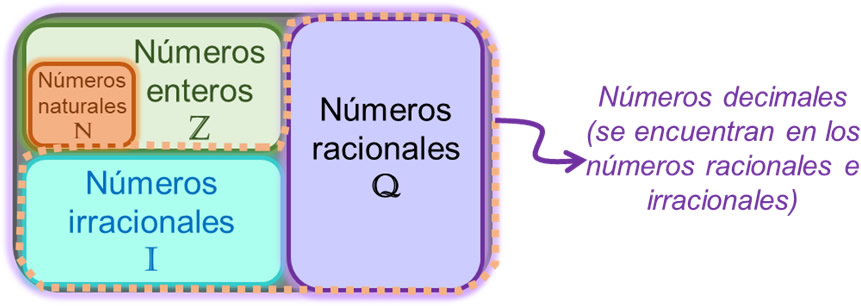
Los números decimales pertenecen al conjunto de los números racionales (Q) y de los números irracionales (I)

Valor posicional

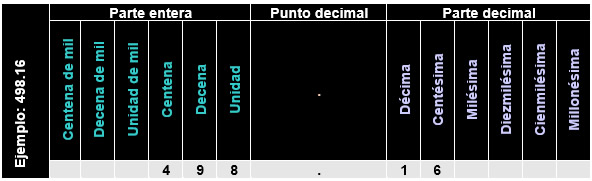
El valor posicional se relaciona con la ubicación que ocupa cada dígito en un número. En particular, los números decimales obedecen a dos tipos de posiciones: una para la parte entera, y otra para la parte decimal, ya que están representados de la siguiente forma:

Como se observa, el punto en un número decimal, es el símbolo que separa la parte entera (a la izquierda) de la parte decimal (lado derecho)

Ahora bien, en función de la ubicación que ocupe cada dígito en la cifra, se le asocia un valor posicional considerando las siguientes categorías:

Tipos de números decimales

Los decimales exactos: esta denominación se emplea para referirse a las cifras decimales conformadas por una cantidad finita o limitada de dígitos, por ejemplo:

– 1,907 (contiene decimales hasta la milésima)
– 158621,03348 (contiene decimales hasta la cienmilésima)
– 847,9 (contiene decimales hasta la décima)

Números periódicos: a diferencia de los decimales exactos, en esta categoría se encuentran las cifras decimales que tienen infinitos dígitos en su parte decimal y esta exhibe un patrón que se repite. Los números periódicos se pueden clasificar a su vez en:

Periódicos puros: estos números tiene una parte decimal que se repite inmediatamente después del punto decimal. Por convención, en el patrón de la cifra decimal se le suele colocar un arco en la parte superior, así por ejemplo, el número 1.33333333…, se puede expresar:

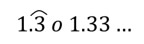
Periódicos mixtos: estos números poseen en su parte decimal uno o más dígitos que preceden a los números periódicos, por lo que a los números de la cifra decimal que preceden al periodo se denominan ante – periodo, por ejemplo, en el número 36.07999999…, se puede identificar:

No exactos ni periódicos

Estos números decimales poseen infinitos dígitos no periódicos en su parte decimal, y se les conoce también como números irracionales; es decir, no tienen patrones en la parte decimal la cual contiene infinitos dígitos, por ejemplo:

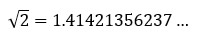
El resultado de π (pi), representa un número decimal, puesto que contiene infinitos dígitos no periódicos en su parte decimal, por ello, pertenece al conjunto de los números irracionales. El valor de π es una constante que se determina al dividir el perímetro de cualquier circunferencia entre su diámetro. En muchos contextos su parte decimal se aproxima hasta la centésima π = 3.14

Transformación de un número decimal en una fracción

Cualquier número decimal exacto o periódico, se puede convertir en una fracción equivalente. El procedimiento para dicha transformación es:

Para números decimales exactos, se emplean potencias de base 10, para lo cual se escribe en el denominador un 1 seguido de tantos ceros como cifras decimales posea el número, por ejemplo:

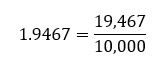
Para números decimales periódicos puros, se debe escribir el número sin el punto decimal, y luego se resta el o los números que se encuentren antes del periodo. A este resultado se le coloca de denominador un 9 por cada dígito que se encuentre antes del periodo, por ejemplo:

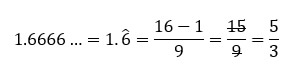
Para números decimales periódicos mixtos, el numerador representa la resta del número omitiendo el punto decimal menos todo lo que se encuentra antes del periodo. En el denominador, se colocan tantos 9 como dígitos tenga el periodo, seguido de tantos 0 como dígitos contenga el ante-periodo, por ejemplo:

Por: Evelyn Maitee Marín. Ingeniera industrial con maestría en Ciencias aplicadas de Física y doctorado en Ciencias de la Educación. Profesora de la Universidad del Zulia.

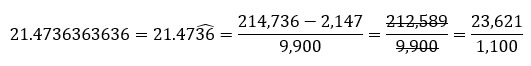
Art. actualizado: Feb. 2023; sobre el original de abril, 2011.

Datos para citar en modelo APA: Marín, E. M. (Feb. 2023). Definición de Números Decimales. Significado.com. Desde https://significado.com/numeros-decimales/