Significado de números reales Definición, clasificación, y propiedades

Doctor en Ingeniería
Definición formal
Un número real es un valor que puede cuantificar cualquier distancia entre dos puntos reconocidos sobre una recta.
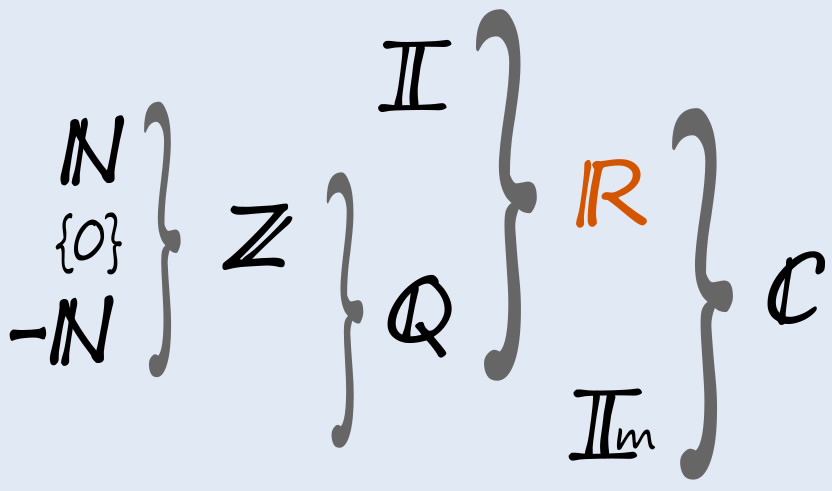
Básicamente, dado un punto en la recta real, no nos podemos mover mediante ninguna operación numérica a otro punto de la recta que no sea, específicamente, un número real.
El término «reales» tiene el propósito original de distinguir a estos números de las raíces «imaginarias» de un polinomio. De este modo, los números comprendidos en \(\mathbb{R}\) agrupa el espectro de los racionales, del cual se desprenden los naturales y enteros, y por el otro lado, se identifican los irracionales, tal como lo ilustra la figura principal de la nota y como lo explicamos en las próximas líneas.
Clasificación: Naturales
El primer conjunto de números que aprendemos de pequeños, es el conjunto de los números naturales, 1, 2, 3, 4, … . Suponiendo que conocemos de antemano el concepto de suma (lo que es hacer un poco de trampa) este conjunto puede definirse como \(\mathbb{N} \doteq \{1\}\cup\{n+1,\; \forall n\in \mathbb{N}\}\). Esto quiere decir que \(\mathbb{N}\) es el conjunto que contiene al 1, y a todo elemento que se pueda obtener sumando 1 a otro elemento del conjunto.
Sobre el conjunto de los números naturales está definida entonces la suma, y puede demostrarse por inducción que si sumamos dos números naturales, obtenemos otro número natural. Pero ¿qué pasa si queremos resolver la siguiente ecuación?
x + 2 = 1
Clasificación: Enteros
La ecuación anterior no tiene solución en los números naturales, y es por eso que agregamos los números negativos y el cero para formar los números enteros \(\mathbb{Z} \doteq \mathbb{N}\cup\{0\}\cup\{-n,\; \forall n\in\mathbb{N}\} = \{\ldots -3, -2, -1, 0, 1, 2, 3, \ldots\}\). Ahora podemos restar tranquilos, que siempre nos vamos a mantener dentro de \(\mathbb{Z}\).
Pero nos gustaría definir también el producto. Y si bien es cierto que el producto de dos números enteros da como resultado un número entero, nos encontramos con que la ecuación
2x = 3
no tiene solución en \(\mathbb{Z}\).
Clasificación: Racionales
Entonces, es hora de volver a ampliar nuestro conjunto, y definir los números racionales \(\mathbb{Q} \doteq \{\frac{p}{q}, \,\forall p, q\in\mathbb{Z}, q\neq 0\}\). Es decir, todos los números que pueden escribirse como cociente de dos números enteros.
Pero todavía falta la potenciación. Y cuando nos damos cuenta de que la ecuación
x2 = 2
no tiene solución en \(\mathbb{Q}\), es que nos damos cuenta de que tiene que haber algo más: los números irracionales \(\mathbb{I}\), que junto a \(\mathbb{Q}\) conforman los números reales.
Propiedades de los Números Reales
Las propiedades básicas de los números reales son las siguientes:
1. \(\mathbb{R}\) es un conjunto ordenado, por lo que dados \(x, y, z \in \mathbb{R}\) cualesquiera, se cumplen:
A) Reflexividad: \(x\leq x\) .
B) Transitividad: Si \(x\leq y\) y \(y\leq z\), entonces \(x\leq z\) .
C) Antisimetría: Si \(x\leq y\) y \(y\leq x\) entonces x=y .
D) Completitud: \(x\leq y\) o \(y\leq x\) .
2. La suma y el producto son cerrados. Es decir, siempre \(x+y\in\mathbb{R}\) , \(xy\in\mathbb{R}\) .
3. Potencia del Continuo: No se puede establecer una biyección entre los números reales y los naturales. En otras palabras, no se puede hacer una lista infinita con todos los números reales: son «más infinitos» que los naturales.
4. \(\mathbb{R}\) es completo como espacio métrico: Es decir que toda sucesión de Cauchy (sucesión cuyos elementos están cada vez más cerca) converge a un límite.
\end{enumerate}
Números complejos
Así como vimos que la imposibilidad de resolver 2x = 3 en \(\mathbb{Z}\) justifica la creación de \(\mathbb{Q}\), existe otro conjunto de números más grande, que contiene a \(\mathbb{R}\) y permite resolver
x2 = -2
Se llaman números complejos, \(\mathbb{C}\), e incorporan la unidad imaginaria i, que cumple i2 = -1. Estos números tienen la forma \(x+iy\), \(x, y \in\mathbb{R}\), y ya no se ubican en la recta, sino en el plano, donde la primera coordenada representa la componente real x, y la segunda coordenada la componente imaginaria y.

Trabajo publicado en: Feb., 2021.