Definición de Oscilación

Ángel Zamora Ramírez
Licenciado en Física

Una oscilación es un fenómeno en el que un sistema presenta un movimiento periódico o repetitivo en torno a una posición de equilibrio.

Las oscilaciones forman parte de nuestra vida cotidiana. Cuando hay un sismo, las ondas sísmicas que llegan a la superficie crean oscilaciones en las construcciones; muchos parámetros financieros presentan comportamientos oscilatorios; el constante movimiento de nuestro planeta entorno a su eje de rotación puede considerarse un movimiento oscilatorio e incluso muchos aspectos del mundo cuántico pueden ser descritos en términos de oscilaciones y ondas.

Generalmente, se habla de oscilaciones y ondas como si fueran sinónimos, pero esto no es del todo cierto. Las oscilaciones son variaciones en torno a un punto de equilibrio mientras que las ondas son perturbaciones que se propagan en el espacio. No obstante, entender cómo se describen las oscilaciones nos permite entender mejor el comportamiento de las ondas.

El oscilador harmónico simple

Consideremos el siguiente escenario: Tenemos un resorte cuyos extremos están adheridos, uno a una pared y el otro a un bloque con cierta masa \(m\). Para simplificar vamos a suponer que el bloque está sobre una superficie cuya fricción es despreciable y también vamos a ignorar otros tipos de resistencias al movimiento. Tomamos ahora el bloque y lo jalamos o empujamos para posteriormente soltarlo. El bloque comenzará a moverse hacía adelante y hacía atrás como resultado de la fuerza ejercida por el resorte la cual está dada por:
\(F = – kx\)

Donde \(F\) es la fuerza, \(k\) es una constante de proporcionalidad que representa la rigidez del resorte y \(x\) es el desplazamiento del bloque. Esto de aquí se conoce como la Ley de Hooke y describe un tipo de movimiento en el que la fuerza aplicada es directamente proporcional al desplazamiento y opuesta a este, como indica el signo menos en la ecuación anterior. Por segunda ley de Newton sabemos que \(F = ma\), por lo tanto, podemos decir que:
\(ma = – kx\)

Es decir que:
\(a = – \frac{k}{m}x\)

Donde \(a\) es la aceleración y \(m\) es la masa del bloque. Sabemos además que la aceleración es la segunda derivada del desplazamiento con respecto al tiempo, es decir que:

\(a = \frac{{{d^2}x}}{{d{t^2}}} = – \frac{k}{m}x\)

Esta es una ecuación diferencial de segundo orden, cuya solución para el desplazamiento \(x\) en función del tiempo \(t\) en este caso es:

\(x\left( t \right) = {x_m}\cos \left( {\omega t + \phi } \right)\)

Donde \({x_m}\) es el desplazamiento máximo del bloque, \(\phi \) es lo que se llama fase y está asociada con la posición inicial desde donde se soltó el bloque y \(\omega \) es la frecuencia angular que viene dada por:

\(\omega = \sqrt {\frac{k}{m}} \)

Este tipo de movimiento que experimenta el bloque se conoce como Movimiento Armónico Simple. Se trata de un tipo de movimiento oscilatorio que puede describirse con funciones periódicas simples como el seno y el coseno. El periodo del movimiento, es decir, el tiempo en el que el sistema completa una oscilación es:

\(T = \frac{{2\pi }}{\omega }\)

Muchos sistemas pueden ser descritos como osciladores armónicos simples, tal es el caso del péndulo, el cual en el límite de pequeñas oscilaciones puede aproximarse como un oscilador armónico.

Oscilador harmónico simple amortiguado

En el caso del oscilador armónico simple una suposición que hicimos desde un principio es que la fricción y otras fuerzas de resistencia eran despreciables. Esto tiene un gran impacto en los resultados finales ya que indican que el movimiento continuará repitiéndose infinitamente, lo cual está muy lejos de la realidad física.

Si nosotros hiciéramos un experimento con el caso anterior nos daríamos cuenta que eventualmente el bloque se detiene ya que existe fricción y otras fuerzas que se oponen al movimiento y que disipan energía.

Consideremos una fuerza de resistencia \({F_d}\) que es proporcional a la velocidad como ocurre con el aire y otros fluidos:

\({F_d} = – bv\)

Donde \(b\) es la constante de resistencia y \(v\) es la velocidad. La ecuación de movimiento para un oscilador armónico simple tomando en cuenta una fuerza de resistencia como la anterior sería:

\(F = ma = – kx – bv\)

Si resolvemos para obtener el desplazamiento \(x\) en función del tiempo \(t\) como en el caso anterior obtenemos lo siguiente:

\(x\left( t \right) = {x_m}{e^{ – bt/2m}}\cos \left( {\omega ‘t + \phi } \right)\)

Donde en este caso la frecuencia angular \(\omega ‘\) está dada por:

\(\omega ‘ = \sqrt {\frac{k}{m} – \frac{{{b^2}}}{{4{m^2}}}} \)

Podemos darnos cuenta que como consecuencia del factor de amortiguamiento el desplazamiento es cada vez menor conforme el tiempo avanza hasta volverse cero cuando \(t \to \infty \). Además, si despreciamos la fuerza de resistencia (\(b = 0\)) las ecuaciones anteriores se reducen al oscilador armónico simple.

Oscilaciones forzadas y resonancia

Imaginemos que una persona está en un columpio y comienza a impulsarse para ganar altura. El movimiento de un columpio es el mismo que el de un péndulo en el que un cuerpo con masa (en este caso la persona y el columpio) se mueve periódicamente de un lado a otro alcanzando una altura máxima.

Si la persona quiere seguirse columpiando o ganar más altura tendrá que usar su propio peso para impulsarse, pero esto no debe hacerlo en cualquier momento, tiene que hacerlo cuando el columpio alcanza su altura máxima.

En este caso la persona está usando su propio peso para ejercer una fuerza externa periódica cuya frecuencia es igual a la frecuencia de oscilación del columpio. Este fenómeno se conoce como resonancia y ocurre cuando se aplica una fuerza periódica sobre un sistema y la frecuencia con que se aplica dicha fuerza iguala a la frecuencia natural del sistema, es decir, la frecuencia a la que oscilaría si no hubiera fuerzas externas actuando.

El fenómeno de resonancia está presente en muchas situaciones y es un factor fundamental a considerar en la construcción y la ingeniería. En 1940 colapsó el Puente de Tacoma Narrows en Estados Unidos, se sospecha que el colapso se debió a un fenómeno de resonancia impulsado por el aire. También, algunas propiedades del subsuelo a veces favorecen que las ondas sísmicas puedan derribar construcciones debido a un fenómeno de resonancia.

Situaciones con oscilación

Además de los parámetros propios de este tipo de movimiento físico, la idea de oscilación está muy presente en la comunicación y en la vida cotidiana. Veamos tres ejemplos significativos:

– En una competición futbolística, una serie de equipos se enfrentan a lo largo de una temporada. A lo largo de la misma, su posición en la tabla va cambiando, por lo que hay una oscilación o variación en la clasificación.

– En el mundo de la bolsa los distintos valores van cambiando día a día y estas variaciones son analizadas por los entendidos, quienes observan las oscilaciones que se producen desde un punto de vista numérico y durante un periodo de tiempo.

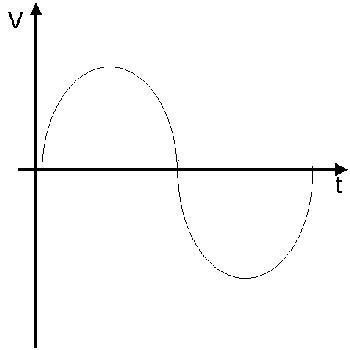
– Las ondas son el modo en que se presentan algunas de las oscilaciones. Así, el sonido, las ondas de los terremotos o las ondas de radio tienen las características propias de este movimiento.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Art. actualizado: Mayo 2023; sobre el original de abril, 2015.

Datos para citar en modelo APA: Zamora Ramírez, A. (Mayo 2023). Definición de Oscilación. Significado.com. Desde https://significado.com/oscilacion/