Significado de teorema del seno Definición, casos especiales, y ejemplos prácticos

Licenciada en Física
Definición formal
El teorema del seno determina que en todo triángulo, los lados resultan proporcionales a los senos de los ángulos cuyas ubicaciones se identifican en oposición.

Considerando el triángulo ABC mostrado en la figura, cuyos lados son “a”, “b” y “c” y con ángulos internos α, β e γ, el teorema se puede formular como
\(\frac{a}{\text{sen}~\alpha }=\frac{b}{\text{sen}~\beta }=\frac{c}{\text{sen}~\gamma }\)
O alternativamente
\(\frac{\text{sen}~\alpha }{a}=\frac{\text{sen}~\beta }{b}=\frac{\text{sen}~\gamma }{c}\)
Nótese que “a” es el lado opuesto al ángulo α, “b” es opuesto a β y “c” es opuesto a γ.
Se cree que los matemáticos musulmanes del siglo X fueron los primeros en descubrir esta relación entre los lados del triángulo y los senos de sus ángulos internos. Siglos más tarde, esta ley fue redescubierta y publicada por el matemático alemán Johannes Müller, conocido como Regiomontano (1436-1476), quien probablemente conocía los trabajos de sus predecesores árabes.
Comprobación de la fórmula
En la siguiente demostración se hace uso del teorema de Pitágoras, el cual es válido únicamente para triángulos rectángulos. Trazando la altura “h” (en amarillo en la siguiente figura), se divide el triángulo ABC en dos triángulos rectángulos: ADC y BDC. Ambos tienen el lado común “h”.
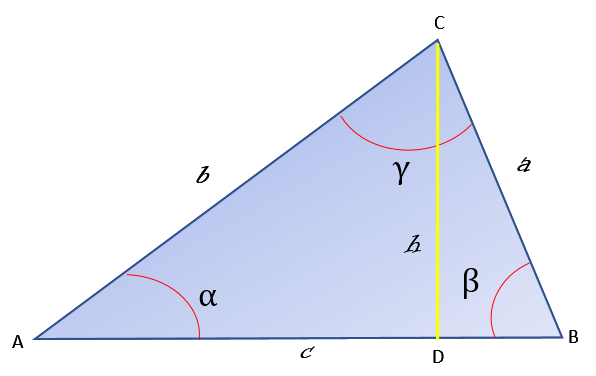
En el triángulo BDC se cumple que
\(h=a\text{sen}~\beta \)
Mientras que en el triángulo ADC, el valor de “h” se puede expresar como
\(h=b\text{sen}~\alpha \)
Procediendo a igual ambas expresiones, se obtiene
\(a\text{sen}~\beta =b\text{sen}~\alpha \)
Que se puede reescribir como
\(\frac{a}{\text{sen}~\alpha }=\frac{b}{\text{sen}~\beta }\)
Se puede trazar otra altura del triángulo, por ejemplo, sobre el lado b, para obtener
\(\frac{a}{\text{sen}~\alpha }=\frac{c}{\text{sen}~\gamma }\)
De esta manera se comprueba que
\(\frac{a}{\text{sen}~\alpha }=\frac{b}{\text{sen}~\beta }=\frac{c}{\text{sen}~\gamma }\)
Tal como se dijo al comienzo.
Requisitos necesarios para calcular
El teorema del seno se aplica para determinar un triángulo, obteniendo el valor de sus lados y ángulos internos, no obstante, se requiere que se tenga a la mano uno de estos conjuntos de datos:
• Un lado y dos ángulos, siendo uno de estos ángulos opuesto a uno de los lados conocidos.
• Dos lados y un ángulo interno opuesto a alguno de estos lados.
En este último caso hay que prestar atención a una posible ambigüedad en la respuesta, ya que con el ángulo β, podrían ocurrir las situaciones que se muestran a continuación:
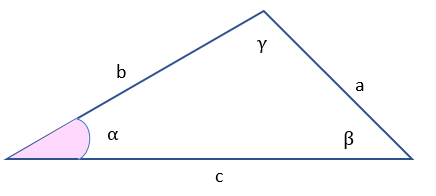
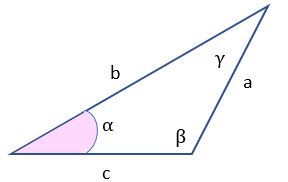
Si se conocen los lados a y b, y el ángulo opuesto al lado a, que es α y aparece resaltado en color en la imagen, el ángulo β podría ser obtuso (mayor que 90º), como en el triángulo de la izquierda, o podría ser agudo (menor que 90º), como en el de la derecha.
Esta situación de tener dos soluciones válidas para β se da cuando a < b. Las posibles soluciones se listan a continuación.
Casos especiales
Dados dos lados y un ángulo de un triángulo, siendo este ángulo opuesto a alguno de los lados, se tiene que
\(\frac{\text{sen}~\alpha }{a}=\frac{\text{sen}~\beta }{b}\)
\(\text{sen}~\beta =\frac{b\bullet sen \alpha }{a}\)
Al analizar esta fracción podrían presentarse los siguientes casos
1) b ∙ senα > a, no hay solución para el triángulo, porque la fracción sería mayor que 1, y el seno de cualquier ángulo siempre está comprendido entre -1 y 1, ambos inclusive.
2) b ∙ senα = a, entonces sen β = 1 y β = 90º, luego hay una solución única y el triángulo es rectángulo.
3) b ∙ senα < a, hay tres posibilidades, según los valores de a y b: • Una solución si a > b, resultando agudo el ángulo β.
• Si a = b, entonces sen α = sen β, por lo que α = β y el triángulo es isósceles.
• Dos soluciones si a < b, una con el ángulo β agudo y otra con el ángulo β obtuso, como se indica arriba.
Ejemplos prácticos
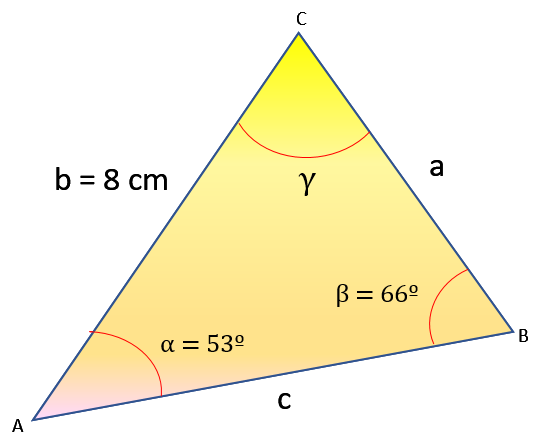
Ejemplo 1: Hallar el ángulo y los lados faltantes en el siguiente triángulo
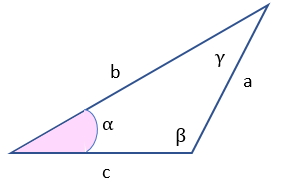
Respuesta
Los datos del enunciado son:
b = 8 cm
α = 53º
β = 66º
Como se da un lado y además dos ángulos, uno de los cuales es opuesto al lado dado, se aplica el teorema del seno:
\(\frac{\text{sen}~\alpha }{a}=\frac{\text{sen}~\beta }{b}=\frac{\text{sen}~\gamma }{c}\)
Cálculo de γ
Sabiendo que la suma de los ángulos internos de cualquier triángulo es igual a 180º, es fácil encontrar el ángulo γ:
α+β+γ = 180º
γ = 180º − 53º − 66 = 61º
No hay ambigüedad en la respuesta, puesto que dos ángulos internos del triángulo eran conocidos.
Cálculo de c
El lado c se puede calcular a partir de la igualdad:
\(\frac{b}{\text{sen}~\beta }=\frac{c}{\text{sen}~\gamma }\)
\(c= \frac{b\bullet sen \gamma }{sen \beta }=\frac{8cm\times sen 61{}^\text{o}}{sen 66{}^\text{o}}=7.66 cm\)
Cálculo de a
El lado a se calcula de:
\(\frac{a}{\text{sen}~\alpha }=\frac{c}{\text{sen}~\gamma }\)
O si se prefiere de:
\(\frac{a}{\text{sen}~\alpha }=\frac{b}{\text{sen}~\beta }\)
Sustituyendo en la primera de estas expresiones:
\(a=\frac{cosen~\alpha }{sen~\gamma }=\frac{7.66cm\times sen~53{}^\text{o}}{sen~61{}^\text{o}} = 6.99 cm\)
Ejemplo 2: Hallar β, γ y c en el siguiente triángulo si
• a = 28 cm
• b = 41 cm
• α = 39º
Respuesta
En este problema se dan dos lados y un ángulo que es opuesto a uno de ellos, y como se explicó previamente, podría haber dos soluciones. Para saberlo basta con verificar si a < b. Como a = 28 cm y b = 41 cm, en efecto existen dos posibilidades para el ángulo β. Mediante: \(\frac{\text{sen}~\alpha }{a}=\frac{\text{sen}~\beta }{b}\) Se halla la primera solución: \(\sin \beta =\frac{b\bullet sen~\alpha }{a}=~\frac{41~cm\bullet sen~39{}^\text{o}}{28~cm}=0.921505\) β1 = 67.147º
El otro ángulo cuyo seno vale 0.921505 es:
180 – 67.147º = 112.853º
El lector puede comprobarlo fácilmente con la calculadora, entonces:
β2 = 112.853º
Se deja como ejercicio para el lector encontrar el lado c y los ángulos β y γ de los dos triángulos posibles.
Respuestas:
γ1 = 73.853º, γ2 = 28.147º, c1 = 42.74 cm, c2 = 20.99 cm.

Trabajo publicado en: Abr., 2021.