Significado de vector Definición, componentes, y ejercicios

Licenciada en Física
Definición formal
Un vector es una entidad matemática abstracta que describe las propiedades de ciertas magnitudes físicas como la velocidad, la aceleración y la fuerza, entre muchas otras.
Sus magnitudes no se pueden especificar únicamente a través de un número, sino que poseen importantes características geométricas que es preciso tener en cuenta. La velocidad es una de estas magnitudes. Para entender totalmente la velocidad de un móvil, no es suficiente indicar que este se mueve a razón de 35 km/h, también hay que decir para dónde y en que sentido lo hace.
Otro ejemplo de una situación muy común: cuando una persona busca una calle, decirle que necesita caminar 5 km no es suficiente información para que llegue a su destino, porque la persona tiene que saber hacia dónde debe caminar para llegar donde desea, y eso significa especificar una dirección y un sentido.
Un vector es justamente lo que se necesita para dar toda la información precisa. Gráficamente, un vector se dibuja como una flecha, cuyo tamaño es proporcional a su magnitud, el ángulo que forma con una línea de referencia es su dirección y la punta de la flecha da el sentido.
Con un vector se le informa a las personas hacia dónde dirigirse para llegar a su destino, así como la velocidad que se necesita. También informan cómo aplicar las fuerzas para obtener un efecto deseado y cómo es el campo gravitatorio de un planeta o los campos electromagnéticos de las cargas. Los vectores tienen innumerables aplicaciones en la ciencia.
Componentes del vector: magnitud, dirección y sentido
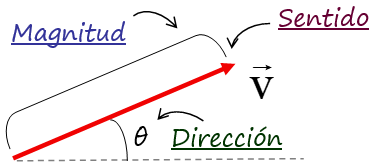
– La magnitud o módulo es proporcional al tamaño de la flecha que lo representa.
– La dirección del vector es la misma que la de la recta que lo contiene, así que escogiendo una línea de referencia, que puede ser la horizontal o la vertical, la dirección está dada por el ángulo θ que forma la recta con dicha línea referencial.
– Por último el sentido se indica a través de la punta de la flecha en el extremo del vector.
Notación para vectores
A los vectores se les denota con una letra con una flecha encima, así:\(\vec{v}\). Esta notación es apropiada para texto manuscrito, pero también son apropiadas las negritas en texto impreso, así que un vector puede denotarse como v, u, w u otra letra del alfabeto que se considere conveniente.
Cuando se trabaja con vectores es necesario denotarlos apropiadamente para distinguirlos de su magnitud o módulo, la cual utiliza letra normal o las barras de valor absoluto:
\(\left| {\vec{v}} \right|=v\)
Componentes cartesianas de un vector en el plano
Los vectores mostrados en las figuras anteriores son vectores libres, es decir, no están aplicados a un punto en particular. Pero cuando se conoce su punto de partida u origen y su extremo o punto de llegada, el vector queda totalmente especificado.
Si al origen del vector se lo hace coincidir con el origen de un sistema de coordenadas cartesianas, entonces es suficiente conocer su extremo para que el vector quede definido inequívocamente.
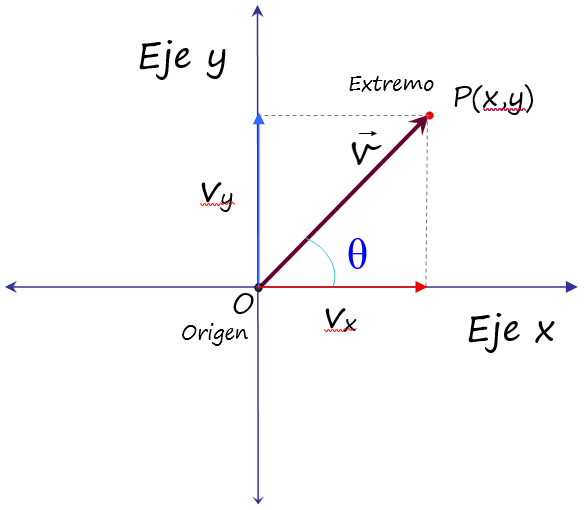
A las proyecciones del vector v con los ejes cartesianos se les llama componentes cartesianas del vector. Por ejemplo, el vector cuyo origen está en O(0,0) y el extremo está en P(5,3), tiene coordenadas cartesianas:
vx = 5
vy = 3
Al conocer estas proyecciones o componentes, el vector queda totalmente especificado. De acuerdo a esto, el vector v se puede expresar como:
\({\vec v}=\left\langle {{v}_{x}},{{v}_{y}} \right\rangle \)
Se usan corchetes para distinguir al vector de un punto, ya que para estos se emplean los paréntesis. El vector del ejemplo quedaría como:
\({\vec v}=\left\langle 5,3 \right\rangle \)
Forma polar de un vector en el plano
Si las componentes cartesianas de un vector se conocen, se puede especificar al vector en forma polar, que consiste en dar su módulo o magnitud y el ángulo que forma con el eje de referencia, usualmente el eje x positivo.
Sea θ el ángulo que forma el vector con el eje x, entonces por trigonometría elemental, las componentes cartesianas están relacionadas con el módulo y el ángulo θ a través de:
\({v_x}=\left| {\vec v} \right|\cdot \cos \theta \)
\({v_y}=\left| {\vec v} \right|\cdot sen\theta \)
El módulo se calcula a través del teorema de Pitágoras:
\(\left| {\vec v} \right|=v=\sqrt{\text{v}_{\text{x}}^{\text{2}}+\text{v}_{\text{y}}^{\text{2}}}\)
Y el ángulo θ que el vector forma con el eje +x es:
\(\theta =\text{arc tg}\frac{{{\text{v}}_{\text{y}}}}{{{\text{v}}_{\text{x}}}}\)
De modo que el vector queda especificado completamente:
\(\text{\vec{v}}=\text{(v}\text{,}\theta \text{)}\)
Ejercicios
1) Calcular las coordenadas cartesianas de los vectores y representarlos gráficamente:
a) v = (2, 30º)
b) u = (3, 135º)
Respuesta a
Mediante:
\({{\text{v}}_{\text{x}}}=\left| {\vec v} \right|\cdot \cos \theta \)
\({{\text{v}}_{\text{y}}}=\left| {\vec v} \right|\cdot sen\theta \)
Se sustituyen los valores dados:
\({{\text{v}}_{\text{x}}}=\text{2}\cdot \text{cos 30 }\!\!{}^\text{o}\!\!\text{ }=\text{2}\cdot \frac{\sqrt{\text{3}}}{\text{2}}=\sqrt{\text{3}}\)
\({{\text{v}}_{\text{y}}}=\text{2}\cdot \text{s}en\text{ 30 }\!\!{}^\text{o}\!\!\text{ }=\text{2}\cdot \frac{\text{1}}{\text{2}}=\text{1}\)
Respuesta b
\({{\text{u}}_{\text{x}}}=\text{3}\cdot \text{cos 135 }\!\!{}^\text{o}\!\!\text{ }=\text{2}\cdot \left( -\frac{\sqrt{\text{2}}}{\text{2}} \right)=-\sqrt{\text{2}}\)
\({{\text{u}}_{\text{y}}}=\text{2}\cdot \text{s}en\text{ 135 }\!\!{}^\text{o}\!\!\text{ }=\text{2}\cdot \frac{\sqrt{\text{2}}}{\text{2}}=\sqrt{\text{2}}\)
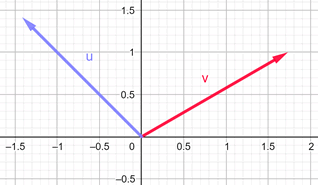
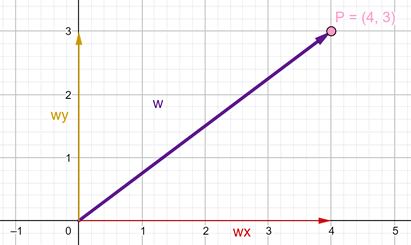
2) En base a las coordenadas cartesianas de un vector w determinadas como
wx = 4
wy = 3
Graficar este vector y determinar su módulo y el ángulo que forma con el eje x positivo.
Respuesta
Para calcular la magnitud o módulo del vector se emplea:
\(\left| {\vec w} \right|=w=\sqrt{\text{w}_{\text{x}}^{\text{2}}+\text{w}_{\text{y}}^{\text{2}}}=\sqrt{{{\text{4}}^{2}}+{{\text{3}}^{2}}}=\sqrt{16+\text{9}}=\sqrt{\text{25}}=\text{5}\)
Y el ángulo que forma w con la horizontal es:
\(\theta =\text{arc tg}\frac{{{\text{w}}_{\text{y}}}}{{{\text{w}}_{\text{x}}}}=\text{arc tg }\frac{\text{3}}{\text{4}}=\text{36}\text{.9 }\!\!{}^\text{o}\!\!\text{ }\)
Finalmente, la gráfica del vector es:

Trabajo publicado en: Ene., 2021.