Significado de energía cinética Definición, deducción, trabajo, inercia y calculadora
Definición formal
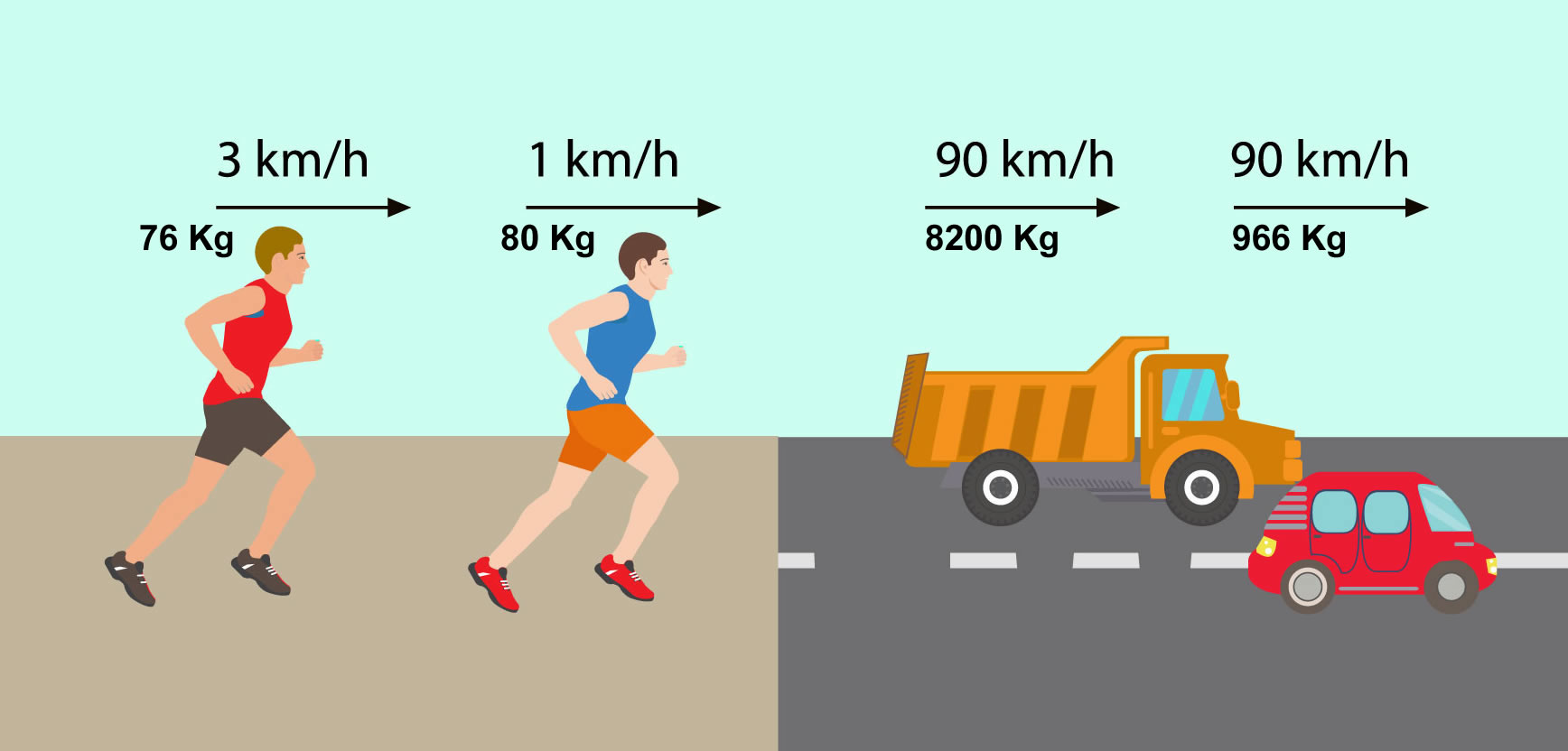
La energía cinética es atribuida a la energia que está vinculada al movimiento de un cuerpo, determinado por su masa (representado por m) y velocidad (por v), cuyo cálculo es posible a partir de la multiplicación de la mitad de su masa por el cuadrado de la rapidez con la que se mueve.
La energía cinética se expresa matemáticamente en
\(E_{c} = \frac{1}{2} mv^2\)
De este modo se observa que, si el movimiento duplica, triplica y cuadruplica, la energía cinética que le compete crece cuatro, nueve y dieciséis veces respectivamente, percibiendo un claro incremento exponencial.
Por ejemplo, una persona que está corriendo no tiene las mismas propiedades ni posibilidades que un vehículo automotriz, de hecho ni siquiera es posible igualar a un individuo con otro, razón por la cual solamente existe un único Usain Bolt, quien incluso ha sido objeto de estudio en numerosas oportunidades por la física y el campo de la energía cinética en particular, por caso, en Berlín 2009, en la competencia de 100m, calculando en base a su peso de 86 kg y una velocidad máxima de 12 m/s registrada a los 65m, se obtuvo como resultado 6192 joules, tal como puede comprobarse en la calculadora o ejercitarse.
No obstante, la energía cinética puede perder fuerza por la intervención de fuerzas disipadoras o a efectos de la energía potencial; no es lo mismo, por ejemplo, avanzar de un punto a otro sobre una zona llana a hacerlo sobre una pendiente.
Según la oficina internacional de pesos y medidas, cuya sede se ubica en Francia, encargada de establecer las unidades del Sistema Internacional (SI), toda energía se expresa en Joules (o Julios) como unidad de medida, donde 1J=1N•m. Sin embargo, existen otra formas para expresar energía como: la caloría (cal), electronvoltio (eV) kilovatio-hora (kWh), tonelada equivalente de carbón (tec) y la tonelada equivalente de petróleo (tep), entre otras.
Diferencias entre la energía cinética y la energía potencial

La energía cinética es una forma de energía mecánica, por lo que parte de su definición esta ligada a la capacidad que tiene un sistema de realizar trabajo. Sin embargo, es importante puntualizar las diferencias entre la energía cinética y otra forma básica de energía mecánica: la energía potencial.
La energía potencial se debe a una fuerza conservativa, lo que implica que no depende del movimiento o recorrido de un cuerpo, sino de la posición que éste ocupe en un momento dado. Algunos ejemplos de fuerza conservativa son: gravedad, electricidad, magnetismo y elasticidad (ley de Hook).
Sin embargo, la energía cinética no depende directamente de una fuerza sino de su movimiento como tal y una propiedad intrínseca de la materia: la inercia. En este caso, su deducción viene de analizar el trabajo realizado sobre un cuerpo durante su movimiento que, mediante algunos artilugios matemáticos, no dependerá de su posición sino de la rapidez del cuerpo en un instante determinado
Deducción de la ecuación que calcula energía cinética: Trabajo y Segunda Ley de Newton

Primero debemos recordar que las energías mecánicas, como lo es la energía cinética, tienen por principio la capacidad de realizar trabajo por lo que su definición viene dada por la siguiente ecuación:
W=F•∆r•cos(𝛂)
Donde F es la fuerza aplicada sobre un cuerpo, ∆r se refiere al desplazamiento entre dos puntos cuáles quieras r1 y r2 y 𝛂 es el ángulo entre los vectores F y ∆r.
Para nuestro análisis, la fuerza que provoca el cambio de velocidad será paralela al desplazamiento del cuerpo, por lo que los vectores F y ∆r serán paralelos y apuntando en la misma dirección. Por esto, el ángulo 𝛂 tendrá un valor de 0°, con cos(0°)=1.
En el mismo orden de ideas, no pondremos atención en una fuerza específica que provoque el cambio de la velocidad, sino que trabajaremos sobre la fuerza neta aplicada que genera el cambio de movimiento que genera el cambio de movimiento.
W=F•∆r
Según la segunda ley de Newton en su forma fundamental, la fuerza neta que actúa sobre un cuerpo es igual al cambio en la cantidad de movimiento de éste. Al utilizar la segunda ley de Newton junto con el concepto de trabajo obtenemos el siguiente hilo de ecuaciones:
F=∆p
W=F•∆r
W=∆p•∆r
Donde ∆p se refiere al cambio en la cantidad de movimiento, o simplemente cambio de momentum. Para situaciones de masa constante donde ∆p=m•∆v, la última expresión de trabajo puede reorganizarse de la siguiente forma:
W=(m•∆v)/∆t•∆r
W=m•(∆v/∆t)•∆r
W=m•a•∆r
Esta expresión de trabajo nos permite determinar la energía, al combinar ésta con una de las ecuaciones básicas del MRUV:
Vf=Vi+2•a•∆r
De donde despejaremos a•∆r, ya que está en la ecuación de trabajo que venimos organizando
a•∆r=Vf/2 – Vi/2.
Al sustituir ésta en la expresión que se dedujo de trabajo, nos queda la siguiente ecuación:
W=½mVf²-½mVi²
(Agregar una imagen de un mismo cuerpo en dos instantes diferentes con velocidades diferentes)
Como en este caso el trabajo no está directamente relacionado a una fuerza, se toman las expresiones del miembro derecho como un nuevo tipo de energía mecánica: energía cinética.
Ec=½m•v²
Esta expresión nos permite determinar la energía asociada a un cuerpo de masa m que se desplaza con cierta velocidad v.
Energía cinética e inercia

La inercia es uno de los conceptos básicos de la mecánica, ideado por Isaac Newton junto a sus tres leyes del movimiento. Sin embargo, esta propiedad no es medible directamente, es deducible indirectamente al medir la masa y está asociada al movimiento como tal que tiene el cuerpo (su velocidad). Por esto, aunque dos cuerpos tengan la misma masa, no podemos asegurar que tengan la misma inercia. Esto se debe al aporte de la velocidad sobre la inercia del cuerpo, ¿Cuánto es este aporte de la velocidad sobre la inercia de un cuerpo?
Para responder a esta pregunta nos remitimos a la energía mecánica del cuerpo, haciendo el supuesto de que es un cuerpo que se desplaza libremente en MRU sin la acción de ninguna otra fuerza. Así, solo puede tener energía cinética. Ésta es la energía que debemos aplicar con alguna otra fuerza para detenerlo, es decir, la energía cinética es una forma indirecta de inercia.
Ejercicios ilustrativos
1. Un vehículo de masa 450kg se desplaza con una rapidez de 15m/s por una carretera totalmente horizontal. Si el conductor decide detenerse, ¿Cuánta energía debe perder el vehículo?
(Agregar imagen del vehículo frenando)
En este caso la única energía mecánica asociada al vehículo es la energía cinética, y es la que al final del planteamiento se hará cero (Vf=0)
Por esto solo debemos aplicar la ecuación de la energía cinética para calcular la energía
\(E_{c} = \frac{1}{2} mv^2\)
\(E_{c} = \frac{1}{2} \cdot \left ( 450kg \right ) \cdot \left ( 15m/s \right )^2\)
\(E_{c} = \frac{1}{2} \cdot 450 \cdot 225 (kg \cdot m/s^2)\)
\(E_{c} = 25312,5 J\)
El vehículo debe perder 25312,5 Joules de energía para detenerse completamente.
2. ¿Cuál es el punto máximo de energía cinética alcanzado durante el trayecto de los 100m por Usain Bolt en Rusia 2009, sabiendo que su masa corporal está dada por 86 Kg, y su velocidad en 12 m/s , registrándose como tal sobre los 65m de la pista?
\(E_{c} = \frac{1}{2} \cdot \left ( 86kg \right ) \cdot \left ( 12m/s \right )^2\)
\(E_{c} = \frac{1}{2} \cdot 86 \cdot 114 (kg \cdot m/s^2)\)
\(E_{c} = 6192 J\)
Calculadora de energía cinética
Trabajo publicado en: Oct., 2020.
Ilustraciones: Fridas, Woters, Aldona, Designua