Significado de la ley de Gauss Definición, campo eléctrico (flujo y superficie)

Licenciada en Física
Definición formal
La ley de Gauss expresa en forma matemática la relación existente entre el campo eléctrico E en cada punto de una superficie, con la carga eléctrica encerrada en su interior qdentro, a través de la magnitud escalar determinada como flujo de campo eléctrico Φneto
1) \({{\Phi }_{{neto}}}=\frac{{{{q}_{{dentro}}}}}{{{{\varepsilon }_{o}}}}\)
Esta ecuación se interpreta de la siguiente forma: el flujo neto que pasa a través de una superficie de propiedad cerrada resulta proporcional a la carga que ésta encierra, siendo 1/εo la constante de proporcionalidad, con
εo = 8.85 ×10-12 C2 / N∙m2
Esta es la permitividad eléctrica del vacío. Para algunos es más familiar expresar la constante de proporcionalidad en términos de la constante electrostática k que aparece en la ley de Coulomb
2)\({{\Phi }_{{neto}}}=4\pi k{{q}_{{dentro}}}\)
Donde \(k\approx 9\times {{10}^{9}}N\cdot {{m}^{2}}/{{C}^{2}}\) y está relacionada con εo a través de
\(k=\frac{1}{{4\pi {{\varepsilon }_{o}}}}\)
Las unidades del flujo de campo eléctrico en el Sistema Internacional son N∙m2 /C. Nótese que para calcular Φneto solo se necesita conocer la carga contenida dentro de la superficie, y a la inversa, si se conoce la carga dentro de una superficie cerrada, el cálculo del flujo eléctrico neto es inmediato.
Por ejemplo ¿Cuál es la carga neta qdentro encerrada por una superficie, sabiendo que el flujo a través de ella es 9.57 ×106 N∙m2 /C?
El valor solicitado se despeja fácilmente de la ley de Gauss
qdentro = Φ∙εo = (9.57 ×106 N∙m2 /C) × 8.85 ×10-12 C2 / N∙m2 = 8.47×10-5 C.
Es interesante destacar que el resultado es completamente independiente de la superficie, ya que el flujo neto a través de ella depende solo de la carga que lo produce.
El flujo de campo eléctrico Φ
Dado a través de una superficie, abierta o cerrada, es una cantidad escalar que se calcula empleando alguna de estas expresiones, de acuerdo al caso
3) \(\Phi =\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E}\bullet \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}A=EA\cos \theta\) , para un campo eléctrico uniforme y una superficie constante A.
4) \(\Phi =\int_{S}{\vec{E}\bullet \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}dA}=\int_{S}{E\cdot \cos \theta }\cdot dA\) , si el campo no es uniforme y/o el área no es constante, esta última expresión es la más general de todas, puesto que la ecuación 3 es un caso particular.
En ambas ecuaciones \(\hat{n}\) es un vector normal unitario (de módulo igual a 1) a la superficie, que se usa para determinar la orientación de esta en el espacio, θ es el ángulo entre \(\vec{E}\) y \(\hat{n}\) y finalmente el subíndice S representa la superficie sobre la que se va a evaluar la integral.
El flujo de campo eléctrico es, pues, una medida de la cantidad de líneas de campo eléctrico que pasan a través de la superficie S, ya sea abierta o cerrada.
Flujo de campo eléctrico a través de superficies cerradas
Si la superficie es cerrada y Φ es nulo, ocurre que la carga neta dentro de la superficie es 0, lo cual significa que alguna de estas dos alternativas es cierta:
i) La superficie no encierra carga alguna, por lo tanto ningún agente produce líneas de campo eléctrico.
ii) En el interior de la superficie hay igual número de cargas positivas y negativas, de manera que la carga neta es 0.
En la siguiente imagen, el flujo de campo eléctrico que atraviesa la superficie cerrada e irregular es 0, pues en el interior hay dos cargas de igual magnitud y signo contrario, separadas una pequeña distancia. A esta configuración se la llama dipolo eléctrico y es un buen modelo para representar algunas moléculas, como la del agua, por ejemplo.
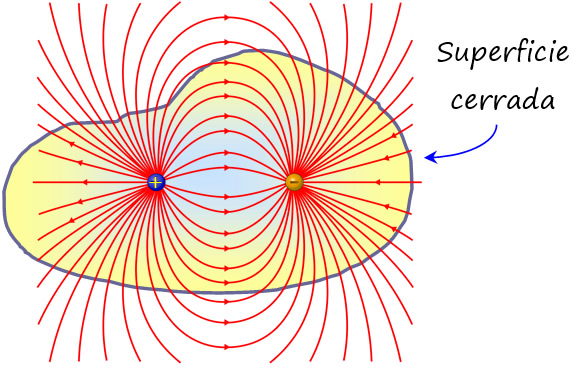
Si las líneas de flujo son salientes a la superficie (cerrada), el flujo es positivo y si las líneas son entrantes, el flujo es negativo. Así pues, el signo del flujo es el mismo que el de la carga neta.
Calcular el campo eléctrico a través de la ley de Gauss
La integral de flujo en la ecuación 4 se puede igualar a la ecuación 1 o a la ecuación 2, ya que ambas representan el flujo de campo eléctrico.
Al hacerlo, se presenta la ocasión de calcular el campo eléctrico partiendo de la integral para el flujo, solamente si la superficie S (cerrada) que encierra la carga tiene la simetría adecuada como para que el cálculo analítico resulte sencillo.
A la superficie S se la llama superficie gaussiana y la ley de Gauss constituye una alternativa a la ley de Coulomb para calcular campos eléctricos con distribuciones de carga de alta simetría.
Lo que se plantea para ello es
5) \(\Phi =\int_{S}{\vec{E}\bullet \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}dA}=\frac{{{q}_{dentro}}}{{{\varepsilon }_{o}}}\)
6) \(\int_{S}{\vec{E}\bullet \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}dA}=\frac{{{q}_{dentro}}}{{{\varepsilon }_{o}}}\)
También en ocasiones se utiliza esta notación con un pequeño círculo en la integral representando la superficie cerrada, que es equivalente a colocar el subíndice S
7) \(\oint{\vec{E}\bullet \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}dA}=\frac{{{q}_{dentro}}}{{{\varepsilon }_{o}}}\)
Para que la ley de Gauss sea útil en el cálculo del campo eléctrico, es necesario que este sea constante en toda la superficie gaussiana S. Además hay que conocer la carga neta encerrada por S.
El procedimiento general para aplicar la ley de Gauss es el siguiente:
1.- Identificar la geometría de la distribución (generalmente esférica, plana o cilíndrica).
2.- Seleccionar la superficie gaussiana apropiada que contenga al punto donde se desea calcular el campo. Si la simetría de la distribución de carga es esférica se elige una superficie gaussiana esférica, si se trata de una línea delgada o un cilindro de carga, la gaussiana será cilíndrica y si la distribución de carga es plana, una superficie cilíndrica también puede ser apropiada.
3.- Dividir la superficie en partes, de tal manera que se cumpla alguna de estas dos condiciones:
i) \(\vec{E}\) y \(\hat{n}\) sean paralelos (θ=0), en cuyo caso el producto escalar y sean paralelos (θ=0), en cuyo caso el producto escalar \(\vec{E}\bullet \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}dA=EdA\cos 0=EdA\)
ii) \(\vec{E}\) y \(\hat{n}\) sean perpendiculares (θ=90º), para que el producto escalar se anule: \(\vec{E}\bullet \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}dA=EdA\cos 90{}^\text{o}=0\)
Si se cumple la condición i), la integral \(\oint{{E\cdot dA}}\) es simplemente \(E\cdot A\) y si se cumple ii), entonces la integral se anula en esa parte.
4.- Evaluar la carga neta en el interior de S (qdentro) y despejar la magnitud del campo como
8) \(E=\frac{{{{q}_{{dentro}}}}}{{{{\varepsilon }_{o}}A}}\)
5.- Asignar la dirección y el sentido correctos al campo para expresarlo como vector.
Ejercitación práctica
Se tiene una carga eléctrica positiva Q, distribuida uniformemente sobre una esfera maciza no conductora de radio a. Calcular el campo eléctrico de esta distribución en un punto ubicado a una distancia \(r < a\) del centro de la esfera. Respuesta
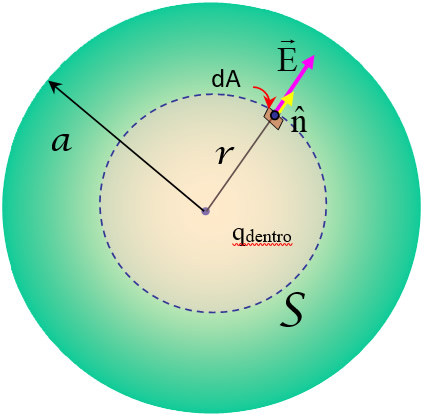
La simetría es esférica, por lo tanto se elige una superficie gaussiana S esférica (representada en la figura con línea punteada), que pasa por un punto localizado a una distancia radial r del centro de la esfera. El valor de r es el radio de la gaussiana S.
Ahora se toma un diferencial de área dA representativo, como el que se señala en la figura (flechita roja curva). Sobre esa área infinitesimal, el vector campo eléctrico \(\vec{E}\)(fucsia) es paralelo al vector normal unitario \(\hat{n}\)(amarillo) y saliente a S, por ser Q positiva.
Esto se cumple para cualquier otro diferencial de área que se tome sobre la superficie gaussiana S, por lo que es seguro afirmar que:
\(\vec{E}\bullet \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}dA=E\cdot dA\cdot \cos 0=EdA\)
Y al integrar queda:
\(\int_{S}{EdA=E\int_{S}{dA=}E\cdot A}\)
Con A igual al área de la superficie gaussiana S y valor 4πr2.
Ahora hay que evaluar la carga en el interior de S, cuyo valor obviamente es menor que Q.
Como la densidad volumétrica de carga ρ es constante, ya que el enunciado afirma que “…la carga está distribuida uniformemente”, entonces la carga contenida en la esfera de radio r (volumen encerrado por S) es:
\(\rho =\frac{c\arg a}{volumen}=\frac{{{q}_{dentro}}}{\frac{4}{3}\pi {{r}^{3}}}\)
Se despeja qdentro:
\({{q}_{dentro}}=\frac{4}{3}\pi \rho {{r}^{3}}\)
Donde la densidad de carga es:
\(\rho =\frac{Q}{\frac{4}{3}\pi {{a}^{3}}}\)
El siguiente paso es sustituir todo en la ecuación 8, simplificando al máximo el resultado:
\(E=\frac{{{q}_{dentro}}}{{{\varepsilon }_{o}}A}=\frac{\frac{4}{3}\pi \rho {{r}^{3}}}{{{\varepsilon }_{o}}4\pi {{r}^{2}}}=\left( \frac{\rho }{3{{\varepsilon }_{o}}} \right)r=\left( \frac{Q}{4\pi {{\varepsilon }_{o}}{{a}^{3}}} \right)r\)
Y para finalizar, dado que el campo es radial, se le asigna la dirección \(\hat{r}\), por lo tanto el vector campo eléctrico queda:
\(\vec{E}=\left( {\frac{{Qr}}{{4\pi {{\varepsilon }_{o}}{{a}^{3}}}}} \right)\hat{r}\)

Trabajo publicado en: Feb., 2021.