Significado de regularización (en matemáticas) Definición, explicación, fórmula, y tipos

Doctor en Ingeniería
Definición formal
La regularización es la acción de forzar ciertas características sobre la solución a la hora de resolver un Problema Inverso.
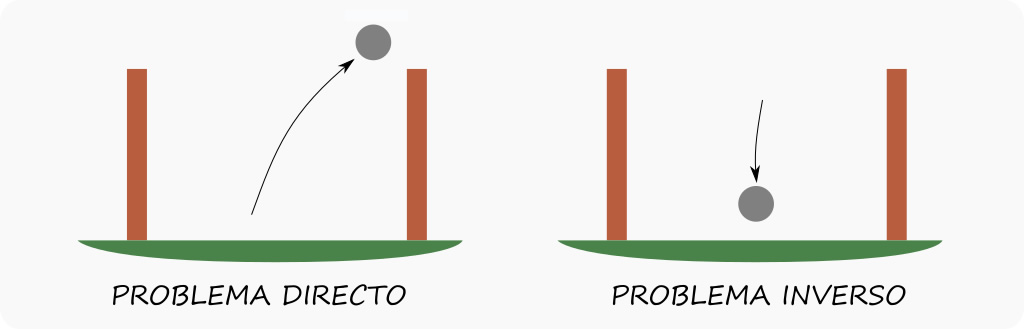
Para ilustrar la definición, supongamos que estamos en el patio, pateamos la pelota y se va sobre la medianera. Tratar de decidir a qué vecino ir a golpearle la puerta habiendo visto en qué dirección fue la pelota es lo que se conoce como un problema directo: es decir, tratar de estimar la consecuencia a partir de la causa. Si en cambio estamos en el patio y encontramos una pelota, tratar de averiguar a qué vecino se le perdió es un problema inverso (buscar la causa dada la consecuencia) y generalmente es mucho más difícil.
Al problema directo puedo resolverlo (casi siempre) a partir de haber observado la dirección y velocidad con que salió la pelota. Para resolver el problema inverso, en cambio, puedo suponer que la pelota vino de una de las casas inmediatamente al lado, y probablemente de una casa en que viven niños. Es decir, que para encarar el problema inverso estoy incorporando información externa, que me ayude a resolverlo. Esto es lo que se busca con la Regularización.
Fórmula matemática que expresa la Regularización
Consideremos (por simplicidad) el sistema lineal
\(Ax=y\) ,
donde \(A \in \mathbb{R}^{M\times N}\) e \(y\in\mathbb{R}^M\) son conocidos, y queremos hallar x. Esto constituye un problema inverso, dado que conocemos «la consecuencia» y y queremos recuperar el vector x que la generó.
Si A es una matriz pequeña e invertible, este problema puede resolverse de manera trivial como \(x = A^{-1}y\). No obstante, si M < N, o si M = N pero A tiene autovalores iguales o muy cercanos a cero, el sistema no puede resolverse invirtiendo la matriz A.
Si A no es invertible, podemos intentar resolver nuestro problema utilizando la inversa generalizada de Moore-Penrose, que no es otra cosa que hallar el valor de x que minimiza
\(\|Ax-y\|^2_2\) .
Esto nos da una solución, llamada de mínimos cuadrados para el sistema, pero aún así podría no ser suficiente.

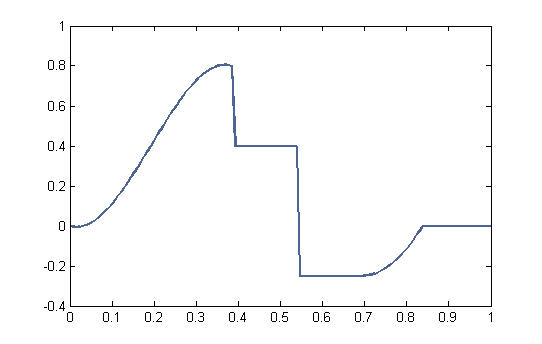
Consideremos un ejemplo real, ilustrado en la Figura 2. Aquí se ve la observación y generada con una matriz \(A\in\mathbb{R}^{N\times N}\) (de blurring o suavizado) y un poco de ruido, a partir de una señal x que supondremos desconocida y que queremos recuperar.
Si en este caso intentamos utilizar la solución de mínimos cuadrados
\(\hat{x} = \text{argmin}_x \|Ax-y\|^2_2\) ,
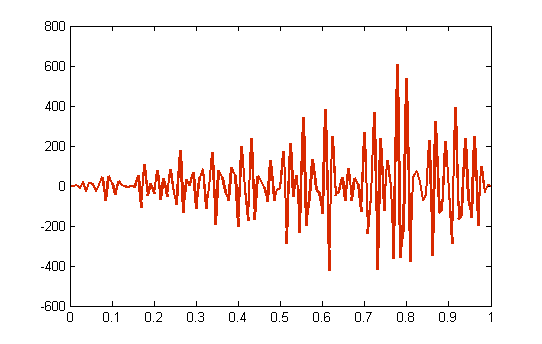
obtendremos una solución como se ve en la Figura 4, que claramente no tiene nada que ver con la señal x que queremos recuperar.
Es aquí donde entra en juego la regularización. Al igual que en el primer ejemplo habíamos supuesto que la pelota no podía haber venido de muy lejos, aquí podemos suponer que la señal original no tiene oscilaciones violentas, agregando un término de regularización a la función que queremos minimizar. De esta forma, una solución regularizada del sistema, se escribe como
\(\hat{x} = \text{argmin}_x \left(\|Ax-y\|^2_2 +P(x)\right)\) ,
donde P(x) es una función que impone suavidad a x.
Tipos de Regularizante
Dependiendo del problema que tengamos delante, el término de regularización P(x) puede tomar muchas formas. El más clásico es el regularizante de tipo Tikhonov-Phillips \(P(x) = \lambda \|x\|^2\), donde \(\lambda >0\) determina el peso (o la importancia) que le daremos a la regularización. Este tipo de regularizantes produce soluciones como las que vemos en la Figura 5.
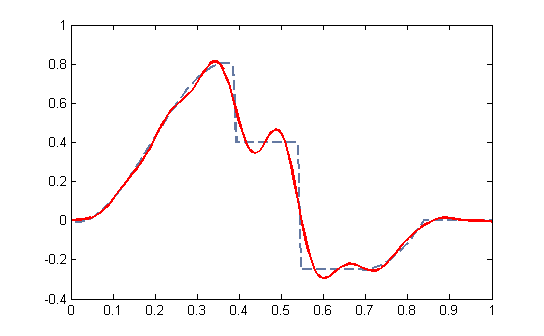
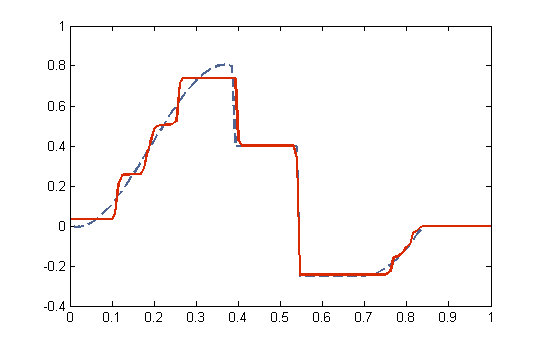
Esta regularización produce una solución «suave» que no permite reconstruir bien los saltos en la señal, por lo que se han desarrollado otras formas de regularización tipo Variación Total y combinaciones y modificaciones que permiten obtener resultados de mejor calidad (Figura 7).

Existen muchos otros tipos de regularización, que varían según el campo de aplicación, pero el principio siempre es el mismo. Ya sea regularizando los pesos en Redes Neuronales Artificiales, resolviendo problemas de Regresión o Aproximación, lo que hacemos es incorporar información que nos ayude a deducir de dónde vino la pelota.

Trabajo publicado en: Feb., 2021.