Significado de sucesiones cuadráticas Definición, primeras y segundas diferencias

Licenciada en Física
Definición formal
Las sucesiones cuadráticas son un conjunto de elementos ordenados, en el que cada valor se calcula con base a una regla determinada.
La forma matemática que explica las sucesiones cuadráticas está dada como
an2 + bn + c
Con a, b y c como números reales. Se afirma que la sucesión es cuadrática porque la regla para encontrar sus elementos es expresión cuadrática. Los elementos de la sucesión pueden ser números, funciones u otros.
¿Y quién es n? Pues es un número natural que señala la posición que ocupa el elemento en la sucesión. Para hallar cada uno, se sustituyen los valores de n en la fórmula de la sucesión, comenzando por n =1, luego n= 2 y así sucesivamente.
A cada uno de los términos de la sucesión se los suele identificar mediante una letra del alfabeto, como la “a” por ejemplo, acompañada del subíndice “n”, que indica su posición. Así
a1, a2, a3, a4…
Entonces, a1 es el primer término, a2 el segundo, a3 el tercero, hasta llegar a an que es el término “enésimo” y viene dado precisamente por la regla
an = an2 + bn + c
De esta manera, construir una sucesión cuadrática conociendo la forma de su término enésimo es muy sencillo. Por ejemplo, supóngase que la regla de la sucesión viene dada por
2n2 – n – 1
Los primeros cinco términos son
Para n = 1:
a1=2 ∙ 12 – 1 – 1 = 0
Para n = 2:
a2=2 ∙ 22 – 2 – 1 = 5
Para n = 3:
a3=2 ∙ 32 – 3 – 1 = 14
Para n = 4:
a4=2 ∙ 42 – 4 – 1 = 27
Para n = 5:
a5 = 2 ∙ 52 – 5 – 1 = 44
La sucesión del ejemplo es, por tanto
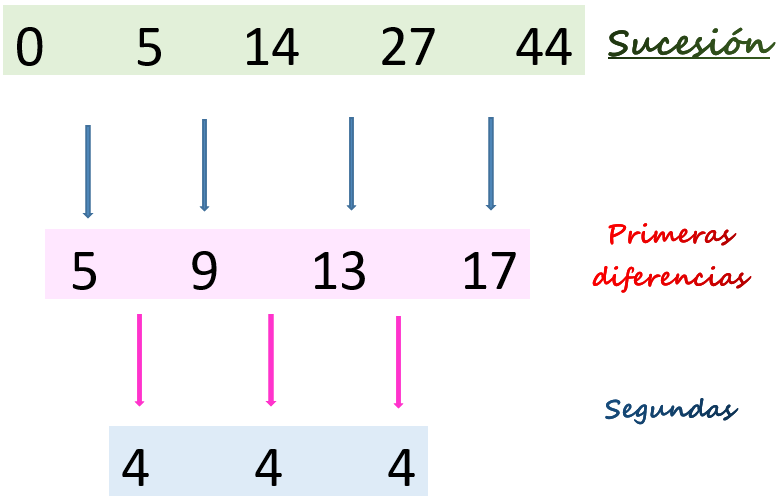
0, 5, 14, 27, 44…
Los puntos suspensivos indican que hay infinitos términos.
Primeras y segundas diferencias
A los matemáticos les gusta mucho observar patrones en series de números y en las sucesiones cuadráticas hay uno muy interesante. Se encuentra a través de las diferencias entre los términos, llamadas primeras diferencias, y luego calculando las diferencias de las diferencias, que son las segundas diferencias.
Es muy fácil encontrarlas. Para las primeras diferencias hay que efectuar
a2 – a1; a3 – a2, a4 – a3, a5 – a4 …
Tomando los resultados del ejemplo anterior, las primeras diferencias son
a2 – a1 = 5 – 0 = 5
a3 – a2 = 14 – 5 = 9
a4 – a3 = 27 – 14 = 13
a5 – a4 = 44 – 27 = 17
De esta manera se ha encontrado una nueva sucesión de números, los cuales son
5, 9, 13, 17…
Y hasta ahora parece que no hay nada especial acerca de ellos, pero ahora se calculan las diferencias de estas primeras diferencias, que son las segundas diferencias
9 – 5 = 4
13 – 9 = 4
17 – 13 = 4
Ahora sí se evidencia un patrón, ya que todas las segundas diferencias tienen el mismo valor, en este ejemplo es 4.
Pues bien, ocurre que las segundas diferencias de una sucesión cuadrática siempre valen lo mismo, es decir, son constantes y diferentes de 0.
Este hecho ofrece la oportunidad de determinar cuando una sucesión es cuadrática: si se tiene una sucesión, simplemente se calculan las primeras diferencias y luego las segundas. Si estas valen siempre lo mismo, es cuadrática, y si tienen distinto valor, entonces no lo es.
Término enésimo de la sucesión cuadrática
Anteriormente se vio que es muy fácil encontrar los términos de la sucesión conociendo el término enésimo, dado por
an = an2 + bn + c
Únicamente hay que sustituir n por 1,2,3,4… y efectuar la operación respectiva.
Ahora se quiere proceder a la inversa, es decir, hallar el término enésimo si se conocen algunos términos de la sucesión. Para ello el preciso calcular los valores de a, b y c en an.
Por ejemplo, se tiene la sucesión dada por
−4, −1, 4, 11, 20, …
El primer paso es comprobar que sea cuadrática, hallando las primeras y segundas diferencias
a2 – a1 = – 1 – (–4) = 3
a3 – a2 = 4 – (–1) = 5
a4 – a3 = 11 – 4 = 7
a5 – a4 = 20 – 11 = 9
Luego
5 – 3 = 2
7 – 5 = 2
9 – 7 = 2
Como las segundas diferencias valen lo mismo, la sucesión es cuadrática.
El segundo paso es encontrar expresiones para al menos tres de sus términos, en las que, por supuesto, aparecen las incógnitas a, b y c
a1 = a ∙ 12 +b ∙ 1 + c = -4
1) a + b + c = – 4
a2 = a ∙ 22 + b ∙ 2 + c = -1
2) 4a + 2b + c = – 1
a3 = a ∙ 32 + b ∙ 3 + c = 4
3) 9a + 3b + c = 4
Con las ecuaciones 1), 2) y 3) se forma un sistema de tres ecuaciones con tres incógnitas, que se resuelve por el método de preferencia, por ejemplo, la regla de Cramer o mediante una calculadora científica.
La solución del sistema es
a = 1; b = 0; c = –5
Lo que conduce al término enésimo dado por
an = n2 – 5
El lector puede comprobar que sustituyendo n = 1,2,3,4… en el término enésimo, se obtienen los valores de la sucesión dados en el ejemplo.

Trabajo publicado en: May., 2021.