¿Cómo se define el Teorema de Thales?

A partir del Teorema de Thales, dadas varias rectas paralelas, se dice que la línea \(T\) es transversal a las líneas paralelas si intersecta a cada una de las líneas paralelas.

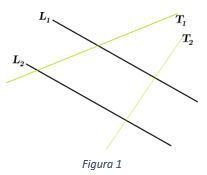
En la figura 1, las líneas \({T_1}\) y \({T_2}\) son transversales a las líneas paralelas \({L_1}\) y \({L_2}.\)

Teorema de Thales (versión débil)
Si varias paralelas determinan segmentos congruentes (que miden lo mismo) en una de sus dos rectas transversales, determinarán también segmentos congruentes en la otra transversales.

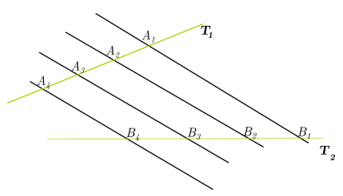
En la figura 2, las rectas negras son paralelas y se tiene que:
\({A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4}.\)
Podemos asegurar lo siguiente:
\({B_1}{B_2} = {B_2}{B_3} = {B_3}{B_4}.\)

Se cuenta que el sabio Thales de Mileto midió la altura de la pirámide de Keops, para ello usó sombras y la aplicación de las propiedades de semejanza de triángulos. El Teorema de Thales es fundamental para el desarrollo del concepto de semejanza de triángulos.

Razones y propiedades de las proporciones

Una razón es el cociente de dos números, con el divisor distinto de cero; es decir:

\(\frac{a}{b}\;{\rm{con\;}}b \ne 0\)

Una proporción es la igualdad de dos razones, es decir:

\(\frac{a}{b} = \frac{c}{d} = k,\)

\(k\) es llamada, también, constante de proporcionalidad.

Propiedades de las proporciones

Si \(\frac{a}{b} = \frac{c}{d} = k\) entonces para \(m \ne 0:\;\)

\(\frac{{ma}}{{mb}} = \frac{a}{b} = \frac{c}{d} = k\)

\(\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}} = \frac{{a – c}}{{b – d}} = k\)

\(\frac{a}{b} = \frac{c}{d} = \frac{f}{g} = \frac{{a + c + f}}{{b + d + g}} = k\)

\(\frac{{a \pm b}}{b} = \frac{{c \pm d}}{d}\)

Ejemplos

\(\frac{9}{{24}} = \frac{{15}}{{40}} = \frac{{9 + 15}}{{24 + 40}} = \frac{{24}}{{64}}\)

\(\frac{9}{{24}} = \frac{{15}}{{40}} = \frac{{15 – 9}}{{40 – 24}} = \frac{6}{{16}}\)

\(\frac{{9 + 24}}{{24}} = \frac{{15 + 40}}{{40}}\)\(\frac{{33}}{{24}} = \frac{{55}}{{40}}\)

El par de segmentos \(\overline {AB} \) y \(\overline {CD} \) se dice que son proporcionales a los segmentos \(\overline {EF} \) y \(\overline {GH} \) si se cumple la proporción:

\(\frac{{AB}}{{CD}} = \frac{{EF}}{{GH}}\)

Donde \(AB\;\)denota la longitud del segmento \(\overline {AB} .\)

Teorema de Thales

Retomando la definición, varias paralelas determinan segmentos correspondientes proporcionales en sus rectas transversales.

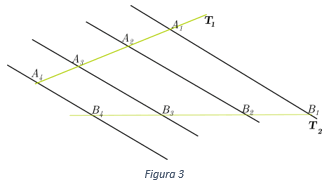
En la figura 3, las líneas rectas son paralelas y podemos asegurar:

\(\frac{{{A_1}{A_2}}}{{{A_2}{A_3}}} = \frac{{{B_1}{B_2}}}{{{B_2}{B_3}}}\)\(\frac{{{A_2}{A_3}}}{{{A_3}{A_4}}} = \frac{{{B_2}{B_3}}}{{{B_3}{B_4}}}\)\(\frac{{{A_2}{A_4}}}{{{A_2}{A_3}}} = \frac{{{B_2}{B_4}}}{{{B_2}{B_3}}}\)\(\frac{{{A_1}{A_2}}}{{{A_3}{A_4}}} = \frac{{{B_1}{B_2}}}{{{B_3}{B_4}}}\)\(\frac{{{A_1}{A_3}}}{{{A_1}{A_2}}} = \frac{{{B_1}{B_3}}}{{{B_1}{B_2}}}\)

Notemos que las dos primeras proporciones anteriores son equivalentes a las siguientes proporciones:

\(\frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}}\)\(\frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac{{{A_3}{A_4}}}{{{B_3}{B_4}}}\)De lo anterior obtenemos:

\(\frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac{{{A_3}{A_4}}}{{{B_3}{B_4}}} = \frac{{{A_1}{A_2} + {A_2}{A_3} + {A_3}{A_4}}}{{{B_1}{B_2} + {B_2}{B_3} + {B_3}{B_4}}} = \frac{{{A_1}{A_4}}}{{{B_1}{B_4}}}\)

En muchas ocasiones es mejor trabajar con las proporciones anteriores y en este caso:

\(\frac{{{A_i}{A_j}}}{{{B_i}{B_j}}} = k\)

Recíproco del Teorema de Thales

Si varias rectas determinan segmentos correspondientes proporcionales en sus rectas transversales entonces las rectas son paralelas

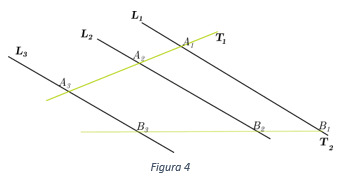
Si en la figura 4 se cumple

\(\frac{{{A_1}{A_2}}}{{{A_2}{A_3}}} = \frac{{{B_1}{B_2}}}{{{B_2}{B_3}}}\)

Entonces podemos afirmar que: \({L_1}\parallel {L_2}\parallel {L_3}.\)

La notación \({L_1}\parallel {L_2}\), se lee \({L_1}\) es paralela a \({L_2}\).

De la proporción anterior se obtiene:

\(\frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac{{{A_1}{A_2} + {A_2}{A_3}}}{{{B_1}{B_2} + {B_2}{B_3}}} = \frac{{{A_1}{A_3}}}{{{B_1}{B_3}}}\)

División de un segmento en varias partes de igual longitud

Mediante un ejemplo concreto ilustraremos como dividir un segmento en partes de igual longitud.

Dividir el segmento \(\overline {AB} \) en 7 segmentos de igual longitud

Situación inicial

Se traza una recta auxiliar que pase por uno de los extremos del segmento

Con apoyo de un compás se trazan 7 segmentos de igual longitud sobre la recta auxiliar

Se traza la recta que une los extremos del último segmento trazado y el otro extremo del segmento a dividir

Se trazan paralelas a la última recta recién trazada que pasen por los puntos donde se intersectan los arcos de circunferencia con la recta auxiliar

Dado un segmento \(\overline {AB} \), un punto \(P\) del segmento se dice que divide al segmento \(\overline {AB} \), en la razón \(\frac{{AP}}{{PB}}.\)

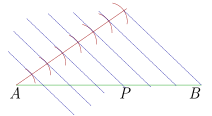
División de un segmento en una razón dada

Dado un segmento \(\overline {AB} \), y dos enteros positivos \(a,b\); se puede encontrar el punto \(P\) que divide al segmento en la razón \(\frac{a}{b};\;\)se puede realizar de la siguiente manera:

1. Se divide el segmento \(\overline {AB} \) en \(a + b\) segmentos de igual longitud.
2. Se toman \(a\) segmentos contando desde el punto \(A\).

Ejemplos

División del segmento \(\overline {AB} \) en la razón \(\frac{a}{b}\)

Razón	Número de partes en que se divide el segmento	Localización del punto \(P\)
\(\frac{{AP}}{{PB}} = \frac{4}{3}\)	\(4 + 3 = 7\)
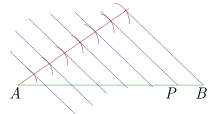\(\frac{{AP}}{{PB}} = 6 = \frac{6}{1}\)	\(6 + 1 = 7\)
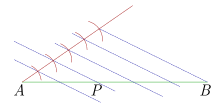\(\frac{{AP}}{{PB}} = \frac{2}{3}\)	\(2 + 3 = 5\)
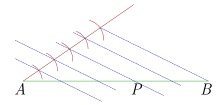\(\frac{{AP}}{{PB}} = \frac{3}{2}\)	\(3 + 2 = 5\)

Ejemplos aplicados del Teorema de Thales

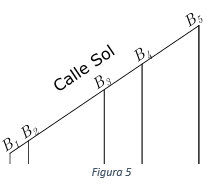
Aplicación 1: Tres solares se extienden desde la calle Sol hasta la calle Luna, como muestra la figura 5.

Los lindes laterales son segmentos perpendiculares a la calle Luna. Si el frente total de los terrenos en la calle Sol mide 120 metros, determine el frente de cada terreno en dicha calle, si además se sabe:

\({A_1}{A_2} = 10{\rm{m}},\;{A_2}{A_3} = 40{\rm{m}},\;{A_3}{A_4} = 20{\rm{m}},\;{A_4}{A_5} = 30{\rm{m}}.\)

Planteamiento del problema

Como las rectas son perpendiculares a la calle Luna entonces son paralelas entre ellas, al aplicar el Teorema de Thales podemos afirmar:

\(\frac{{{A_1}{A_2}}}{{{A_2}{A_3}}} = \frac{{{B_1}{B_2}}}{{{B_2}{B_3}}},\;\;\frac{{{A_1}{A_2}}}{{{A_1}{A_4}}} = \frac{{{B_1}{B_2}}}{{{B_1}{B_4}}}\;,\;\;\frac{{{A_1}{A_2}}}{{{A_1}{A_5}}} = \frac{{{B_1}{B_2}}}{{{B_1}{B_5}}}\)De lo anterior podemos concluir:

\(k = \frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_1}{A_4}}}{{{B_1}{B_4}}} = \frac{{{A_1}{A_5}}}{{{B_1}{B_5}}}\;\)

De manera análoga podemos concluir:

\(k = \frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac{{{A_3}{A_4}}}{{{B_3}{B_4}}} = \frac{{{A_4}{A_5}}}{{{B_4}{B_5}}}\)

Solución

Para determinar la constante de proporcionalidad \(k,\) usaremos propiedades de las proporciones:

\(k = \frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac{{{A_3}{A_4}}}{{{B_3}{B_4}}} = \frac{{{A_4}{A_5}}}{{{B_4}{B_5}}} = \frac{{{A_1}{A_2} + {A_2}{A_3} + {A_3}{A_4} + {A_4}{A_5}}}{{{B_1}{B_2} + {B_2}{B_3} + {B_3}{B_4} + {B_4}{B_5}}} = \frac{{{A_1}{A_5}}}{{{B_1}{B_5}}} = \frac{{100}}{{120}} = \frac{5}{6}\)

De lo anterior obtenemos:
\(\frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{5}{6}\)\(\frac{{{B_1}{B_2}}}{{{A_1}{A_2}}} = \frac{6}{5}\)\({B_1}{B_2} = \frac{6}{5}{A_1}{A_2} = \frac{6}{5}\left( {10} \right) = 12.\)

De manera análoga:

\({B_2}{B_3} = \frac{6}{5}{A_2}{A_3} = \frac{6}{5}\left( {40} \right) = 48\)\({B_3}{B_4} = \frac{6}{5}{A_3}{A_4} = \frac{6}{5}\left( {20} \right) = 24\)\({B_4}{B_5} = \frac{6}{5}{A_4}{A_5} = \frac{6}{5}\left( {30} \right) = 36\)

Respuesta

Segmento	\({B_1}{B_2}\)	\({B_2}{B_3}\)	\({B_3}{B_4}\)	\({B_4}{B_5}\)
Longitud	12m	48m	24m	36m

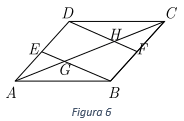
Aplicación 2: Un diseñador gráfico ha diseñado una repisa en forma de paralelogramo y colocará 3 entrepaños como se muestra en la figura 6, los puntos E y F son los puntos medios de los lados \(\overline {AD} \) y \(\overline {BC} ,\) respectivamente. Se tienen que hacer cortes en los entrepaños para poder hacer los ensambles. ¿En qué parte de los entrepaños deben de hacer los cortes?

Planteamiento del problema: Por las condiciones que se dan en el problema se cumple:

\(ED = EA = CF = BF\)

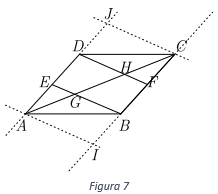
Como construcciones auxiliares extenderemos a los lados \(\overline {CB} \) y \(\overline {DA} \). Por el punto A se traza una recta que pasa por \(A\) y paralela al lado \(\overline {EB} \) y por el punto \(C\;\)se traza una paralela al lado \(\overline {DF} \).

Usaremos el recíproco del Teorema de Thales para demostrar que los segmentos \(\overline {EB} \) y \(\overline {DF} \) son paralelas para poder aplicar el Teorema de Thales.

Solución

Por construcción el cuadrilátero \(EAIB\) es un paralelogramo por lo cual tenemos que EA=BI, por ser lados opuestos de un paralelogramo. Ahora:

\(\frac{{DE}}{{EA}} = \frac{{BF}}{{BI}} = 1\)

Aplicando el recíproco el recíproco del Teorema de Thales podemos concluir:

\(\overline {AI} \parallel \overline {EB} \parallel \overline {DF} \parallel \overline {JC} \)

Tomando a los segmentos \(\overline {AI} \parallel \overline {EB} \parallel \overline {DF} \parallel \overline {JC} \) y a los segmentos BC y CI como sus transversales; como:

\(FC = BF = BI\)\(CH = HG = GA\)

Tomando a \(\overline {AD} \parallel \overline {BC} \) y a los segmentos \(\overline {AC} \) y \(\overline {EB} \) como sus transversales tendremos:

\(\frac{{EG}}{{GB}} = \frac{{AG}}{{GC}} = \frac{{AG}}{{CH + HG}} = \frac{{AG}}{{2\left( {AG} \right)}} = \frac{1}{2}\)

De manera análoga se demuestra que:

\(\frac{{DH}}{{HF}} = 2\)

Respuestas

Los cortes en la diagonal \(\overline {AC} \) se deben hacer en los puntos \(G\;\)y \(H\), tales que:

\(\frac{{AG}}{{AC}} = \frac{{AH}}{{AC}} = \frac{1}{3}\)

Lo mismo sucede para los entrepaños \(\overline {EB} \) y \(\overline {DF} \).