Definición de Velocidad

Ingeniera Industrial, MSc en Física, y EdD
1. Tiempo que utiliza un cuerpo para moverse entre referencias dadas sobre un espacio, y de este modo cambiar su posición, por ejemplo, denotando las marcaciones de salida y llegada, o inicio y fin.
2. Vector de dirección regido por los parámetros de medición del tiempo y la posición, calculado en metro por segundo, pautado universalmente por el Sistema Internacional de Unidades.
3. Característica de rapidez o lentitud manifestada por un ser vivo o una cosa, como una tortuga y un automóvil respectivamente.
4. Capacidad a nivel social en una actividad independientemente de la posición. Ejemplos: velocidad de producción de una fábrica; tiempo de respuesta respecto de un reclamo.
Etimología: Por los modos del latín velocĭtas, velocĭtātis, respecto del adjetivo velox, velōcis, y el sufijo -dad, en la referencia latina -tas, -ātis, en propiedad de cualidad.
Cat. gramatical: Sustantivo fem.
En sílabas: ve-lo-ci-dad.
Velocidad
La velocidad se define como una cantidad vectorial que expresa el cambio de posición de una partícula o cuerpo con respecto al tiempo. Este término resulta de gran uso en el estudio de la cinemática, y es aplicable en casi todas las ramas de la Física, desde la clásica, hasta la moderna.
Velocidad y rapidez media
Por experiencia, asociamos el movimiento de un cuerpo con el término de velocidad, pero el cálculo de esta cantidad física puede hacerse de diferentes maneras. Por ejemplo, la siguiente imagen describe con la línea roja el movimiento unidimensional (r) de una partícula con respecto al tiempo (t). Esta línea no representa la trayectoria, ya que no relaciona dos variables espaciales, sino una variable espacial respecto a la variable temporal.
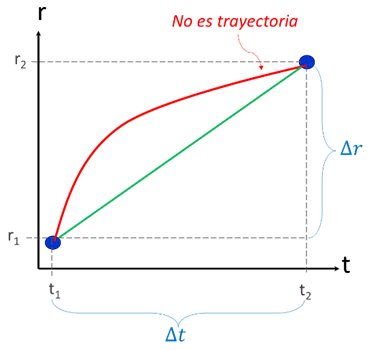
Si consideramos la posición inicial (r1) y final (r2) de la partícula en el intervalo de tiempo en que transcurren ambas posiciones (Δt = t2 – t1), la velocidad media o promedio (vm) será:
\({{\vec{v}}_{m}}=\frac{\Delta \vec{r}}{\Delta t}=\frac{{{{\vec{r}}}_{f}}-{{{\vec{r}}}_{i}}}{{{t}_{f}}-{{t}_{i}}}=\frac{{{{\vec{r}}}_{2}}-{{{\vec{r}}}_{1}}}{{{t}_{2}}-{{t}_{1}}}\)
De esta expresión, se pueden deducir varios aspectos:
o La velocidad media no considera la variación instantánea de la posición en términos del tiempo, ya que solo toma en cuenta la condición inicial y final.
o El numerador de la expresión representa el cambio de posición, es decir, el desplazamiento; por lo tanto, la velocidad media es el desplazamiento del cuerpo entre el intervalo de tiempo.
o La velocidad media es una cantidad que describe la relación entre la dimensión de longitud [L], y la dimensión de tiempo [t], por lo que sus unidades en el Sistema Internacional serán (m/s), en el sistema inglés sería (pies/s), y en general, se expresa como el cociente entre unidades de longitud entre tiempo.
o Al relacionar la expresión de la velocidad media (vm) con el gráfico mostrado, se observa que esta relación representa la pendiente de la recta que va desde el punto inicial de movimiento, hasta el punto final (pendiente de la recta en color verde).
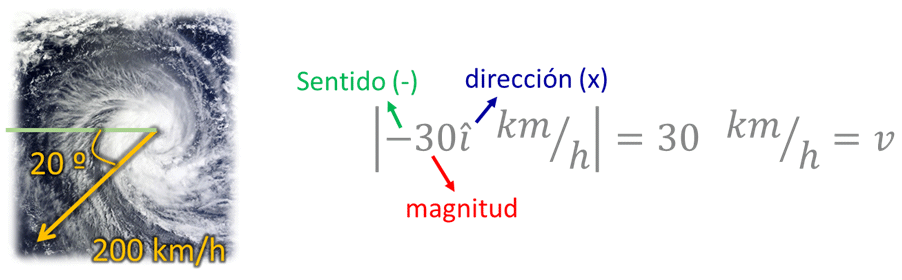
o La velocidad en general, es una cantidad vectorial, por lo tanto, para que esté completamente definida, se requiere expresar su magnitud, dirección y sentido. Por ejemplo, cuando se anuncia un tornado indicando que se viaja a 200 km/h en dirección 20º suroeste, se está indicando la magnitud, dirección y sentido de la velocidad. Si solo se referencia el valor numérico de la velocidad con las unidades, por ejemplo, 30 km/h, se está únicamente haciendo mención a la magnitud de la velocidad.
Rapidez promedio
Así como el desplazamiento de una partícula es diferente a su distancia recorrida, también hay una distinción entre la velocidad media (o promedio) y la rapidez media o (promedio). La primera (vm), expresa el desplazamiento dividido entre el intervalo de tiempo, mientras que la segunda (rm), indica el cociente de la distancia recorrida (d) entre el intervalo de tiempo, es decir, es una cantidad escalar.
\({{r}_{m}}=\frac{d}{\Delta t}\)
Por ejemplo, si un ciclista le da la vuelta a una rotonda que tiene un radio de 10 m en 43 s, el punto inicial A coincide con el punto final B (ya que dio la vuelta completa). En este caso, la distancia recorrida será el perímetro del círculo (d = 2·π·R = 2·π·10 = 62.83 m), mientras que el desplazamiento será 0, por lo tanto:

\({{\vec{v}}_{m}}=\frac{\Delta \vec{r}}{\Delta t}=\frac{{\vec{0}}}{43~s}=\vec{0}\)
\({{r}_{m}}=\frac{d}{\Delta t}=\frac{62.83~m}{43~s}=1.46~{}^{m}\!\!\diagup\!\!{}_{s}\;\)
Nota: solo en trayectorias rectilíneas y unidireccionales, el módulo de la velocidad coincide numéricamente con la rapidez.
Velocidad instantánea
Considerando nuevamente la gráfica inicial, veremos que sucede si calculamos la velocidad media para intervalos de tiempo cada vez más pequeños:
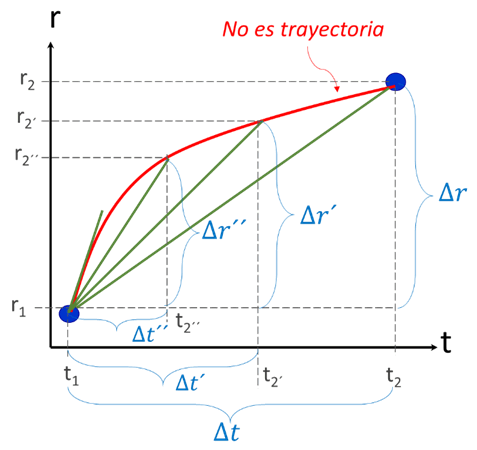
Se puede observar, que a medida que se reduce el intervalo de tiempo, la recta que une a los puntos inicial y final tiende a ser una recta tangente a la curva. Matemáticamente, esto implica evaluar el límite de la velocidad media cuando Δ t → 0.
\(\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \vec{r}}{\Delta t}\)
Este concepto, corresponde a la derivada del desplazamiento con respecto al tiempo.
\(\vec{v}=\frac{d\vec{r}}{dt}\)
Esta nueva expresión se conoce como velocidad instantánea (v), y representa la velocidad de la partícula en un instante particular del tiempo. Asimismo, la interpretación gráfica de una derivada es la pendiente de la recta tangente a una curva, por lo tanto, la velocidad instantánea representa la pendiente de la recta tangente a la curva en un gráfico de posición versus tiempo.
Velocidad angular
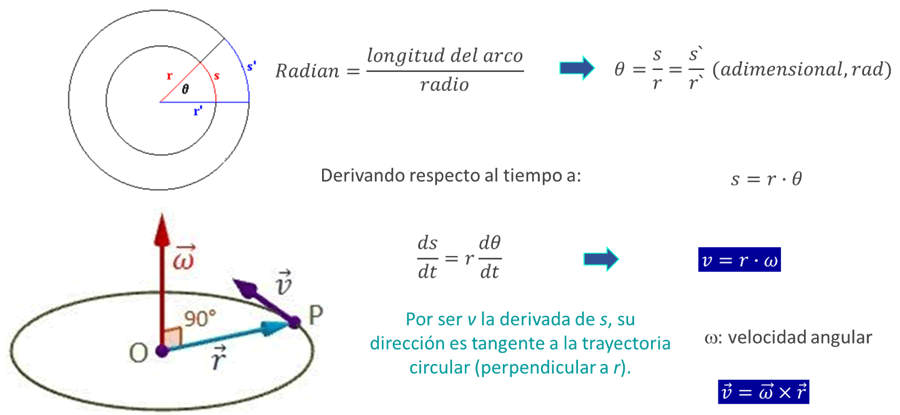
En trayectorias rectilíneas, es común utilizar la velocidad instantánea o lineal para describir el movimiento de un cuerpo, sin embargo, en trayectorias curvilíneas, es de gran utilidad expresar las cantidades en términos angulares, por ejemplo, el ángulo barrido por la partícula, se denomina posición angular θ (rad), la longitud del arco descrito por la trayectoria de la partícula se denomina desplazamiento angular (s), y la posición angular entre el intervalo de tiempo representa la velocidad angular (ω).

Art. actualizado: Junio 2022; sobre el original de diciembre, 2008.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.