Definición de Ángulo

Ingeniera Industrial, MSc en Física, y EdD
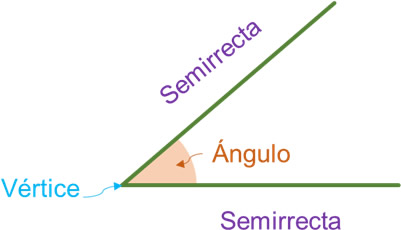
Un ángulo (∠) es una medida utilizada para expresar la inclinación de un plano o recta respecto a un nivel (otro plano o recta) de referencia. Esta medida representa la porción o abertura generada entre dos semirrectas que convergen en un solo punto denominado vértice.
Las dos semirrectas tienen un origen común que representa el vértice. De forma arbitraria, se puede tomar a una de las dos semirrectas como nivel de referencia para expresar el ángulo de la otra semirrecta.
El uso de los ángulos ha hecho posible el diseño y construcción de las obras de ingeniería que se conocen desde hace cientos de años, también ha permitido a los astrónomos comprender y explicar el movimiento de los cuerpos celestes, además, ha sido una gran herramienta para crear arte, ciencia y tecnología.

Desde las construcciones más simples, hasta las más emblemáticas y complejas, han sido posible gracias al uso de ángulos para lograr su diseño.
Los ángulos se expresan en grados, simbolizado con (°), pero también se puede utilizar otro sistema como radianes o el sistema sexagesimal. Sin embargo, cabe destacar que estos no son sistemas de unidades.
Medición de ángulos
Así como existen instrumentos de medición para determinar longitudes, como las reglas o cintas métricas, también hay instrumentos para medir ángulos, denominados transportadores.
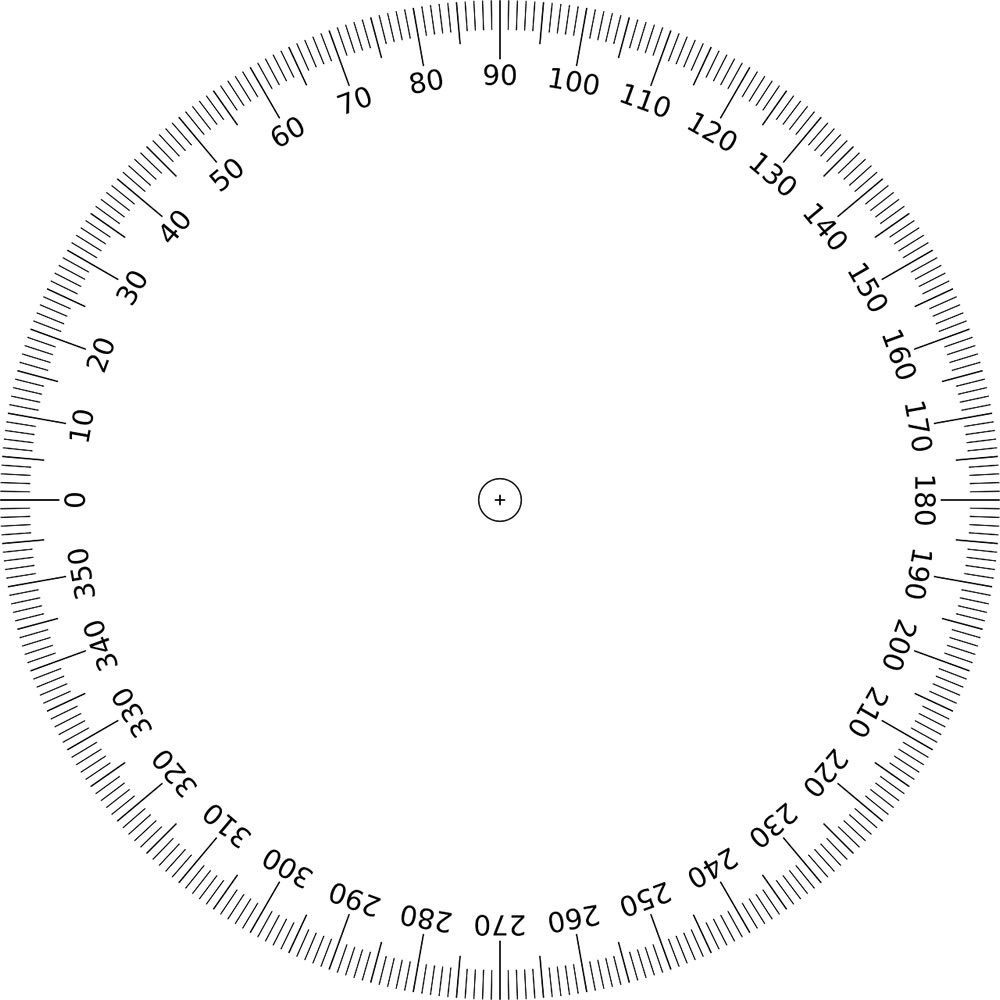
Los transportadores son instrumentos muy sencillos que permiten medir ángulos, desde 0° hasta 360°. También hay modelos que solo abarcan rangos desde 0 a 180°,
Por ejemplo, si se desea determinar el ángulo formado entre dos semirrectas, el procedimiento a aplicar es muy simple:
1. Prologar las dos semirrectas hacia lado donde estas divergen con el propósito de que estas puedan marcar una escala en el transportador.
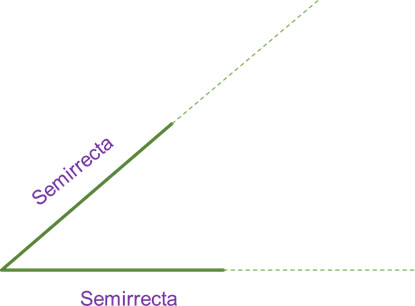
Las líneas segmentadas representan la prolongación de las semirrectas.
2. Colocar el origen del transportador en el vértice donde se ubica el ángulo a medir.
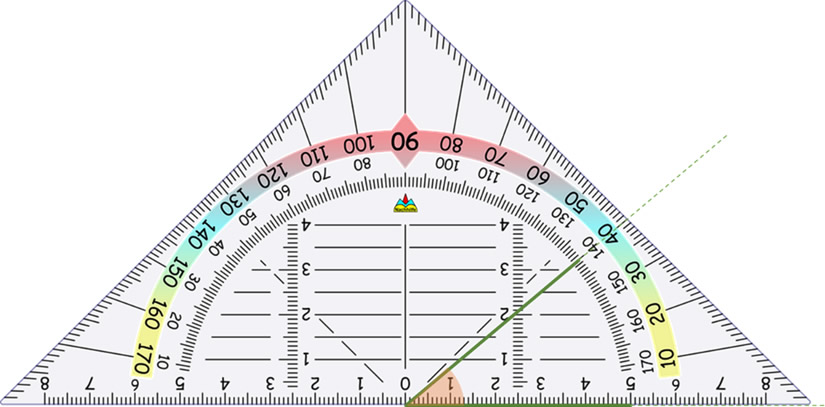
El transportador que se muestra está escalado para medir hasta décimas de grados, desde 0° hasta 180°. El cero de la escala horizontal debe ubicarse en el vértice del ángulo.
3. Tomar la lectura que marca la semirrecta superior, tomando la lectura desde la semirrecta horizontal (0°), hasta la semirrecta superior medida en sentido antihorario.
4. Finalmente, la lectura registrada por el transportador representa la medida del ángulo, en este caso, 40°.
Clasificación de los ángulos
Existen diferentes criterios para clasificar los ángulos, por ejemplo, de acuerdo a su valor, o por su posición. A continuación, se describen los diferentes tipos de ángulos.
De acuerdo con su valor numérico, un ángulo puede ser:
Agudo: son los ángulos cuyas medidas se encuentran mayores a 0° y menores a 90° (0° < agudo < 90°).
Nulo: es un ángulo que mide exactamente 0°.
Recto: es un ángulo que mide exactamente 90°. Se simboliza con un pequeño cuadro en el vértice donde se encuentra dicho ángulo.
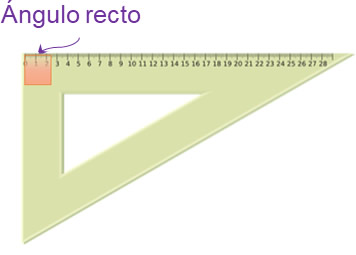
La presencia de un ángulo recto en un triángulo lo clasifica como triángulo rectángulo, el cual es una figura base para el teorema de Pitágoras y trigonometría.
Obtuso: es un ángulo cuya medida es mayor de 90° y menor de 180° (90° < ∠ obtuso < 180°).
Llano: son los ángulos que miden exactamente 180°.
Completo: es un ángulo que mide 360°
Considerando su posición, los ángulos se clasifican en:
Adyacentes: se refiere a dos ángulos que tienen el vértice y un lado en común. La suma de dos ángulos adyacentes es igual a 180°.
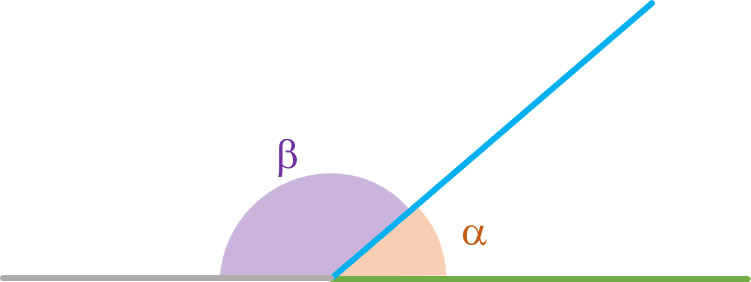
Los ángulos mostrados son adyacentes, por lo tanto, la suma de ellos forma un ángulo llano.
Los ángulos que forman ángulos adyacentes también se denominan suplementarios.
Consecutivos: son los ángulos que tienen el vértice y un lado en común, pero a diferencia de los ángulos adyacentes, forman ángulos diferentes a 180°.
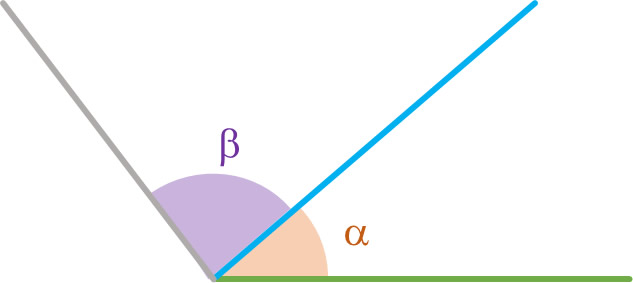
Los ángulos α y β son consecutivos.
Si dos ángulos consecutivos suman 90° se denominan complementarios.
Si dos ángulos tienen el mismo valor, se dice que son congruentes.
Ángulos entre paralelas
Si se trazan dos rectas paralelas (tienen la misma inclinación) y ambas son cortadas por una secante, formarán ángulos internos y externos.
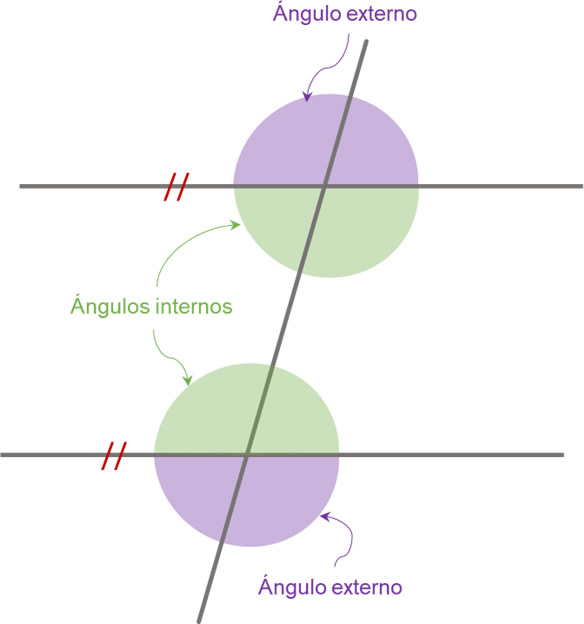
La correcta identificación de los ángulos internos y externos es de gran importancia, ya que a partir de ellos se pueden aplicar criterios de congruencia.
Para los ángulos formados entre dos rectas paralelas que se cortan por una secante, se generan los siguientes ángulos congruentes:
• Alternos internos.
• Alternos externos.
• Opuestos por el vértice.
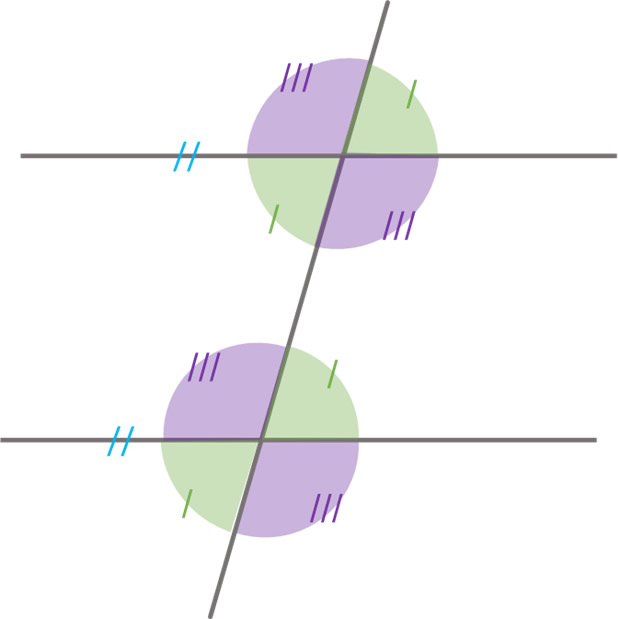
La imagen muestra con colores y marcas los ángulos congruentes formados al cortar con una recta secante dos rectas paralelas.
Sistema sexagesimal
Existen diversos sistemas de numeración decimal, uno de los cuales permite expresar ángulos y tiempo al dividir un grado en 60 partes. Para ello, se aplican las conversiones de tiempo:
• 1 minuto = 1’
• 1 segundo = 1’’
• 1° = 60’
• 1’ = 60’’ (1 minuto = 60 segundos)
• 1° = 3,600’’
Comúnmente, se suelen utilizar estas conversiones para expresar la parte decimal de la medida de un ángulo en minutos y segundos, por ejemplo, 37.46° equivale a:
• La parte entera queda igual (en grados):
37°,x’,x’’
• La parte decimal de los grados se transforma a minutos (1° = 60’):
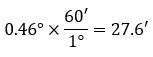
• La parte decimal de los minutos se convierte a segundos (1’ = 60’’):
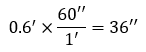
El resultado final es:
37.46° = 37°27’36’’

Art. actualizado: Dic. 2022; sobre el original de julio, 2009.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.