¿Qué es la Ecuación de Dirac, y cómo se define?

Ingeniera Industrial, MSc en Física, y EdD
Paul Adrien Maurice Dirac (1902-1984) propuso a finales de 1928 una de las ecuaciones con mayor trascendencia e implicaciones en la Física de la era actual, y esto se debe a que unifica los principios de la mecánica cuántica con los de la relatividad.
Esta ecuación se puede expresar de varias maneras, siendo la más compacta y simplificada la que es considerada como una de las ecuaciones más estéticas de la ciencia:
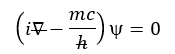
Donde:
i: unidad imaginaria
m: masa en reposo del electrón
ħ: constante reducida de Planck
c: velocidad de la luz
/∇: operador de sumatoria de derivadas parciales
ψ: función matemática de onda del electrón
El valor absoluto del cuadrado de la función de onda representa la probabilidad de encontrar a la partícula en una determinada posición, considerando su energía, velocidad, entre otros parámetros, así como su evolución en el tiempo. En otras palabras, la ecuación de Paul Dirac utiliza matrices actuando sobre vectores y representa una evolución de la ecuación de Schrödinger en una Física cuántica relativista.
La ecuación de Dirac, en principio, se utilizó para describir el comportamiento de un electrón desprovisto de interacción, aunque su aplicabilidad se extiende a la descripción de partículas subatómicas cuando viajan a velocidades próximas a la de la luz. Dirac logró explicar a escala subatómica el comportamiento dual de onda y partícula que ya se conocía en ese momento, ya que consideró las propiedades de las partículas como el momento angular intrínseco o espín.
Otro de los significativos aportes de la ecuación de Dirac es la predicción de antimateria, cuya existencia fue posteriormente demostrada (en 1932) por Carl D. Anderson utilizando una cámara de niebla con la cual identificó el positrón. Asimismo, explica en gran medida la estructura fina identificada en las líneas espectrales atómicas.
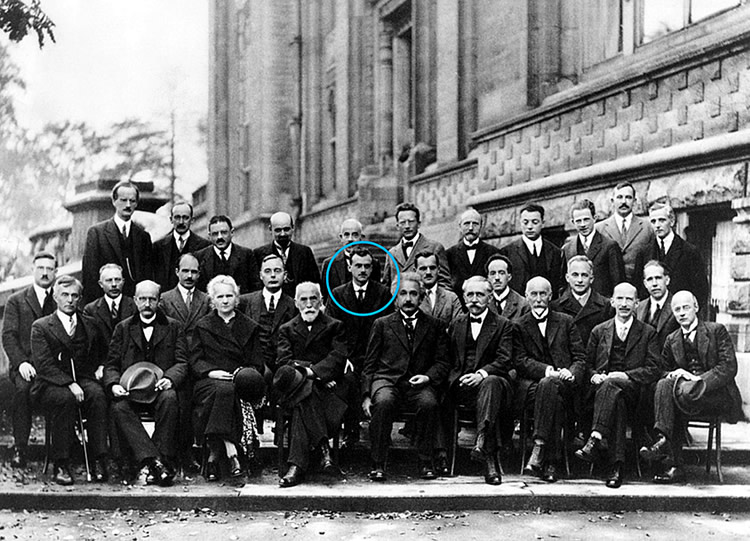
La imagen muestra la famosa fotografía tomada durante la conferencia “Fotones y electrones” en 1927 donde se retratan a algunos de los científicos más destacados de la historia. En la circunferencia celeste se encuentra Paul Dirac.
Bases para la ecuación de Dirac
A fin de entender las consideraciones tomadas por Dirac en el desarrollo de su ecuación, así como las bases en las que se fundamentó su planteamiento, es importante conocer las teorías previas a su modelo.
En primer lugar, está la famosa ecuación de Schrödinger de la mecánica cuántica, publicada en 1925, la cual convierte las magnitudes en operadores cuánticos. Esta ecuación utiliza la función de onda (ψ), tomando como punto de partida la ecuación clásica de la energía E = p2/2m y le incorpora las reglas de cuantización tanto al momentum (p), como a la energía (E):
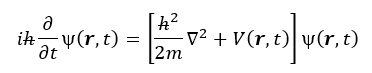
La derivada parcial ∂/∂t expresa la evolución del sistema respecto al tiempo. Mientras el segundo término se relaciona con la energía potencial, el primer término dentro del corchete hace referencia a la energía cinética:
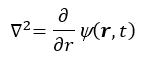
Nota: en la teoría de la relatividad de Einstein, las variables de espacio y tiempo, deben entrar de manera equiparable en las ecuaciones, lo cual no ocurre en la ecuación de Schrödinger, en la cual el tiempo aparece como una derivada, y la posición como una segunda derivada.
Ahora bien, desde hace siglos, los científicos han tratado de hallar un modelo de la Física que unifique las diferentes teorías, y en el caso de la ecuación de Schrödinger, toma en cuenta la masa (m) y la carga del electrón, pero no considera los efectos relativistas que se manifiestan a altas velocidades. Por esta razón, en el año de 1926, los científicos Oskar Klein y Walter Gordon, proponen una ecuación que sí toma en cuenta los principios de la relatividad:
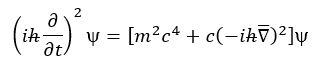
El problema de la ecuación de Klein – Gordon es que se basa en la de Einstein, en la cual la energía está al cuadrado, por lo que esta ecuación (Klein – Gordon) incorpora una derivada al cuadrado respecto al tiempo, y esto implica que posee dos soluciones, dando cabida a valores negativos del tiempo, y esto carece de sentido físico. Asimismo, tiene el inconveniente de generar como soluciones valores de probabilidades menores que cero.
Tratando de resolver las inconsistencias que implicaban las soluciones negativas de ciertas magnitudes que no admiten estos resultados, Paul Dirac partió de la ecuación de Klein – Gordon para linealizarla, y en este procedimiento, introdujo dos parámetros en forma de matrices de dimensión 4, conocidas como matrices de Dirac o también de Pauli, y que son una representación del álgebra del espín. Estos parámetros están denotados como α y β` (en la ecuación de energía, se representan como E = α⋅pc + β⋅mc2):
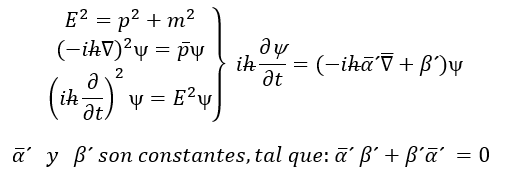
Para que esta igualdad se cumpla, la condición es que β´2 = m2c4
Por lo general, las reglas de cuantización conllevan a operaciones con derivadas que aplican a funciones de onda escalar, sin embargo, como los parámetros α y β son matrices de 4×4, los operadores diferenciales intervienen sobre un vector de cuatro dimensiones (ψ), conocido como espinor.
La ecuación Dirac resuelve el problema de la energía negativa que se presentaba en la ecuación de Klein – Gordon, pero sigue apareciendo una solución con energía negativa; es decir, unas partículas con propiedades análogas a las de la otra solución pero con carga opuesta, a esto, Dirac lo denominó antipartículas. Además, con la ecuación de Dirac, se demuestra que el espín es el resultado de aplicar las propiedades relativistas al mundo cuántico.

Trabajo publicado en: Ago., 2022.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.