Significado de fuerza centrífuga y centrípeta Definición, diferencia, y ejercicios

Licenciada en Física
Definición formal
La fuerza centrífuga y centrípeta son partícipes del movimiento circular, cuya diferencia principal radica en el marco de referencia desde el que se analiza el movimiento. Se habla de fuerza centrífuga (fuerza hacia afuera) cuando se examina el movimiento desde el marco de referencia fijo en el objeto que da vueltas, mientras que la fuerza centrípeta es la responsable de mantener al objeto dando vueltas, visto desde un sistema de referencia fijo en Tierra.
A la fuerza centrífuga se la conoce como pseudo-fuerza o fuerza ficticia, porque no es el resultado de una interacción verdadera entre dos objetos, aunque sea muy real para los ocupantes de un automóvil que está dando una curva, sobre todo si van a buena velocidad. Los pasajeros sienten que algo invisible los empuja hacia afuera, de allí la denominación de fuerza centrífuga, pero en realidad lo que sienten las personas es la inercia que todos los cuerpos poseen: la resistencia natural a cambiar el movimiento. No es posible identificar al agente responsable de “echar fuera” a los pasajeros y por eso la fuerza centrífuga es una fuerza ficticia.
En cambio, la fuerza centrípeta, vista desde un marco de referencia fijo en la Tierra, claramente es la que ayuda al objeto a permanecer en su trayectoria, apuntando hacia el centro de la circunferencia. Sin ella el movimiento circular no es posible.
El observador en dicho marco puede identificar fácilmente a la fuerza responsable, por ejemplo, cuando un niño juega haciendo girar una piedra atada a una cuerda, la fuerza que mantiene la rotación proviene de la tensión. Si esta tensión desaparece súbitamente, bien sea porque el niño afloje la cuerda o esta se reviente, la piedra de inmediato deja de dar vueltas, y en caso de ruptura, la piedra describe un arco de parábola (porque quedó librada a la gravedad) y va a parar al suelo.
No solamente la tensión puede hacer de fuerza centrípeta, también están otras interacciones conocidas. La gravedad, el rozamiento, la atracción electrostática o la fuerza magnética, a veces se ocupan de hacer que los objetos o las partículas se mantengan en rotación y en ese caso, dichas fuerzas se dirigen siempre hacia el centro de la circunferencia descrita.
Sistemas de referencia: inercial, y no inercial
De todo lo antes dicho, se concluye que el marco de referencia seleccionado para observar el movimiento influye mucho en la manera en que un observador describe las cosas.
Para empezar, hay que distinguir los dos tipos de marco de referencia. El que está fijo a Tierra se llama marco de referencia inercial, mientras que el que acompaña al objeto que rota es un marco de referencia no inercial.
El primero se supone que no está acelerado (no considera el movimiento de rotación terrestre) y el segundo sí, porque para dar vueltas se necesita una aceleración centrípeta, ya que la velocidad se ve obligada a cambiar continuamente de dirección.
La fuerza centrífuga nunca aparece ante la vista del observador ubicado en el sistema de referencia inercial. Este jamás ve que el objeto sea empujado hacia fuera de la trayectoria, por el contrario, para él, la fuerza que mantiene el movimiento siempre está dirigida hacia el centro.
Ahora bien, resulta que la segunda ley de Newton es válida únicamente para los sistemas de referencia inerciales. Entonces, ¿qué fuerzas actúan sobre el automóvil que da la curva a gran velocidad, según un observador que lo ve todo estando de pie en la acera?
Este observador externo advierte que la interacción que suministra al automóvil la fuerza dirigida hacia el centro de la curva es la fricción entre los neumáticos y el pavimento. Y directamente sobre los pasajeros, nota que existe la normal que ejerce la portezuela o la curvatura de la butaca, obligándolos a seguir la circunferencia.
Ejercicios
Ejercicio 1
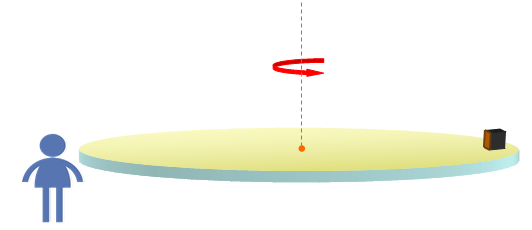
Un bloquecito de masa m se encuentra en el borde de una plataforma giratoria como se muestra en la figura. Hay rozamiento entre las superficies. ¿Cómo dibujaría el observador parado enfrente de la plataforma el diagrama de cuerpo libre del bloquecito?
Respuesta
Un diagrama de cuerpo libre es un esquema donde aparecen todas las fuerzas que actúan sobre el objeto.
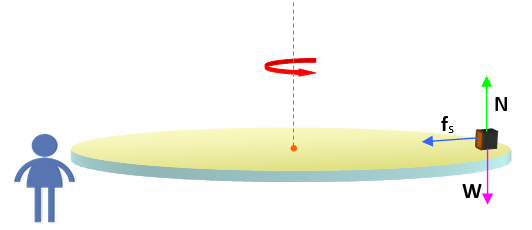
El observador frente a la plataforma es un observador inercial e identifica de inmediato la fuerza centrípeta, dirigida hacia el centro de la trayectoria, como el roce estático fs entre el bloquecito y la plataforma.
Además observa la normal N que ejerce la plataforma y el peso W, ambas fuerzas verticales se equilibran, por lo tanto la aceleración vertical es 0. Como el observador sabe que está en un sistema inercial, aplica la segunda ley de Newton de esta manera:
∑ Fy = N−W = 0
Y en la dirección radial, el observador se da cuenta de que hay una fuerza dirigida hacia el centro y escribe:
∑ Fr = fs = m∙ac
Donde el rozamiento estático fs es la fuerza que interpreta el rol de la fuerza centrípeta, y ac es la aceleración, también centrípeta.
Ejercicio 2
¿Cómo sería el diagrama de cuerpo libre de un observador que viajara sobre el bloquecito?
Respuesta
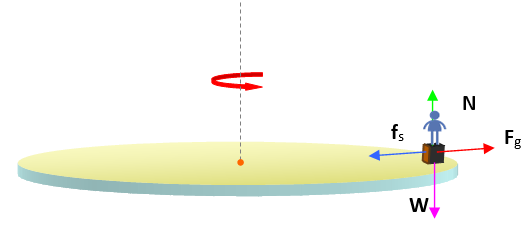
Respecto al marco de referencia fijo al bloquecito, el observador ve que este se encuentra quieto, y por lo tanto asegura que las fuerzas sobre él se equilibran.
El observador afirma que en sentido vertical la normal N equilibra al peso W, y en sentido radial, el roce fs se equilibra con la fuerza ficticia Fg (él no identifica al agente que la causa, por eso es ficticia) y la llama fuerza centrífuga porque su efecto es echar al bloquecito fuera de la plataforma.
Como el observador no percibe aceleración, escribe:
∑ Fy = N−W = 0
∑ Fr = fs−Fg = 0

Trabajo publicado en: Nov., 2020.